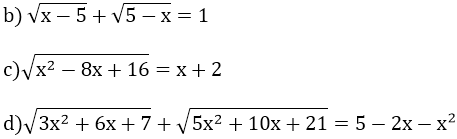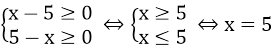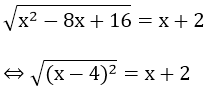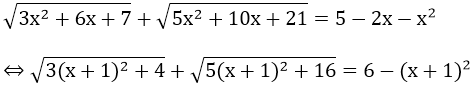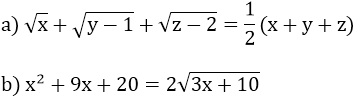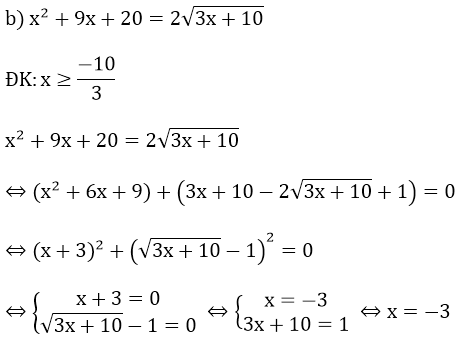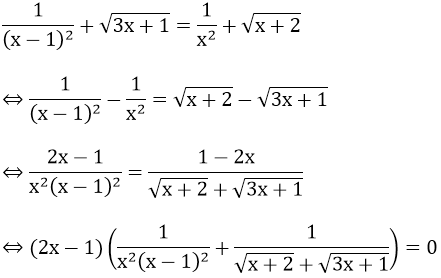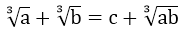Cách giải phương trình chứa dấu căn cực hay, có đáp án

Lý thuyết và Phương pháp giải

    Phương trình chứa ẩn dưới dấu căn có nhiều cách giải, sau đây là một số phương pháp thường dùng:

        + Nâng lên lũy thừa

        + Đặt ẩn phụ

        + Đưa về phương trình chứa dấu giá trị tuyệt đối

        + Sử dụng bất đẳng thức, đánh giá hai vế của phương trình

Ví dụ minh họa

Ví dụ 1: Giải các phương trình sau:

    a) (√x - 2)(5 - √x) = 4 - x

Hướng dẫn:

    a) Dạng 1: Đưa phương trình đã cho về phương trình tích

    ĐK: x ≥ 0

    (√x - 2)(5 - √x) = 4 - x

    ⇔ (√x - 2)(5 - √x) = (2 - √x)(2 + √x)

    ⇔ (√x - 2)(5 - √x + 2 + √x) = 0

    ⇔ 7(√x - 2) = 0

    ⇔ √x - 2 = 0 ⇔ x = 4

    Vậy phương trình có nghiệm duy nhất x = 4

    b) Dạng 2: Đánh giá điều kiện của phương trình.

    ĐK: 

    Thay x = 5 vào phương trình thấy không thỏa mãn

    Vậy phương trình vô nghiệm

    c) Dạng 3: Đưa về phương trình chứa dấu giá trị tuyệt đối

    ⇔ |x - 4| = x + 2

    Vậy phương trình có nghiệm x = 1

    d) Dạng 4: Đánh giá 2 vế của phương trình.

    Vế trái của phương trình 

    Vế phải của phương trình 6 - (x + 1)² ≤ 6

    Đẳng thức chỉ xảy ra khi x = -1

    Vậy phương trình có nghiệm duy nhất x = -1

Ví dụ 2: Giải các phương trình sau:

    Chú ý: Các phương trình trên đều quy về phương trình dạng:

    A + B + C = 0 (*)

    Trong đó: A, B, C ≥ 0 nên phương trình (*) ⇔ A = B = C = 0.

Hướng dẫn:

    ĐK: x ≥ 0; y ≥ 1; z ≥ 2

    Phương trình tương đương với:

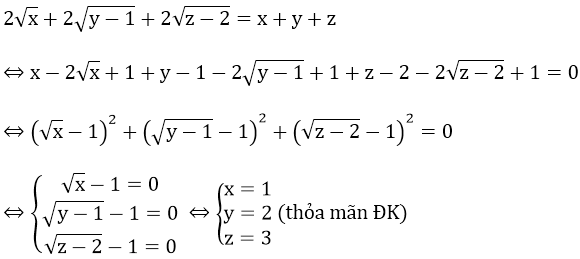
    Vậy phương trình có nghiệm x = -3.

Ví dụ 3: Giải phương trình sau:

Hướng dẫn:

    ĐK: x ≠ 0; x ≠ 1; x ≥ (-1)/3

    Do  ∀x thỏa mãn ĐK nên

    2x - 1 = 0 ⇔ x = 1/2 (TMĐK)

    Vậy phương trình có nghiệm x = 1/2

Ví dụ 4: Giải phương trình sau:

    Phương pháp giải: Phương trình có dạng: 

    Dùng phương pháp đặt ẩn phụ, đưa về: m + n = c + mn.

Hướng dẫn:

    Đặt

    Phương trình có dạng: a + b = 1 + ab

    ⇔ a - 1 + b - ab = 0

    ⇔ a - 1 + b(1 - a) = 0

    ⇔ (a - 1)(1 - b) = 0