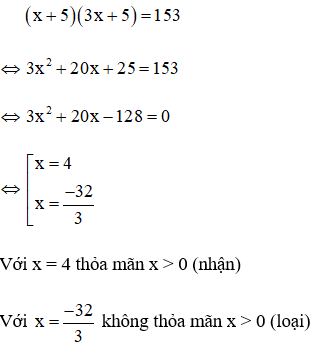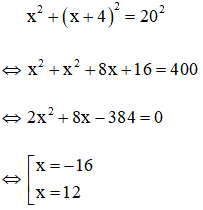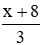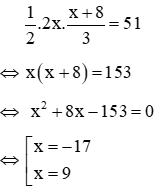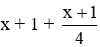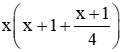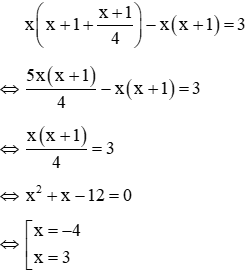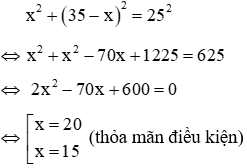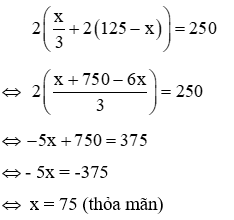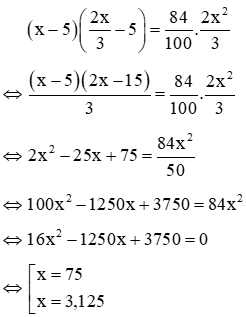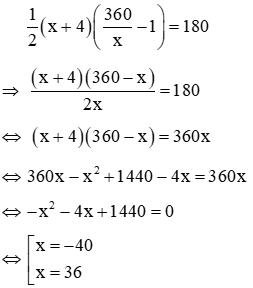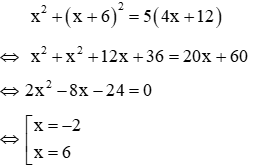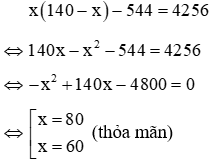Giải bài toán bằng cách lập phương trình – Dạng hình học

A. Phương pháp giải

B1: Lập phương trình

- Chọn ẩn số và đặt điều kiện cho ẩn

- Biểu diễn các dữ kiện chưa biết qua ẩn số

- Lập phương trình biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Một số lưu ý:

- Nếu hình chữ nhật có 2 cạnh là a và b thì diện tích của hình chữ nhật là a.b,

chu vi của hình chữ nhật là 2(a + b)

- Nếu hình vuông có cạnh bằng a thì diện tích hình vuông là a², chu vi của hình vuông là 4a

- Chu vi tam giác bằng tổng độ dài 3 cạnh, diện tích tam giác bằng một nửa tích độ dài đường cao nhân cạnh đáy tương ứng

- Nếu tam giác vuông có 2 cạnh góc vuông là a và b, cạnh huyền là c thì

c² = a² + b² (Định lý Pi-ta-go)

Ví dụ 1: Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm 5cm thì được một hình chữ nhật mới có diện tích bằng 153cm². Tính chu vi của hình chữ nhật ban đầu

Giải

Gọi chiều rộng của hình chữ nhật là x cm (x > 0)

⇒ chiều dài của hình chữ nhật là 3x (cm)

Chiều rộng tăng thêm 5cm thì có độ dài mới là x + 5 (cm)

Chiều dài tăng thêm 5cm thì có độ dài mới là 3x + 5 (cm)

Vì diện tích hình chữ nhật mới là 153cm² nên ta có phương trình:

Vậy hình chữ nhật ban đầu có chiều rộng là 4cm, chiều dài là 12cm. Do đó chu vi của hình chữ nhật ban đầu là: 2(4 + 12) = 32 (cm)

Ví dụ 2: Cho tam giác vuông có cạnh huyền bằng 20cm. Hai cạnh góc vuông có độ dài hơn kém nhau 4cm. Tính độ dài hai cạnh góc vuông của tam giác vuông

Giải

Gọi một cạnh góc vuông của tam giác là x cm (x > 0)

⇒ cạnh góc vuông còn lại của tam giác là x + 4 (cm)

Vì cạnh huyền của tam giác bằng 20cm nên theo định lý Pitago ta có phương trình

Với x = -16 không thỏa mãn x > 0 (loại)

Với x = 12 thỏa mãn x > 0 (nhận)

Vậy một cạnh góc vuông là 12cm, cạnh còn lại 16cm

B. Bài tập

Câu 1: Một tam giác vuông có 2 cạnh góc vuông hơn kém nhau 8m. Nếu tăng một cạnh góc vuông lên 2 lần và giảm một cạnh góc vuông đi 3 lần thì được tam giác mới có diện tích 51m². Tính độ dài hai cạnh góc vuông

A. 8m và 16m

B. 9m và 17m

C. 10m và 18m

D. 11m và 19m

Giải

Gọi độ dài một cạnh góc vuông là x(m), x > 0

⇒ cạnh góc vuông còn lại là x + 8

Giả sử tăng cạnh nhỏ lên 2 lần thì độ dài cạnh nhỏ là 2x

Giảm cạnh lớn đi 3 lần thì độ dài cạnh lớn là 

Vì tam giác mới có diện tích 51m² nên ta có phương trình

Ta thấy x = -17 < 0 (loại), x = 9 > 0(nhận)

Vậy tam giác vuông có một cạnh góc vuông bằng 9m, cạnh còn lại là 17m

Đáp án là B

Câu 2: Một hình chữ nhật có chiều rộng ngắn hơn chiều dài 1m. Nếu chiều dài tăng thêm 1/4 lần độ dài của nó thì được một hình chữ nhật mới có diện tích tăng thêm 3m². Tính diện tích của hình chữ nhật ban đầu

A. 12m²

B. 13m²

C. 14m²

D. 15m²

Giải

Gọi chiều rộng của hình chữ nhật là x(m), x > 0

chiều dài của hình chữ nhật là x + 1 (m)

Chiều dài tăng thêm 1/4 lần độ dài của nó thì có độ dài mới là 

Diện tích của hình chữ nhật ban đầu là: x(x + 1)

Diện tích hình chữ nhật mới là 

Vì diện tích hình chữ nhật mới hơn diện tích của hình chữ nhật ban đầu 3m² nên ta có phương trình

Với x = 3 thỏa mãn x > 0 (nhận)

Với x = -4 không thỏa mãn x > 0 (loại)

Vậy hình chữ nhật ban đầu có chiều rộng là 3m, chiều dài là 4m. Do đó diện tích của hình chữ nhật ban đầu là: 3.4 = 12 (m²)

Đáp án là A

Câu 3: Một tam giác vuông có chu vi là 60m và có cạnh huyền là 25m. Tính độ dài hai cạnh góc vuông của tam giác.

A. 28m và 7m

B. 18m và 17m

C. 30m và 5m

D. 20m và 15m

Giải

Tổng hai cạnh góc vuông bằng 60 – 25 = 35(m)

Gọi độ dài một canh góc vuông là x(m), 35 > x > 0

⇒ cạnh góc vuông còn lại là 35 - x

Áp dụng Pitago cho tam giác ta có phương trình:

Vậy tam giác vuông có một cạnh góc vuông bằng 20m, cạnh còn lại là 15m

Đáp án là D

Câu 4: Một khu vườn hình chữ nhật có chu vi là 250m. Tính diện tích của khu vườn biết rằng nếu một cạnh giảm 3 lần và cạnh còn lại tăng 2 lần thì chu vi của khu vườn không đổi

A. 3720m²

B. 3730m²

C. 3740m²

D. 3750m²

Giải

Nửa chu vi của khu vườn là 250 : 2 = 125(m)

Gọi cạnh thứ nhất của khu vườn là: x (m), 0 < x < 125

⇒ cạnh thứ hai của khu vườn là: 125 – x (m)

Giả sử cạnh thứ nhất giảm đi 3 lần thì độ dài cạnh thứ nhất bằng 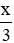 (m)

Giả sử cạnh thứ hai tăng lên 2 lần thì độ dài cạnh thứ hai bằng 2(125 – x) (m)

Vì khi một cạnh giảm 3 lần và cạnh còn lại tăng 2 lần thì chu vi của khu vườn không đổi nên ta có phương trình

Vậy một cạnh của khu vườn bằng 75m, cạnh còn lại là 50m. Do đó diện tích của khu vườn hình chữ nhật ban đầu là: 75 × 50 = 3750(m²)

Đáp án là D

Câu 5: Một hình chữ nhật có cạnh này bằng 2/3 cạnh kia. Nếu bớt đi mỗi cạnh 5m thì diện tích của hình chữ nhật giảm đi 16%. Tính các kích thước của hình chữ nhật ban đầu

A. 75m và 50m

B. 60m và 40m

C. 30m và 20m

D. 45m và 30m

Giải

Gọi một cạnh của hình chữ nhật là x(m), x > 5

Vì diện tích hình chữ nhật mới giảm đi 16% nghĩa là chỉ bằng 84% diện tích của hình chữ nhật ban đầu nên ta có phương trình

Với x = 3,125 không thỏa mãn x > 5 (loại)

Với thỏa mãn x > 5 (nhận)

Vậy hình chữ nhật ban đầu có một cạnh là 75m, cạnh còn lại là 50m.

Đáp án là A

Câu 6: Một thửa ruộng tam giác có diện tích 180m². Tính chiều dài cạnh đáy thửa ruộng, biết rằng nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm đi 1m thì diện tích không đổi

A. 10m

B. 35m

C. 36m

D. 18m

Giải

Gọi cạnh đáy của thửa ruộng là x(m), x > 0

Từ công thức tính diện tích tam giác ta có chiều cao của thửa ruộng là 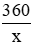 (m)

Cạnh đáy tăng lên 4m thì có độ dài mới là x + 4(m)

Chiều cao giảm đi 1m thì có độ dài mới là 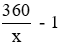 (m)

Vì sau khi cạnh đáy tăng lên 4m và chiều cao tương ứng giảm đi 1m thì diện tích không đổi nên ta có phương trình

Ta thấy x = -40 < 0 (loại), x = 36 > 0 (nhận)

Vậy cạnh đáy của thửa ruộng là 36m

Đáp án là C

Câu 7: Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 6m và bình phương đường chéo gấp 5 lần chu vi. Tính chiều dài và chiều rộng của hình chữ nhật

A. 6m và 12m

B. 7m và 13m

C. 8m và 14m

D. 9m và 15m

Giải

Gọi chiều rộng của hình chữ nhật là x(m), x > 0

⇒ chiều dài của hình chữ nhật là x + 6

Chu vi của hình chữ nhật là: 2(x + x + 6) = 4x + 12

Bình phương độ dài đường chéo là: x² + (x + 6)²

Vì bình phương đường chéo gấp 5 lần chu vi nên ta có phương trình

Ta thấy x = -2 < 0 (loại), x = 6 > 0 (nhận)

Vậy chiều rộng bằng 6m, chiều dài bằng 12m

Đáp án là A

Câu 8: Một khu vườn hình chữ nhật có chu vi là 280m. Người ta làm lối đi xung quanh vườn (thuộc đất trong vườn) rộng 2m. Tính kích thước của vườn, biết rằng đất còn lại trong vườn để trồng trọt là 4256m².

A. 70m và 70m

B. 60m và 80m

C. 30m và 110m

D. 50m và 90m

Giải

Nửa chu vi của khu vườn là 280 : 2 = 140(m)

Gọi một cạnh của khu vườn là: x(m), 4 < x < 140

⇒ cạnh còn lại của khu vườn là: 140 – x (m)

Diện tích của toàn bộ khu vườn là: x(140 – x)

Diện tích để làm lối đi là: 4(x – 4) + 4(140 – x) = 544(m²)

Vì diện tích đất còn lại để trồng cây là 4256m² nên ta có phương trình

Vậy khu vườn có một cạnh là 80m, cạnh còn lại là 60m.

Đáp án là B