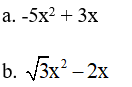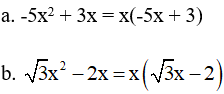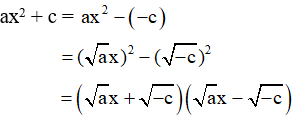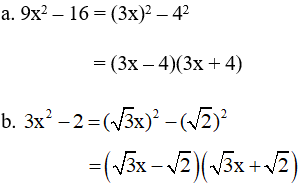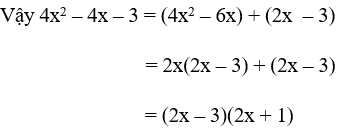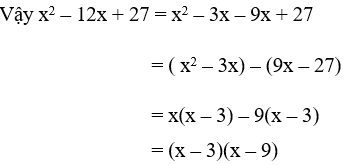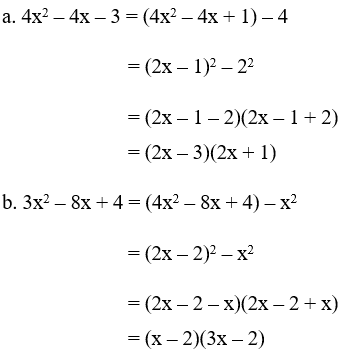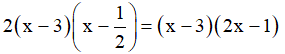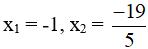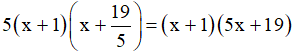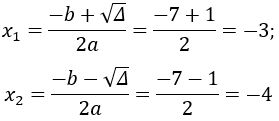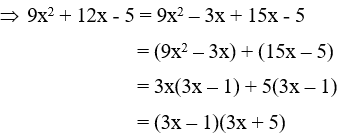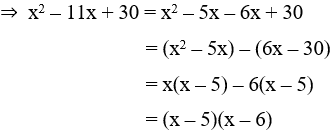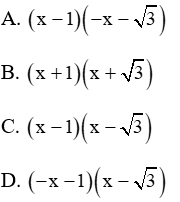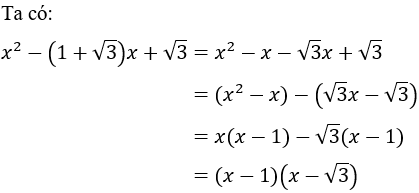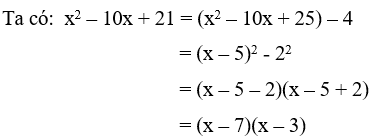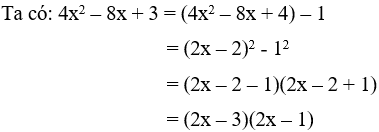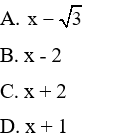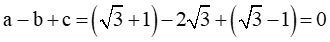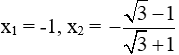Cách phân tích đa thức ax² + bx + c thành nhân tử để giải phương trình bậc hai

A. Phương pháp giải

Cách 1: Đặt nhân tử chung

- Sử dụng trong trường hợp c = 0, khi đó ta có ax² + bx = x(ax + b)

Ví dụ: Phân tích biểu thức sau thành nhân tử

Giải

Cách 2: Dùng hằng đẳng thức A² – B²

- Sử dụng trong trường hợp b = 0 và c < 0, khi đó ta có:

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 9x² – 16

b. 3x² – 2

Giải

Cách 3: Tách số hạng bx thành hai số hạng rồi nhóm các hạng tử và đặt nhân tử chung

-bổ sung- Để tách bx thành hai hạng tử ta làm như sau:

+ B1: Tìm tích ac, phân tích ac thành tích hai thừa số nguyên

+ B2: Chọn hai thừa số có tổng bằng b

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 4x² – 4x - 3

b. x² – 12x + 27

Giải

a. Tích ac = -12 = (-1).12 = (-12).1 = 2.(-6) = (-2).6

Trong các cặp số trên ta chọn cặp số 2 và -6 vì tổng của chúng bằng -4 = b

⇒ -4x = -6x + 2x

b. Tích ac = 27 = 1.27 = (-1).(-27) = 3.9 = (-3).(-9)

Trong các cặp số trên ta chọn cặp số -3 và -9 vì tổng của chúng bằng -12 = b

⇒ -12x = -3x - 9x

Cách 4: Tách số hạng (ax² hoặc c) thành hai số hạng rồi đưa biểu thức

ax² + bx +c về dạng A² – B²

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 4x² – 4x – 3

b. 3x² – 8x + 4

Giải

Cách 5: Sử dụng nghiệm của phương trình bậc hai

- Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì:

ax² + bx + c = a(x – x₁)(x – x₂)

Ví dụ: Phân tích biểu thức sau thành nhân tử

a. 2x² – 7x + 3

b. 5x² + 24x + 19

Giải

a. Xét phương trình 2x² – 7x + 3 = 0 có: Δ = b² - 4ac = (-7)² - 4.2.3 = 25 > 0

Do đó phương trình có 2 nghiệm phân biệt: x₁ = 3, x₂ = 1/2

Vậy 2x² – 7x + 3 = 

b. Xét phương trình 5x² + 24x + 19 = 0 có: Δ = b² - 4ac = (24)² - 4.5.19 = 196 > 0

Do đó phương trình có 2 nghiệm phân biệt: x₁ = -1, x₂ = 

Vậy 5x² + 24x + 19 = 

B. Bài tập

Câu 1: Kết quả phân tích biểu thức x² + 7x + 12 thành nhân tử là

A. (x + 1)(x + 12)

B. (x + 3)(x + 4)

C. (x - 3)(x - 4)

D. (x - 1)(x - 12)

Giải

Xét phương trình x² + 7x + 12 = 0

Phương trình có ∆ = 7² – 4.1.12 = 49 – 48 = 1 > 0 nên có hai nghiệm phân biệt

⇒ x² + 7x + 12 = (x + 3)(x + 4)

Đáp án B

Câu 2: Biểu thức nào sau đây có kết quả phân tích thành nhân tử là (3x – 2)(-x + 7)

A. -3x² + 13x - 14

B. -3x² + 33x - 14

C. -3x² + 23x - 14

D. -3x² + 3x - 14

Giải

Ta có (3x – 2)(-x + 7) = -3x² + 21x + 2x -14 = -3x² + 23x - 14

Đáp án C

Câu 3: Khi phân tích biểu thức 9x² + 12x - 5 thành nhân tử thì một trong hai nhân tử là

A. x - 7

B. x - 2

C. 3x + 2

D. 3x + 5

Giải

Tích ac = -45 = (-5).9 = 5.(-9) = (-3).15 = 3.(-15) = 1.(-45) = (-1).45

Trong các cặp số trên ta chọn cặp số -3 và 15 vì tổng của chúng bằng 12 = b

Đáp án D

Câu 4: Khi phân tích biểu thức x² – 11x + 30 thành nhân tử ta được kết quả là

A. (x – 5)(x – 6)

B. (x + 5)(x + 6)

C. (x – 3)(x – 10)

D. (x – 2)(x – 15)

Giải

Tích ac = 30 = (-5).(-6) = 5.6 = 2.15 = (-2).(-15) = 3.10 = (-3).(-10)

Trong các cặp số trên ta chọn cặp số -5 và -6 vì tổng của chúng bằng -11 = b

Đáp án A

Câu 5: Khi phân tích biểu thức 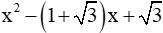 thành nhân tử ta được kết quả là

Giải

Đáp án C

Câu 6: Khi phân tích biểu thức x² – 10x + 21thành (x + a)(x + b) thì tổng của a và b bằng bao nhiêu

A. -9

B. -10

C. -11

D. -12

Giải

Vậy a + b = -7 – 3 = -10

Đáp án B

Câu 7: Khi phân tích biểu thức 4x² – 8x + 3 thành (ax + b)(cx + d) thì tích của b và d bằng bao nhiêu

A. 1

B. 2

C. 3

D. 4

Giải

Vậy tích bd = (-3).(-1) = 3

Đáp án C

Câu 8: Khi phân tích biểu thức 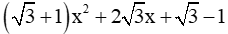 thành nhân tử thì một trong hai nhân tử là

Giải

Xét phương trình 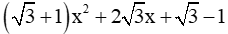 = 0 có:

Do đó phương trình có 2 nghiệm phân biệt: 

Vậy đáp án D