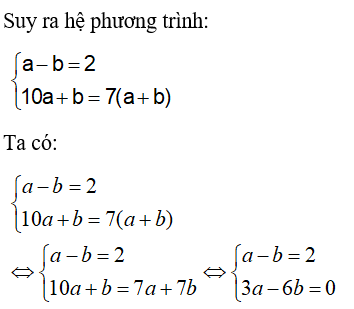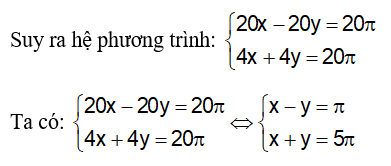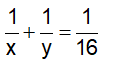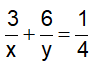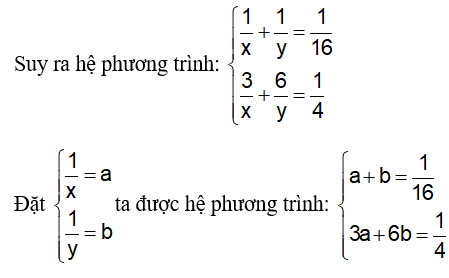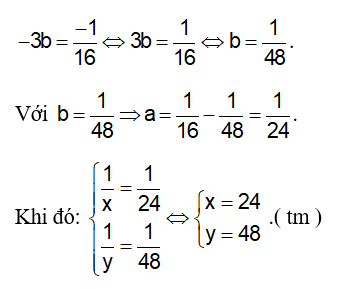Phương pháp giải bài toán bằng cách lập hệ phương trình siêu hay, chi tiết

A. Phương pháp giải

Bước 1: Lập hệ phương trình:

   + Đặt ẩn và tìm điều kiện của ẩn (nếu có).

   + Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

   + Lập hệ phương trình biểu diễn tương quan giữa các đại lượng.

Bước 2: Giải hệ phương trình.

Bước 3: So sánh với điều kiện và kết luận.

B. Ví dụ minh họa

Ví dụ 1: Tìm số có hai chữ số biết chữ số ở hàng chục lớn hơn chữ số hàng đơn vị là 2. Số đó gấp 7 lần tổng hai chữ số của nó.

Hướng dẫn giải:

Gọi số cần tìm là ab với 

Vì chữ số ở hàng chục lớn hơn chữ số hàng đơn vị là 2, nên ta có: a – b = 2

Vì số đó gấp 7 lần tổng hai chữ số của nó, nên ta có: 10a + b = 7(a + b)

Nhân pt (1) với 3 ta được: 3a – 3b = 6 (3)

Lấy pt (3) – pt (2) ta được: 3b = 6 ⇔ b = 2 ( tm )

Với b = 2 ⇒ a = 4 ( tm)

Vậy số cần tìm là: 42.

Ví dụ 2: Hai vật chuyển động đều trên một đường tròn đường kính 20cm, xuất phát cùng một lúc, từ một điểm, nếu chuyển động cùng chiều cứ 20 giây chúng lại gặp nhau, nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau. Tìm vận tốc của mỗi vật.

Hướng dẫn giải:

Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s). ( x , y > 0, giả sử x > y)

Vì nếu chuyển động cùng chiều cứ 20 giây chúng lại gặp nhau nên hiệu quãng đường đi được trong 20 giây của hai vật là chu vi của đường tròn, do đó: 20x – 20y = 20π

Vì nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau nên tổng quãng đường đi được trong 4 giây của hai vật là chu vi của đường tròn, do đó: 4x + 4y = 20 π

Cộng vế theo vế của hai phương trình trên ta được: 2x=6π ⇔ x =3π ( tm)

Với x=3π ⇒ y = 5π-3π = 2π (tm)

Vậy vận tốc của hai vật lần lượt là: 3π(cm/s),2π(cm/s)

Ví dụ 3: Hai người thợ cùng làm chung một công việc trong 16 giờ thi xong. Nếu người thứ nhất làm trong 3 giờ và người thứ hai làm trong 6 giờ thì được 25% khối lượng cộng việc. Hỏi mỗi người làm một mình thì hết bao lâu?

Hướng dẫn giải:

Gọi thời gian để người thứ nhất làm xong công việc đó là x (giờ), ( x > 16)

Gọi thời gian để người thứ hai làm xong công việc đó là y (giờ), ( y > 16)

Vì hai người cùng làm chung công việc trong 16 giờ thi xong, nên ta có: 

Vì người thứ nhất làm trong 3 giờ và người thứ hai làm trong 6 giờ thì được 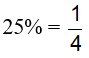 khối lượng cộng việc, nên ta có:

Nhân pt(1) với 3 ta được: 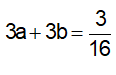 , rồi trừ vế với vế cho pt(2) ta được:

Vậy người thứ nhất làm hết 24 giờ, người thứ hai làm hết 48 giờ.