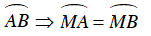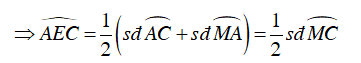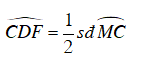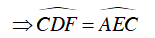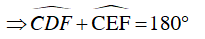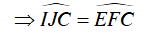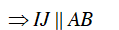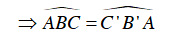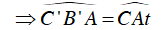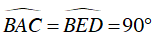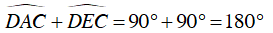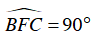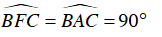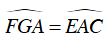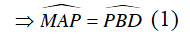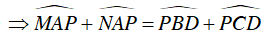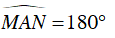Ứng dụng của tứ giác nội tiếp chứng minh song song, vuông góc, thẳng hàng, đồng quy

A. Phương pháp giải

+ Chứng minh 3 điểm M, N, P thẳng hàng

- Ba điểm tạo thành một góc bẹt

- MN//d, MP//d. Theo tiên đề Ơ – clit MN ≡ MP ⇒ M, N, P thẳng hàng

- MN ⊥ d, MP ⊥ d. Qua một điểm nào ngoài một đường thẳng chỉ kẻ được một đường thẳng đi qua điểm đó và vuông góc với đường thẳng đã cho ⇒ MN ≡ MP ⇒ M, N, P thẳng hàng.

+ Chứng minh song song

- Sử dụng các cặp góc so le trong, đồng vị, trong cùng phía

- Các định lý từ vuông góc đến song song, đường trung bình, định lý Thalet,…

+ Chứng minh vuông góc

- Chứng minh góc tạo bởi hai đường thẳng bằng

- Các đường trung trực, đường cao, …

+ Chứng minh đồng quy

- Chứng minh một điểm đồng thời thuộc cả ba đường thẳng đó.

- Chứng minh giao điểm của hai đường thẳng này nằm trên đường thẳng thứ ba.

- Chứng minh giao điểm của hai đường thẳng thứ nhất và thứ hai trùng với giao điểm của hai đường thẳng thứ hai và thứ b.

- Sử dụng tính chất đồng quy của ba đường trung tuyến, đường cao, phân giác, trung trực trong tam giác.

- Sử dụng tính chất của đường chéo của các tứ giác đặc biệt.

Nhận xét

B. Ví dụ minh họa

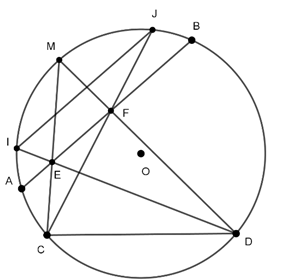
Ví dụ 1 : Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB.

Hướng dẫn giải

M là điểm chính giữa cung nhỏ 

Ta có: 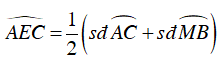 (góc có đỉnh nằm trong đường tròn chắn cung AC và cung MB)

Ta lại có: 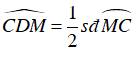 ( góc nội tiếp chắn cung MC) hay 

Mà  (hai góc kề bù)

Suy ra tứ giác DCEF nội tiếp đường tròn

 ( hai góc nội tiếp cùng chắn cung CE)

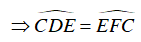
Xét đường tròn (O) ta có: 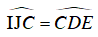 (hai góc nội tiếp cùng chắn cung CI)

Mà hai góc ở vị trí đồng vị

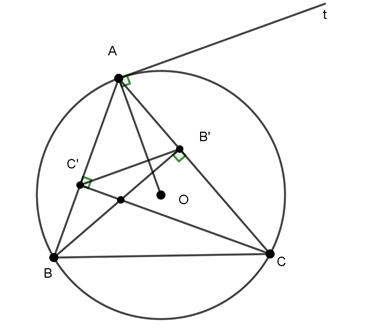
Ví dụ 2 : Cho tam giác ABC, đường cao BB’ và CC’ nội tiếp đường tròn (O). Chứng minh rằng OA vuông góc với B’C’.

Hướng dẫn giải

Ta có: 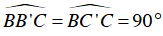 ( Do BB’, CC’ là các đường cao)

⇒ Hai đỉnh liên tiếp C’, B’ cùng nhìn cạnh BC dưới một góc

⇒ Tứ giác BCB’C’ nội tiếp đường tròn đường kính BC.

Do đó: 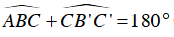 ( hai góc đối nhau)

Mà 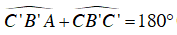 (hai góc kề bù)

Kẻ tia tiếp tuyến At của (O). Khi đó: 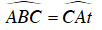 (góc nội tiếp và góc tạo bởi tia tiếp tuyến với dây cung cùng chắn cung AC)

Mà hai góc ở vị trí so le trong

⇒ B’C’//At

Mà At OA

⇒ B’C’ OA.

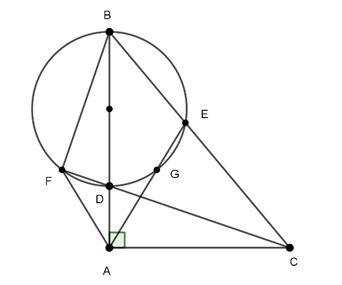
Ví dụ 3 : Cho tam giác ABC vuông ở A. Một điểm D nằm giữa A và B, đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD, AE cắt đường tròn tại F, G. Chứng minh:

a. Hai tam giác ABC và EBD đồng dạng với nhau

b. Tứ giác ADEC và tứ giác AFBC nội tiếp đường tròn

c. AC // FG

d. Các đường thẳng AC, DE và BF đồng quy

Hướng dẫn giải

a. Xét đường tròn đường kính BD

Ta có: 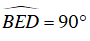 (góc nội tiếp chắn nửa đường tròn)

Xét ΔABC và ΔEBD , ta có:

 chung

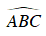
⇒ ΔABC ∼ ΔEBD (g – g)

b. Xét tứ giác ADEC, có: 

Suy ra tứ giác ADEC nội tiếp đường tròn

Ta có: 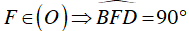 (góc nội tiếp chắn nửa đường tròn) hay 

⇒ 

⇒ A, F cùng nhìn BC dưới một góc

⇒ Tứ giác AFBC nội tiếp đường tròn.

c) Tứ giác BEGF nội tiếp đường tròn

⇒  (1)

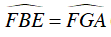
Tứ giác BFDE nội tiếp đường tròn

⇒  (2)

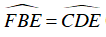
Tứ giác ADEC nội tiếp đương tròn

⇒  ( hai góc nội tiếp cùng chắn cung EC)(3)

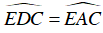
Từ (1), (2) và (3) suy ra: 

Mà hai góc ở vị trí so le trong

⇒ FG//AC.

d) Gọi giao điểm của AC, BF là H

Xét tam giác HBC, có: CF, AB là các đường cao

CF ∩ AB = {D}

⇒ D là trực tâm tam giác HBC

⇒ HD ⊥ BC (1)

Ta lại có

 (góc nội tiếp chắn nửa đường tròn đường kính BD)

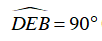
⇒ DE ⊥ BC (2)

Từ (1) và (2) suy ra H, D, E thẳng hàng

Vậy ba đường thẳng AC, DE, BF đồng quy tại H.

Ví dụ 4 : Tứ giác ABCD có 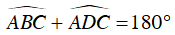 . Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.

Hướng dẫn giải

Tứ giác ABCD có 

ABCD là tứ giác nội tiếp

Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD

⇒ OA = OB = OC = OD = R

Do OA = OC nên ΔOAC cân tại O. Suy ra, O thuộc đường trung trực của AC.

Do OB = OD nên ΔOBD cân tại O. Suy ra, O thuộc đường trung trực của BD

Do OA = OB nên ΔOAB cân tại O. Suy ra, O thuộc đường trung trực của AB.

⇒ O thuộc đường trung trực của AC, BD, AB .

Vậy các đường trung trực của AC, BD, AB cùng đi qua O.

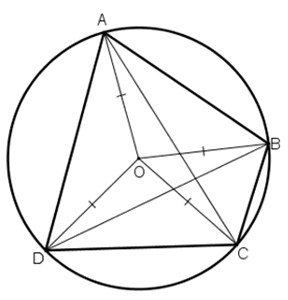
Ví dụ 5 : Cho ba đường tròn cùng đi qua một điểm P. Gọi các giao điểm khác P của hai trong ba đường tròn đó là A, B, C. Từ một điểm D (khác điểm P) trên đường tròn (PBC) kẻ các tia DB, DC cắt các đường tròn (PAB) ,(PAC) lần lượt tại M, N. Chứng minh ba điểm M,A,N thẳng hàng.

Hướng dẫn giải

Gọi I, J, K lần lượt là tâm của ba đường tròn

Ta có: (I) cắt (J) tại A, (I) cắt (K) tại C , (J) cắt (K) tại B

Suy ra: D là điểm nằm trên (K)

DB cắt (I) tại M, DC cắt (J) tại N

Nối MA, NA, PA, PB, PC ta có các tứ giác nội tiếp AMBP, BDCP và APCN

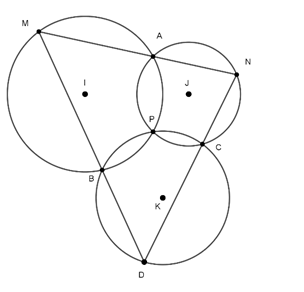
+ Tứ giác APBM nội tiếp trong đường tròn (I) nên ta có:

 (tính chất tứ giác nội tiếp)

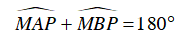
Mà 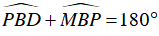 (hai góc kề bù)

+ Tứ giác APCN nội tiếp trong đường tròn (J) nên ta có:

 (tính chất tứ giác nội tiếp)

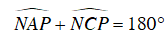
Mà  (hai góc kề bù)

Từ (1) và (2) 

Mặt khác, PBDC là tứ giác nội tiếp (K)

 ( tính chất tứ giác nội tiếp)

 hay 

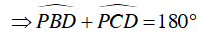
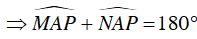
Vậy A, M, N thẳng hàng.