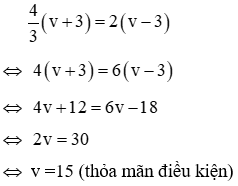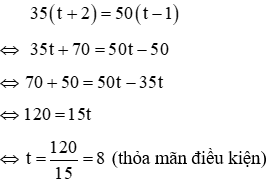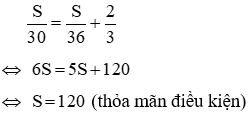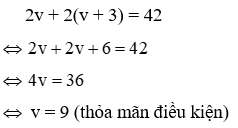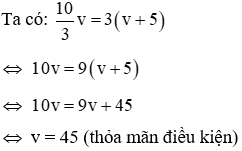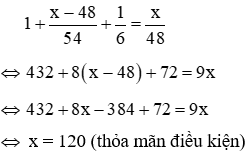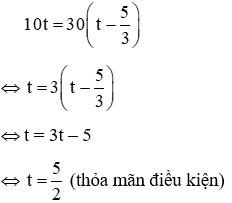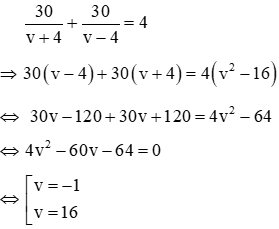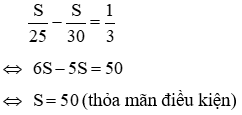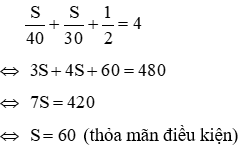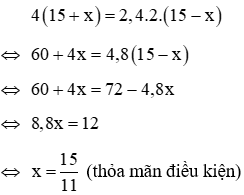Giải bài toán bằng cách lập phương trình – Dạng toán chuyển động

A. Phương pháp giải

B1: Lập phương trình

- Chọn ẩn số và đặt điều kiện cho ẩn

- Biểu diễn các dữ kiện chưa biết qua ẩn số

- Lập phương trình biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Một số lưu ý:

- quãng đường = vận tốc  × thời gian

- vận tốc xuôi dòng = vận tốc khi nước yên lặng + vận tốc dòng nước

- vận tốc ngược dòng = vận tốc khi nước yên lặng - vận tốc dòng nước

Ví dụ 1: Một ca nô đi xuôi dòng từ A đến B hết 1 giờ 20 phút và ngược dòng từ B về A hết 2 giờ. Tính vận tốc riêng của ca nô, biết vận tốc dòng nước là 3km/h

Giải

Đổi 1 giờ 20 phút = 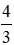 giờ

Gọi vận tốc riêng của ca nô là v ( v > 3)

Vận tốc của ca nô khi xuôi dòng là: v + 3 (km/h)

 quãng đường AB là: 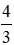(v + 3) km   (1)

Vận tốc của ca nô khi ngược dòng là: v - 3 (km/h)

 quãng đường AB là: 2(v - 3) km   (2)

Từ (1) và (2) ta có phương trình:

Vậy vận tốc riêng của ca nô là 15(km/h)

Ví dụ 2: Một ô tô đi từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc 35km/h thì đến chậm mất 2 giờ. Nếu xe chạy với vận tốc 50km/h thì đến sớm hơn 1 giờ. Tính quãng đường AB và thời gian dự định lúc đầu

Giải

Gọi t là thời gian dự định lúc đầu ( t đơn vị là giờ, t > 1)

Nếu xe chạy với vận tốc 35km/h thì thời gian đi từ A đến B là: t + 2 (giờ)

⇒ quãng đường AB là: 35.(t + 2) km  (1)

Nếu xe chạy với vận tốc 50km/h thì thời gian đi tử A đến B là: t - 1 (giờ)

⇒ quãng đường AB là: 50.(t - 1) km (2)

Từ (1) và (2) ta có phương trình:

Vậy thời gian dự định ban đầu là 8(giờ) và quãng đường AB dài 35.(t + 2) = 35.10 = 350 (km)

B. Bài tập

Câu 1: Hai xe máy khởi hành lúc 7 giờ sáng từ A đến B. Xe thứ nhất chạy với vận tốc 30km/h, xe thứ hai chạy với vận tốc lớn hơn xe thứ nhất 6km/h. Trên đường đi xe thứ hai dừng lại nghỉ 40 phút rồi lại tiếp tục chạy với vận tốc cũ. Tính quãng đường AB biết hai xe về đến B cùng một lúc

A. 100km

B. 110km

C. 120km

D. 130km

Giải

Đổi 40 phút = 2/3 giờ

Gọi S là quãng đường AB (S > 0, S đơn vị đo là km)

Thời gian đi từ A đến B của xe thứ nhất là: 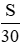 (giờ)

Vận tốc của xe thứ hai là 36km/h

Thời gian đi từ A đến B của xe thứ hai là: 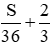 (giờ)

Vì hai xe về B cùng một lúc nên thời gian đi từ A đến B của hai xe là như nhau.  Do đó ta có phương trình :

Vậy quãng đường AB dài 120 km

Đáp án là C

Câu 2: Hai người đi xe đạp cùng lúc, ngược chiều nhau từ hai địa điểm A và B cách nhau 42km và gặp nhau sau 2 giờ. Tính vận tốc của mỗi người biết rằng người đi từ A mỗi giờ đi nhanh hơn người đi từ B là 3km

A. 10km/h và 13km/h

B. 9km/h và 12km/h

C. 12km/h và 15km/h

D. 13km/h và 16km/h

Giải

Gọi vận tốc của người đi từ A là v (v > 0, v đơn vị là km/h)

⇒ vận tốc của người đi từ B là: v + 3 (km/h)

Quãng đường người xuất phát từ A đi được là: 2v (km)

Quãng đường người xuất phát từ B đi được là: 2(v + 3) (km)

Tổng quãng đường mà hai người đi được là quãng đường AB nên ta có phương trình:

Vậy vận tốc của người đi từ A là 9km/h, của người đi từ B là 12km/h

Đáp án là B

Câu 3: Một người đi xe máy từ A đến B dự định mất 3 giờ 20 phút. Nếu người ấy tăng vận tốc thêm 5km/h thì sẽ đến B sớm hơn 20 phút. Tính quãng đường AB và vận tốc dự định của người đó

A. 30km/h và 120km

B. 35km/h và 120km

C. 45km/h và 150km

D. 40km/h và 150km

Giải

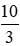
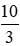
Gọi vận tốc dự định của người đó là vkm /h (v > 0). Vì thời gian để người đó đi hết quãng đường AB là  giờ nên quãng đường AB là: v (km)

Vận tốc của người đó sau khi tăng thêm 5km/h là: v + 5(km /h). Vì thời gian để người đó đi hết quãng đường AB là 3 giờ nên quãng đường AB là: 3(v + 5) km

Vậy vận tốc dự định của người đó là 45km/h và do đó quãng đường AB là:

3 (v + 5) = 3(45 + 5) = 150 km

Đáp án là C

Câu 4: Một người đi ô tô từ A đến B với vận tốc dự định là 48km/h. Nhưng khi đi được 1 giờ với vận tốc ấy người đó nghỉ 10 phút và tiếp tục đi đến B kịp thời gian đã định người đó phải tăng vận tốc thêm 6km/h. Tính quãng đường AB

A.  110km

B. 120km

C. 130km

D. 140km

Giải

Đổi 10 phút = 1/6 giờ

Gọi chiều dài quãng đường AB là xkm (x > 48)

Thời gian mà người đó dự định đi hết quãng đường AB là 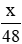 (giờ)

Trong 1 giờ đầu người đó đi được 48km

⇒  quãng đường còn lại là: x – 48 (km)

Sau khi tăng vận tốc thêm 6km/h thì vận tốc mới của ô tô là 54km/h

⇒  thời gian để người đó đi hết x – 48 (km) đường còn lại là: 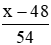 (giờ)

Vì tổng thời gian đi và nghỉ của ô tô bằng thời gian dự định ban đầu nên ta có phương trình

Vậy quãng đường AB dài 120km

Đáp án đúng là B

Câu 5: Lúc 7 giờ sáng một người đi xe đạp xuất phát từ A với vận tốc 10km/h. Sau đó lúc 8 giờ 40 phút, một người khác đi xe máy từ A đuổi theo với vận tốc 30km/h. Hỏi hai người gặp nhau lúc mấy giờ?

A. 9 giờ 10 phút

B. 9 giờ 20 phút

C. 9 giờ 30 phút

D. 9 giờ 40 phút

Giải

Người đi xe đạp khởi hành lúc 7 giờ, người đi xe máy khởi hành lúc 8 giờ 40 phút. Như vậy người đi xe máy khởi hành sau người đi xe đạp 1 giờ 40 phút hay 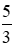 giờ

Gọi t là thời gian người đi xe đạp đi từ khi khởi hành đến lúc hai người gặp nhau (t > 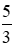, t đơn vị là giờ)

Thời gian người đi xe máy đi từ khi khởi hành đến lúc hai người gặp nhau là: t - 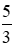 (giờ)

⇒  quãng đường người đi xe máy đi được là: 30( t - 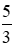) (km)

Vì hai người cùng khởi hành ở A nên đến khi gặp nhau thì đi được quãng đường như nhau. Do đó ta có phương trình:

Suy ra hai xe gặp nhau sau khi người đi xe đạp đi được 2,5 giờ, tức là lúc 9 giờ 30 phút

Đáp án là C

Câu 6: Một ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 4 giờ. Tính vận tốc của ca nô khi nước yên lặng, biết rằng quãng sông AB dài 30km và vận tốc dòng nước là 4km/h

A. 13km/h

B. 14km/h

C. 15km/h

D. 16km/h

Giải

Gọi vận tốc của ca nô khi nước yên lặng là v km/h (v > 4)

Vận tốc của ca nô khi xuôi dòng là: v + 4 (km/h)

⇒   thời gian ca nô đi xuôi dòng từ A đến B là: 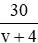 (giờ)

Vận tốc của ca nô khi ngược dòng là: v - 4 (km/h)

 thời gian ca nô đi ngược dòng từ B đến A là: 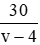 (giờ)

Vì tổng thời gian đi và về là 4 giờ nên ta có phương trình

Với v = -1 không thỏa mãn nên loại

Với v = 16 thỏa mãn điều kiện nên nhận

Vậy vận tốc của ca nô khi nước yên lặng là 16km/h

Đáp án là D

Câu 7: Một người đi xe máy từ A đến B vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h nên thời gian về ít hơn thời gian đi là 20 phút. Tính quãng đường AB

A. 20km

B. 30km

C. 40km

D. 50km

Giải

Đổi 20 phút = 1/3 giờ

Gọi S là quãng đường AB (S > 0, S đơn vị đo là km)

Vì thời gian về ít hơn thời gian đi là 1/3 giờ nên ta có phương trình

Vậy quãng đường AB dài 50 km

Đáp án là D

Câu 8: Lúc 6 giờ sáng một ô tô xuất phát từ A đến B với vận tốc 40km/h. Khi đến B người đó làm nhiệm vụ giao nhận hàng trong 30 phút rồi cho xe quay về A với vận tốc 30km/h. Tính quãng đường AB biết ô tô về đến A lúc 10 giờ sáng cùng ngày

A. 60km

B. 70km

C. 80km

D. 90km

Giải

Đổi 30 phút = 1/2 giờ

Gọi S là quãng đường AB (S > 0, S đơn vị đo là km)

Vì xe quay về A lúc 10 giờ cùng ngày nên tổng thời gian đi, về và giao hàng là 4 giờ. Từ đó ta có phương trình

Vậy quãng đường AB dài 60 km

Đáp án là A

Câu 9: Quãng đường một ca nô chạy xuôi dòng trong 4 giờ bằng 2,4 lần quãng đường ca nô đi ngược dòng trong 2 giờ. Tính vận tốc của ca nô khi xuôi dòng, biết rằng vận tốc của ca nô khi nước yên lặng là 15km/h.

Giải

Gọi vận tốc của dòng nước là xkm/h (x  > 0)

Vận tốc của ca nô khi xuôi dòng là: x + 15 (km/h)

⇒   quãng đường ca nô đi xuôi dòng trong 4 giờ là: 4(x + 15) km

Vận tốc của ca nô khi ngược dòng là: 15 - x (km/h)

⇒   quãng đường ca nô đi ngược dòng trong 2 giờ là: 2(15 – x) km

Vì quãng đường ca nô chạy xuôi dòng trong 4 giờ bằng 2,4 lần quãng đường ca nô đi ngược dòng trong 2 giờ nên ta có phương trình:

Vậy vận tốc của ca nô khi xuôi dòng là: 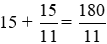 (km/h)

Đáp án là A