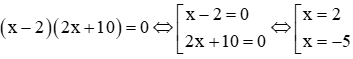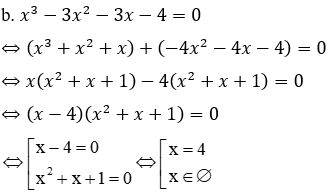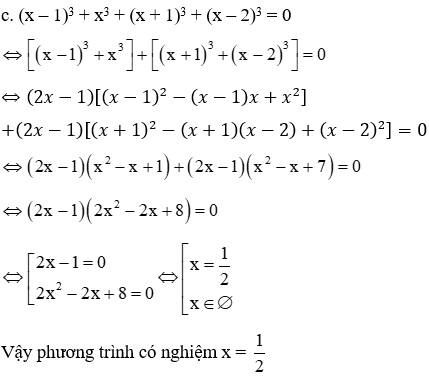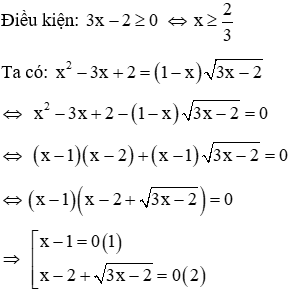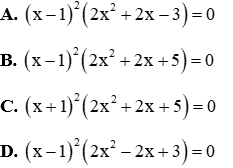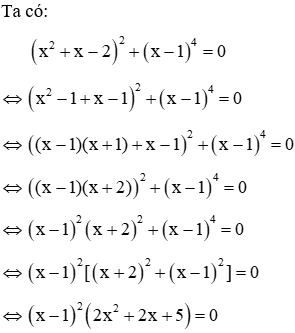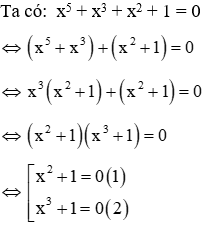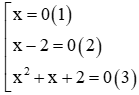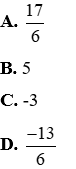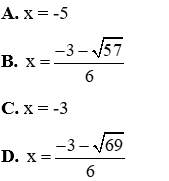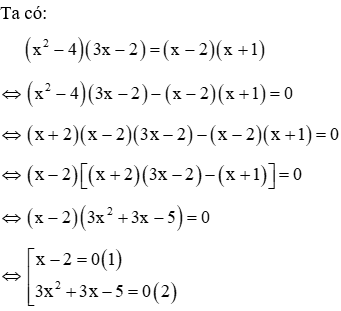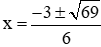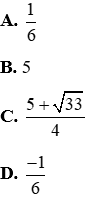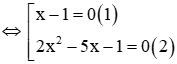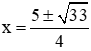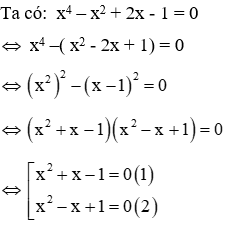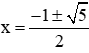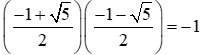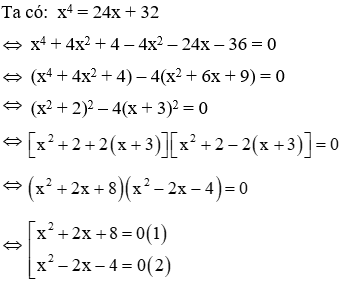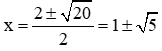Phương pháp giải phương trình đưa về dạng tích cực hay

A. Phương pháp giải

Để giải phương trình đưa về dạng tích ta làm như sau:

B1: Chuyển vế, phân tích vế trái thành nhân tử, vế phải bằng không

B2: Xét từng nhân tử bằng không để tìm nghiệm

Ví dụ: Giải các phương trình sau

a. (x – 2)( 2x + 10) = 0

b. x³ - 3x² - 3x - 4 = 0

c. (x – 1)³ + x³ + (x + 1)³ + (x – 2)³ = 0

Giải

a. 

Vậy phương trình có 2 nghiệm: x = 2, x = -5

Vậy phương trình có nghiệm x = 4

B. Bài tập

Câu 1: Số nghiệm của phương trình 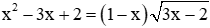 là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình (1) có nghiệm x = 1 (thỏa mãn điều kiện)

Thử lại ta thấy x = 1 là nghiệm của phương trình (2) và thỏa mãn điều kiện nên nhận

x = 6 không là nghiệm của phương trình (2) nên loại

Vậy phương trình có 1 nghiệm x = 1

Đáp án là B

Câu 2: Phương trình (x² + x - 2)² + (x - 1)⁴ = 0  sau khi đưa về phương trình tích là phương trình nào sau đây

Giải

Đáp án đúng là B

Câu 3: Số nghiệm của phương trình  x⁵ + x³ + x² + 1 = 0 là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình (1) vô nghiệm

Phương trình (2) ⇔ x³ = -1 ⇔ x = -1

Vậy phương trình có 1 nghiệm

Đáp án là B

Câu 4: Số nghiệm của phương trình  x(x – 2)(x² + x + 2) = 0 là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình  x(x – 2)(x² + x + 2) = 0 ⇔  

Phương trình (1) có nghiệm x = 0

Phương trình (2) có nghiệm x = 2

Phương trình (3) có ∆ = 1² – 4.1.2 = -7 < 0 nên phương trình vô nghiệm

Vậy phương trình đã cho có 2 nghiệm

Đáp án là C

Câu 5: Tổng các nghiệm của phương trình  (x² + 2x - 5)² = (x² - x + 5)²  là

Giải

Phương trình  (x² + 2x - 5)² = (x² - x + 5)²

⇔  (x² + 2x - 5)² - (x² - x + 5)² = 0

⇔ [(x² + 2x - 5) - (x² - x + 5)][(x² + 2x - 5) + (x² - x + 5)] = 0

⇔ (3x – 10)(2x² + x) = 0

Đáp án là A

Câu 6: Nghiệm nhỏ nhất của phương trình (x² - 4)(3x - 2)=(x - 2)(x + 1)  là

Giải

Phương trình (1) có nghiệm x = 2

Phương trình (2) có ∆ = 3² – 4.3.(-5) = 69 > 0 nên phương trình có hai nghiệm phân biệt: 

Vậy nghiệm nhỏ nhất của phương trình là: 

Đáp án đúng là D

Câu 7: Nghiệm lớn nhất của phương trình 2x³ – 7x² + 4x + 1 = 0

Giải

Phương trình  2x³ – 7x² + 4x + 1 = 0

⇔ (2x³ – 5x² – x) – (2x² – 5x – 1) = 0

⇔ x(2x² – 5x – 1) – (2x² – 5x – 1) = 0

⇔ (2x² – 5x – 1)(x – 1)  = 0

Phương trình (1) có nghiệm x = 1

Phương trình (2) có ∆ = (-5)² – 4.2.(-1) = 25 + 8 = 33 > 0 nên phương trình có 2 nghiệm phân biệt: 

Vậy nghiệm lớn nhất của phương trình là: 

Đáp án là C

Câu 8: Tích các nghiệm của phương trình  x⁴ – x² + 2x - 1 = 0

A. -1               

B. 2

C. -2              

D. 3

Giải

Phương trình (1) có ∆ = 1² – 4.1.(-1) = 5 > 0 nên có 2 nghiệm phân biệt: 

Phương trình (2) có ∆ = (-1)² – 4.1.1 = -3 < 0 nên vô nghiệm

Vậy phương trình có 2 nghiệm: 

Suy ra tích các nghiệm của phương trình là: 

Đáp án là A

Câu 9: Số nghiệm của phương trình  x⁴ = 24x + 32 là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình (1) có ∆ = 2² – 4.1.8 = -28 < 0 nên phương trình vô nghiệm

Phương trình (2) có ∆ = (-2)² – 4.1.(-4)  = 20 > 0 nên phương trình có hai nghiệm phân biệt:

Vậy phương trình đã cho có 2 nghiệm

Đáp án là C