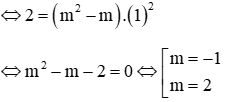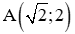Cách xác định hệ số a của hàm số y = ax² hay, chi tiết

A. Phương pháp giải

Bài toán 1: Cho hàm số y = ax² . Tìm a để đồ thị hàm số đi qua M(x₀;y₀)

Cách giải: Thay tọa độ của điểm M vào công thức của hàm số được phương trình y₀ = ax₀² (1). Giải phương trình (1) tìm a

Bài toán 2: Cho hàm số y = ax² (trong đó a = f(m)). Tìm m để hàm số đã cho là hàm số bậc hai

Cách giải: Để hàm số y = ax² là hàm số bậc hai thì hệ số a ≠ 0 hay f(m) ≠ 0. Giải điều kiện này ta tìm được m

Bài toán 3: Cho hàm số y = ax² (trong đó a = f(m)). Tìm m để hàm số đã cho đồng biến hoặc nghịch biến

Cách giải: Ta sử dụng kết quả

+ Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0

+ Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0

Ví dụ 1: Tìm m để hàm số y = (m – 4)x² đồng biến với mọi x > 0

Giải:

Hàm số y = (m – 4)x² đồng biến với mọi x > 0 khi hệ số a = m – 4 > 0 hay m > 4

Vậy với m > 4 thì hàm số đồng biến với mọi x > 0

Ví dụ 2: Cho hàm số y = (m² – m)x². Tìm m để đồ thị hàm số đi qua điểm A(1;2)

Giải:

Đồ thị hàm số đi qua điểm A(1;2)   

Vậy với m = -1 hoặc m = 2 thì đồ thị hàm số đi qua điểm A(1;2)

Ví dụ 3: Tìm m để hàm số y = (m + 2)x² là hàm số bậc hai

Giải:

Để hàm số đã cho là hàm số bậc hai thì hệ số a = m + 2 ≠ 0 ⇔ m ≠ -2

Vậy với m ≠ -2 thì hàm số đã cho là hàm số bậc hai

Cho hàm số y = ax². Tìm a để đồ thị hàm số đi qua điểm A(-2;8)

Giải:

Đồ thị hàm số đi qua điểm A(-2;8) ⇔ 8 = a(-2)² ⇔ 8 = 4a ⇔ a = 2

Vậy với a = 2 thì  đồ thị hàm số đi qua điểm A(-2;8)

B. Bài tập

Câu 1: Tìm m để hàm số y = (m² – 2)x²  là hàm số bậc hai

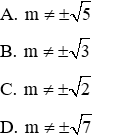
Giải

Để hàm số đã cho là hàm số bậc hai thì hệ số a = m² - 2 ≠ 0 ⇔ m² ≠ 2 ⇔ 

Vậy với 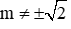 thì hàm số đã cho là hàm số bậc hai.

Đáp án C

Câu 2: Tìm m để hàm số y = (m – 4)x² nghịch biến với mọi x > 0

A. m = 5

B. m < 4

C. m < 10

D. m = ±9

Giải

Hàm số y = (m – 4)x² nghịch biến với mọi x > 0 khi hệ số a = m – 4 < 0

hay m < 4

Vậy với m < 4 thì hàm số nghịch biến với mọi x > 0

Đáp án B

Câu 3: Tìm m để hàm số y = (m² – m)x² đồng biến với mọi x > 0

A. m < 0 hoặc m > 1

B. m < -1 hoặc m > 1

C. m < -2 hoặc m > 1

D. m < -6 hoặc m > 10

Giải

Hàm số y = (m² – m)x² đồng biến với mọi x > 0 khi hệ số a = m² – m > 0

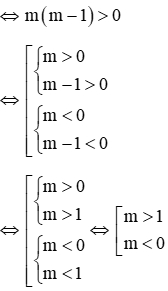
Vậy với m > 1 hoặc m < 0 thì hàm số đồng biến với mọi x > 0

Đáp án A

Câu 4: Tìm a để hàm số y = (2a² – 6a)x² là hàm số bậc hai

A. a ≠ -7 và a ≠ -1

B. a ≠ 0 và a ≠ 3

C. a ≠ 5 và a ≠ -1

D. a ≠ 4 và a ≠ 1

Giải

Để hàm số đã cho là hàm số bậc hai thì 2a² – 6a ≠ 0

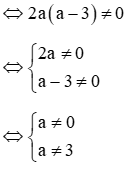
Vậy với a ≠ 0 và a ≠ 3 thì hàm số đã cho là hàm số bậc hai

Câu 5: Tìm m để hàm số y = (m² – m)x² nghịch biến với mọi x > 0

A. -1 < m < 1

B. -2 < m < 1

C. 0 < m < 1

D. -3 < m < 4

Giải

Hàm số y = (m² – m)x² nghịch biến với mọi x > 0 khi hệ số a = m² – m < 0

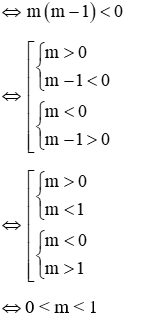
Vậy với 0 < m < 1 thì hàm số nghịch biến với mọi x > 0

Đáp án C

Câu 6: Tìm m để hàm số y = (m² – 3m + 2)x² là hàm số bậc hai

A. m ≠ -2 và m ≠ -1

B. m ≠ 2 và m ≠ -1

C. m ≠ 3 và m ≠ 1

D. m ≠ 2 và m ≠ 1

Giải

Để hàm số đã cho là hàm số bậc hai thì hệ số a = m² – 3m + 2 ≠ 0

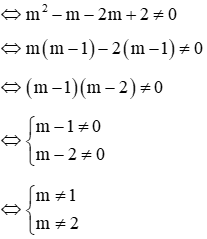
Vậy với m ≠ 2 và m≠ 1 thì hàm số đã cho là hàm số bậc hai

Đáp án D

Câu 7: Cho hàm số y = (k² – 2k + 3)x². Tìm k để đồ thị hàm số đi qua điểm A(1;6)

A. k = 1, k = 2

B. k = -1, k = 3

C. k = 2, k = 5

D. k = 3, k = -4

Giải

Đồ thị hàm số đi qua điểm A(1;6)                                    

Vậy với k = -1 hoặc k = 3 thì đồ thị hàm số đi qua điểm A(1;6)

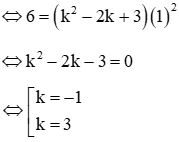
Đáp án B

Câu 8: Cho hàm số y = (m + 1)x². Tìm m để đồ thị hàm số đi qua điểm A(-4;32)

A. m = 1

B. m = 2

C. m = 3

D. m = 4

Giải

Đồ thị hàm số đi qua điểm A(-4;32)                                     

Vậy với m = 1 thì đồ thị hàm số đi qua điểm A(-4;32) ⇔ 32 = (m + 1)(-4)²

⇔ 32 = (m + 1)16 ⇔ m + 1 = 2 ⇔ m = 1

Đáp án A

Câu 9: Cho hàm số y = ax². Tìm a để đồ thị hàm số đi qua điểm 

A. a = -1

B. a = 22

C. a = 3

D. a = 1

Giải

Đồ thị hàm số đi qua điểm 

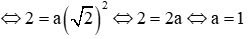
Vậy với a = 1 thì đồ thị hàm số đi qua điểm 

Đáp án D