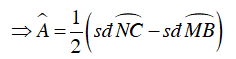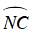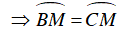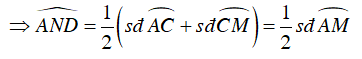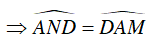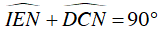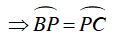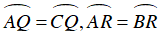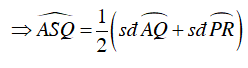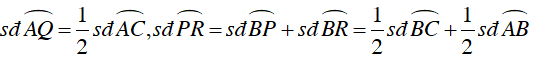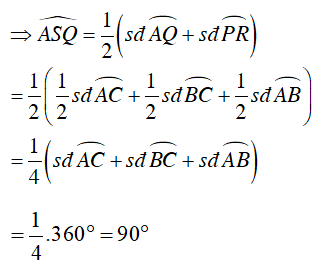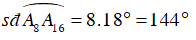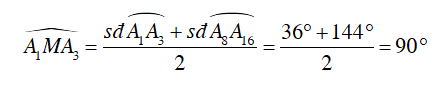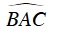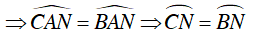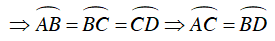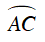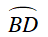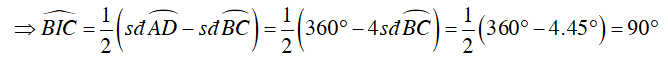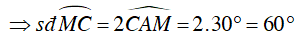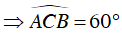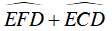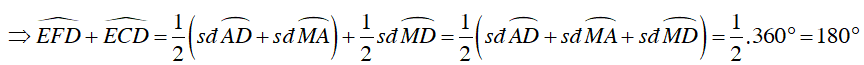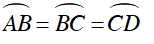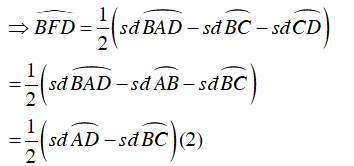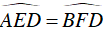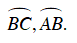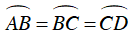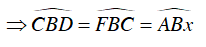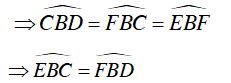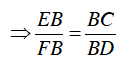Cách chứng minh hai đường thẳng vuông góc cực hay, chi tiết

A. Phương pháp giải

+ Ta thường sử dụng các kiến thức về số đo của góc có đỉnh bên trong và bên ngoài đường tròn, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau.

- Các góc nội tiếp, góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung

- Tính số đo góc cụ thể

+ Chứng minh hai đường thẳng vuông góc bằng cách:

- Chứng minh góc tạo bởi hai đường thẳng bằng 90^o

- Từ song song đến vuông góc

- Đường trung trực, đường cao,…

B. Ví dụ minh họa

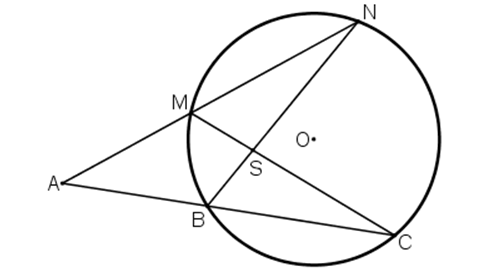
Ví dụ 1 : Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.

Chứng minh  .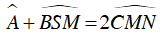

Hướng dẫn giải

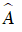
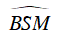
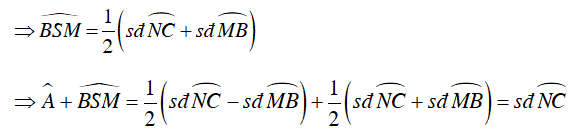
Góc  là góc có đỉnh ở bên ngoài đường tròn (O) chắn hai cung NC và BM

Góc  là góc có đỉnh ở bên trong đường tròn (O) chắn hai cung NC và BM

 (1)

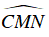
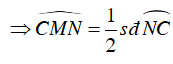
Ta có  là góc nội tiếp chắn cung 

 (2)

Từ (1) và (2) suy ra  .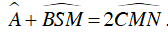

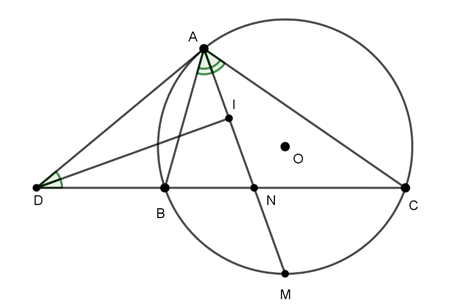
Ví dụ 2 : A, B, C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D.Tia phân giác của góc (BAC) cắt đường tròn ở M, tia phân giác của góc D cắt AM ở I. Chứng minh DI ⊥ AM.

Hướng dẫn giải

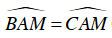
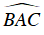
Ta có  (AM là tia phân giác của  )

Gọi N là giao điểm của BD và AM

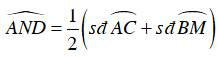
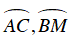
Ta có:  (góc có đỉnh năm bên trong đường tròn chắn hai cung  )

Ta lại có: 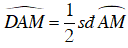 (góc tạo bởi tia tiếp tuyến và dây cung chắn cung AM)

Suy ra tam giác AND cân tại D

Tam giác AND cân tại D có DI là tia phân giác nên DI cũng là đường cao

Suy ra: DI ⊥ AM hay DI ⊥ AM

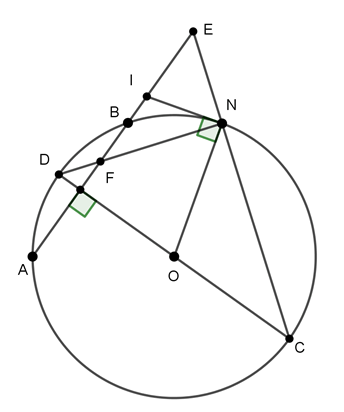
Ví dụ 3 : Cho đường tròn tâm O và dây cung AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung BC nhỏ, lấy điểm N. Các đường thẳng CN, DN cắt AB lần lượt tại E,F. Tiếp tuyến tại N của (O) cắt AB tại I. Chứng minh

a) Tam giác IEN, IFN cân

b) 

Hướng dẫn giải

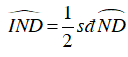
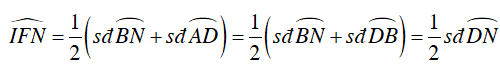
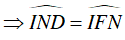
a) Ta có:  ( góc tạo bởi tia tiếp tuyến với dây cung chắn cung ND)

 (góc có đỉnh nằm ở bên trong đường tròn)

 ⇒ ΔIFN cân tại I

+ Gọi H là giao của CD và AB

Xét tam giác vuông EHC, có: 

Ta lại có: 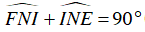 (hai góc phụ nhau)

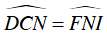
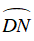
Mà  (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung  )

Suy ra 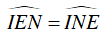 ⇒ ΔIEN cân tại I.

b) Từ a ta có: IN = IF = IE

AE + AF = AF + IE + IF + AF = AF + IF + IF + AF = 2AI

⇒ .

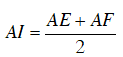
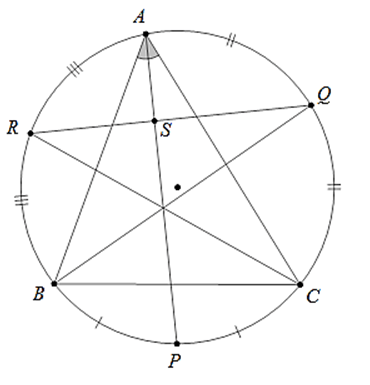
Ví dụ 4 : Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi P, Q, R lần lượt là giao điểm của các tia phân giác trong góc A, B, C với đường tròn. Chứng minh: AP ⊥ QR

Hướng dẫn giải

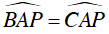
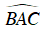
Ta có:  ( vì AP là tia phân giác của góc  )

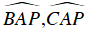
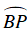
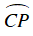
Mà  lần lượt là các góc nội tiếp chắn cung  và  .

Tương tự 

Gọi S là giao điểm của AP và QR. Khi đó:

 là góc có đỉnh nằm trong đường tròn chắn cung  và  .

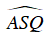
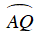
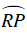
Vì 

⇒ AP ⊥ QR

Vậy ⊥ QR

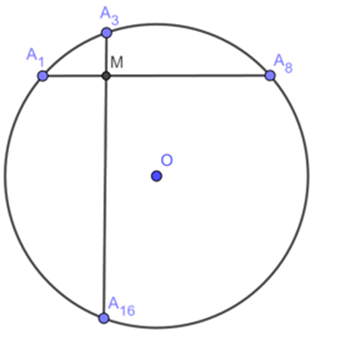
Ví dụ 5 : Các điểm A₁,A₂,A₃,….A₁₉,A₂₀ được sắp xếp theo thứ tự đó trên đường tròn (O) và chia đường tròn thành 20 cung bằng nhau.Chứng minh rằng dây A₁A₈ vuông góc với dây A₃A₁₆

Hướng dẫn giải

Gọi giao điểm của A₁A₈ và A₃A₁₆ là M.

Vì đường tròn được chia thành 20 cung bằng nhau nên số đo của mỗi cung là :

360^o : 20 = 18^o

Ta có: 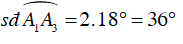 và 

Vì 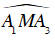 là góc có đỉnh bên trong đường tròn (O) nên:

Suy ra A₁A₈ ⊥ A₃A₁₆

Vậy dây A₁A₈ vuông góc với dây A₃A₁₆.

C. Bài tập trắc nghiệm

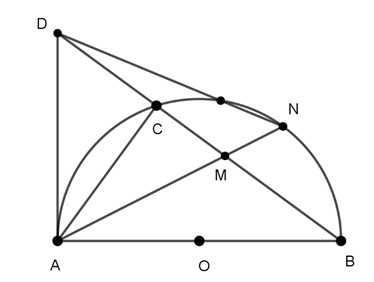
Câu 1 : Cho nửa đường tròn tâm O đường kính AB, C là điểm tùy ý trên nửa đường tròn.Tiếp tuyến của (O) tại A cắt tia BC tại D.Tia phân giác của góc BAC cắt dây BC tại M và cung BC tại N. ΔDAM là tam giác gì?

A.Tam giác vuông

B.Tam giác vuông cân

C.Tam giác cân

D.Tam giác đều

Hướng dẫn giải

Đáp án C

Vì AM là phân giác của 

Ta có: 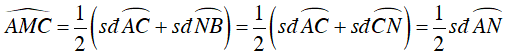 ( góc có đỉnh nằm trong đường tròn chắn cung AC, BN)

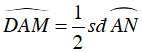
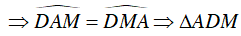
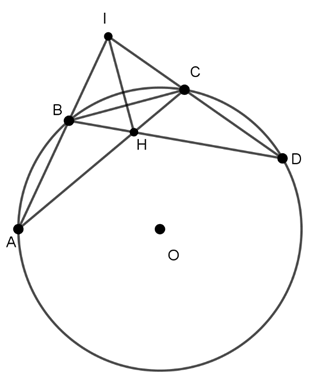
Ta lại có:  ( góc tạo bởi tia tiếp tuyến và dây cung chắn cung AN)

 cân tại D.

Câu 2 : Trên đường tròn (O) lấy ba cung liên tiếp AB = BC = CD sao cho số đo của chúng đều bằng 45^o .Gọi I là giao điểm của hai tia AB và DC, H là giao điểm của hai dây AC và BD. Khẳng định nào sau đây đúng?

A.ΔIBC là tam giác vuông

B.ΔIBC là tam giác cân

C. ΔIBC là tam giác vuông cân

D. A,B,C đều đúng

Hướng dẫn giải

Đáp án C

Ta có AB = BC = CD

 là góc nội tiếp chắn 

 là góc nội tiếp chắn 

 (hai góc nội tiếp cùng chắn hai cung bằng nhau)

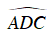
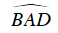
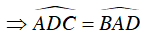
⇒ ΔIAD cân tại I ⇒ IA = ID

Mà AB = CD

⇒ IB = IC ⇒ ΔIBC cân tại I

Ta lại có 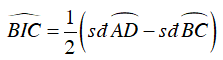 ( góc có đỉnh nằm ngoài đường tròn chắn cung AD, BC)

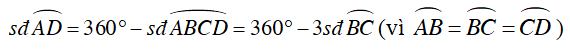
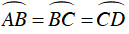
Mặt khác  (vì  )

⇒ ΔIBC vuông cân.

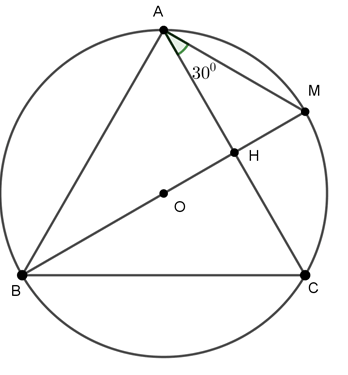
Câu 3 : Cho tam giác đều ABC nội tiếp trog đường tròn tâm O; M là một điểm trên cung nhỏ AC (M khác A và C) sao cho 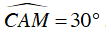 .Góc giữa hai đường thẳng AC và BM là:

A.45

B.60

C.65

D.90

Hướng dẫn giải

Đáp án D

Gọi giao điểm của BM và AC là H

Ta có: 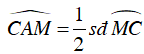 ( góc nội tiếp chắn cung MC)

Ta lại có: ΔABC đều

 ( góc nội tiếp chắn cung AB)

 .

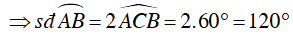
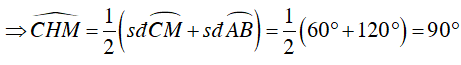
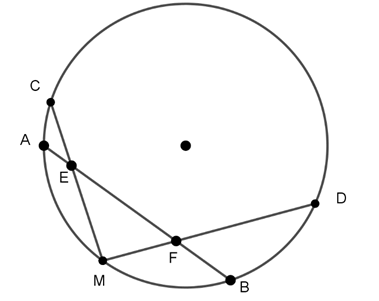
Câu 4 : Cho đường tròn tâm O bán kính R và dây AB bất kỳ. Gọi M là điểm chính giữa của cung nhỏ AB. E và F là hai điểm bất kỳ trên dây AB. Gọi C và D tương ứng là giao điểm của ME, MF của đường tròn (O). Tính tổng 

A. 360^o

B. 180^o

C. 270^o

D. 90^o

Hướng dẫn giải

Đáp án B

Ta có M là điểm chính giữa cung nhỏ AB

 (1)

 (góc có đỉnh nằm bên trong đường tròn chắn hai cung  và  )

 (góc nội tiếp chắn cung MD)

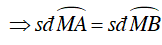
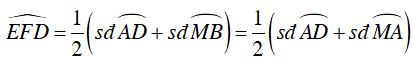
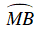
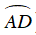
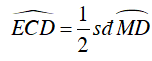
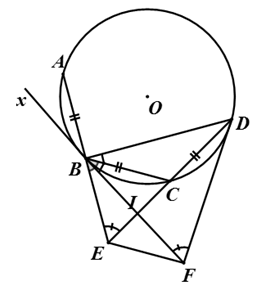
Câu 5 : Trên đường tròn (O; R) đặt liên tiếp các dây cung: AB = BC = CD < R. AB cắt CD tại E. Tiếp tuyến tại B và D với đường tròn (O) cắt nhau tại F. Biểu thức nào dưới đây đúng:

Hướng dẫn giải

Đáp án A

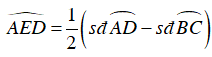
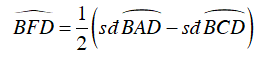
Ta có:  (góc có đỉnh năm bên ngoài đường tròn chắn hai cung AD và BC) (1)

 (góc có đỉnh nằm ngoài đường tròn chắn cung AD )

Mà AB = CB = CD ⇒ 

Từ (1) và (2)⇒ 

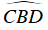
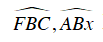
Ta có:  là góc nội tiếp chắn cung CD

 là góc tạo bởi tia tiếp tuyến và dây cung lần lượt chắn các cung 

Mà 

Mà  (hai góc đối đỉnh)

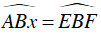
Xét ΔEBC và ΔFBD , ta có:

⇒ ΔEBC ∼ ΔFBD (g - g)