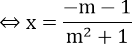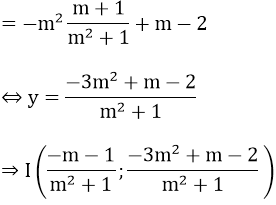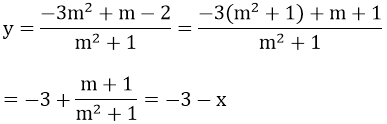Cách xác định đường thẳng cực hay, có đáp án

Phương pháp giải

    Gọi hàm số cần tìm là: y = ax + b (a ≠ 0), ta phải tìm a và b

    + Với điều kiện của bài toán, ta xác định được các hệ thức liên hệ giữa a và b.

    + Giải phương trình để tìm a, b.

Ví dụ minh họa

Ví dụ 1:: Cho hàm số bậc nhất: y = -2x + b. Xác định b nếu:

    a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2.

    b) Đồ thị hàm số đi qua điểm A (-1; 2).

Hướng dẫn:

    a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2 nên b = -2.

    Vậy hàm số cần tìm là y = -2x – 2.

    b) Đồ thị hàm số y = -2x + b đi qua điểm A(-1; 2) nên:

    2 = -2.(-1) + b ⇔ 2 = 2 + b ⇔ b = 0.

    Vậy hàm số cần tìm là y = -2x.

Ví dụ 2: Cho hàm số y = (m - 2)x + m + 2. Xác định m, biết:

    a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -2.

    b) Đồ thị hàm số đi qua gốc tọa độ.

Hướng dẫn:

    a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 2 nên điểm A (-2; 0) thuộc đồ thị hàm số.

    Do đó: 0 = -2(m - 2) + m + 2 ⇔ -2m + 4 + m + 2 = 0 ⇔ m = 6.

    b) Đồ thị hàm số đi qua gốc tọa độ nên O (0; 0) thuộc đồ thị hàm số

    Do đó: 0 = (m - 2).0 + m + 2 ⇔ m + 2 = 0 ⇔ m = -2.

Ví dụ 3: Xác định đường thẳng đi qua hai điểm A (-3; 0) và B (0; 2).

Hướng dẫn:

    Gọi phương trình đường thẳng AB là y = ax + b

    Ta có:

    A(-3;0) ∈ AB ⇒ 0 = a.(-3) + b ⇒ b = 3a

    B(0;2) ∈ AB ⇒ 2 = a.0 + b ⇒ b = 2

    ⇒ a = 2/3

    Vậy phương trình đường thẳng AB là y = (2/3)x + 2.

Ví dụ 4: Cho ba đường thẳng (d₁ ): y = (m² - 1)x + m² - 5 (với m ≠ ±1)

    (d₂ ): y = x + 1; (d₃ ): y = -x + 3

    Xác định m để ba đường thẳng (d₁ ),(d₂ ),(d₃ ) đồng quy

Hướng dẫn:

    Hoành độ giao điểm của hai đường thẳng (d₂) và (d₃) là nghiệm của phương trình:

    x + 1 = -x + 3 ⇔ x = 1 ⇒ y = -1 + 3 = 2

    ⇒ Giao điểm của (d₂) và (d₃) là A (1; 2)

    Để ba đường thẳng (d₁),(d₂),(d₃) đồng quy thì A thuộc (d₁)

    ⇔ 2 = (m² - 1).1 + m² - 5 ⇔ m² = 4 ⇔ m = ±2

    Vậy với m = ±2 thì ba đường thẳng trên đồng quy.

Ví dụ 5 (VD nâng cao): Cho hai đường thẳng

    (d₁ ): y = (2m² + 1)x + 2m - 1

    (d₂ ): y = m²x + m - 2

    với m là tham số

    a) Tìm tọa độ giao điểm I của (d₁ ) và (d₂ ) theo m

    b) Khi m thay đổi, hãy chứng minh điểm I luôn thuộc một đường thẳng cố định.

Hướng dẫn:

    a) Hoành độ giao điểm của (d₁ ) và (d₂ ) là nghiệm của phương trình

    (2m² + 1)x + 2m - 1 = m²x + m - 2

    ⇔(m² + 1)x = -m - 1

    Tung độ giao điểm của (d₁ ) và (d₂ ) là

    y = m²x + m - 2

    b) Ta có:

Bài tập vận dụng

Bài 1: Cho hàm số y = (2m + 1)x - m - 3

    a) Tìm m biết đồ thị hàm số đi qua điểm M (-2; 5)

    b) Tìm m biết đồ thị hàm số cắt trục tung tại điểm có tung độ -3.

Bài 2: Xác định đường thẳng đi qua hai điểm M (-2; 3) và N (1; -3)

Hướng dẫn giải và đáp án

Hướng dẫn:

Bài 1:

    a) Đồ thị hàm số y = (2m + 1)x - m + 3 đi qua điểm M (-2; 5) nên:

    5 = (2m + 1).(-2) - m - 3 ⇔ -4m - 2 - m - 3 = 5 ⇔ m = -2

    Vậy với m = -2 thì đồ thị hàm số đi qua điểm M (-2; 5)

    b) Đồ thị hàm số cắt trục tung tại điểm có tung độ -3 nên điểm A (0; -3) thuộc đồ thị hàm số

    ⇒ -3 = (2m + 1).0 - m + 3 ⇔ -m + 3 = -3 ⇔ m = 6.

    Vậy với m = 6 thì đồ thị hàm số cắt trục tung tại điểm có tung độ -3.

Bài 2:

    Gọi phương trình đường thẳng MN là y = ax + b

    M(-2; 3) ∈ MN ⇒ 3 = -2a + b ⇒ b = 2a + 3 (1)

    N(1; -3) ∈ MN ⇒ -3 = a + b (2)

    Thế (1) vào (2) ta được: -3 = a + 2a + 3 ⇔ 3a = -6 ⇔ a = -2.

    ⇒ b = 2a + 3 = 2.(-2) + 3 = -1.

    Vậy phương trình đường thẳng cần tìm là y = -2x – 1.