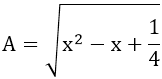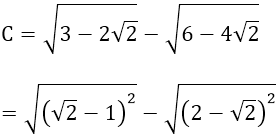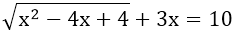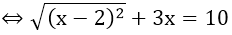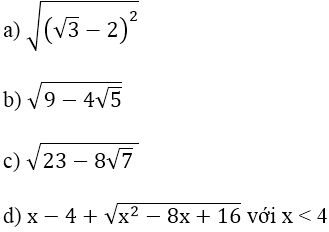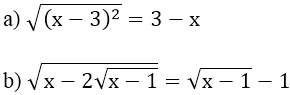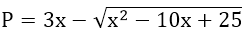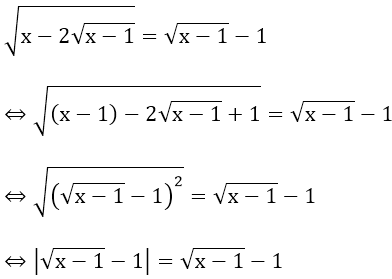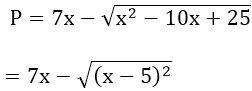Cách Rút gọn biểu thức chứa căn bậc hai cực hay, có đáp án (dạng √(A²))

Phương pháp giải

    Vận dụng hằng đẳng thức:

Ví dụ minh họa

Ví dụ 1: Rút gọn các biểu thức sau:

    a) 

    b) 

    c) 

Hướng dẫn:

    a) 

    Nếu x ≥ 1/2 thì A = x - 1/2

    Nếu x < 1/2 thì A = 1/2 - x

    b) 

    Nếu x ≥ 1 thì B = 3x - (x - 1) = 2x + 1

    Nếu x < 1 thì B = 3x + (x - 1) = 4x - 1.

    c) 

    = √2 - 1| - |2 - √2| = √2 - 1 - (2 - √2) = 2√2 - 3.

Ví dụ 2: Tìm x, biết:

Hướng dẫn:

    ⇔ |x - 2| + 3x = 10 (1)

    Nếu x ≥ 2 thì |x - 2| = x - 2. Khi đó, phương trình (1) trở thành:

    x - 2 + 3x = 10 ⇔ 4x = 12 ⇔ x = 3 (thuộc khoảng đang xét)

    Nếu x < 2 thì |x - 2| = 2 - x. Khi đó, phương trình (1) trở thành:

    2 - x + 3x = 10 ⇔ 2x = 8 ⇔ x = 4 (không thuộc khoảng đang xét)

    Vậy giá trị x thỏa mãn là x = 3.

Bài tập vận dụng

Bài 1: Rút gọn các biểu thức sau:

Bài 2: Tìm x, biết

Bài 3: Cho biểu thức: 

    a) Rút gọn biểu thức đã cho;

    b) Tính giá trị của P khi x = 4.

Hướng dẫn giải và đáp án

Bài 1:

    a)  = |√3 - 2| = 2 - √3

    b)  = |2 - √5| = √5 - 2

    c)  = |4 - √7| = 4 - √7

    d)  với x < 4

     = x - 4 + |x - 4|

    = x - 4 - (x - 4) = 0

Bài 2:

    a) 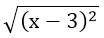 = 2x + 5

    ⇔ |x - 3| = 2x + 5

    Nếu x ≥ 3, phương trình trở thành:

    x - 3 = 2x + 5 ⇔ x = -8 (không thuộc khoảng đang xét)

    Nếu x < 3, phương trình trở thành:

    3 - x = 2x + 5 ⇔ 3x = 2 ⇔ x = 2/3(thuộc khoảng đang xét)

    Vậy phương trình có nghiệm x = 2/3.

    b) 

    Nếu 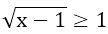 ⇔ x ≥ 2 thì phương trình trở thành:

     ⇔ 0x = 0

    ⇒ Phương trình nghiệm đúng với mọi x ≥ 2

    Nếu 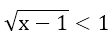 ⇔ x < 2 thì phương trình trở thành:

     ⇔ x = 2 (không thuộc khoảng đang xét)

    Vậy nghiệm của phương trình là x ≥ 2.

Bài 3:

    a) 

    = 7x - |x - 5|

    Nếu x ≥ 5 thì P = 7x - (x - 5) = 6x + 5

    Nếu x < 5 thì P = 7x + (x - 5) = 8x - 5.

    b) Khi x = 4 < 5 thì giá trị của biểu thức P là:

    P = 8.4 - 5 = 27.