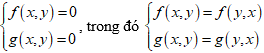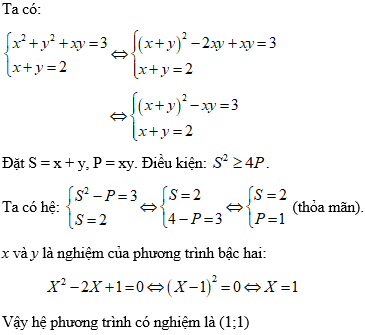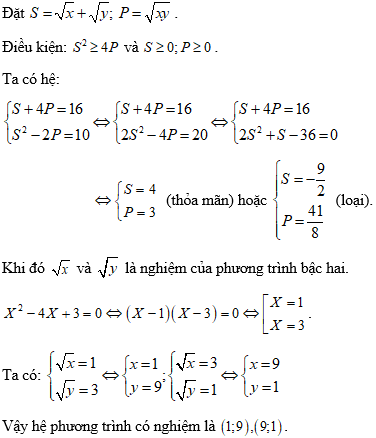Cách giải hệ phương trình đối xứng loại 1 cực hay
Với Cách giải hệ phương trình đối xứng loại 1 cực hay Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải hệ phương trình đối xứng loại 1 cực hay.
Cách giải hệ phương trình đối xứng loại 1 cực hay
A. Phương pháp giải
Hệ phương trình đối xứng loại I theo ẩn x và y làHệ phương trình mà khi ta đổi vai trò của các ẩn x và y thìHệ phương trình vẫn không thay đổi.
Hệ phương trình đối xứng loại I có dạng 
Bước 1: Đặt S = x + y, P = xy. Điều kiện: S2 ≥ 4P.
Bước 2: Biến đổi Hệ phương trình có hai ẩn S, P giải ra S và P (sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Tìm được S và P, khi đó x và y là nghiệm của phương trình bậc hai:
X2 - SX + P = 0
Giải phương trình bậc hai theo ẩn X.
Bước 4: Kết luận nghiệm của hệ phương trình.
Chú ý: Nếu (x0;y0) là nghiệm củaHệ phương trình thì (y0;x0) cũng là nghiệm của hệ phương trình.
B. Ví dụ minh họa
Ví dụ 1: Giải hệ phương trình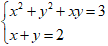 
.
Hướng dẫn:
Ví dụ 2: Giải hệ phương trình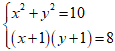 
.
Hướng dẫn:
Vậy hệ phương trình có nghiệm là (1;3), (3;1).
Ví dụ 3: Giải hệ phương trình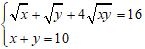 
.
Hướng dẫn:
Điều kiện xác định: x ≥ 0; y ≥ 0.
Bài viết liên quan
- Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay
- Cách tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m của hệ phương trình
- Cách giải hệ phương trình đối xứng loại 2 cực hay
- Cách giải hệ phương trình đặc biệt, nâng cao cực hay
- Phương pháp giải bài toán bằng cách lập hệ phương trình siêu hay, chi tiết
