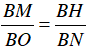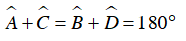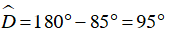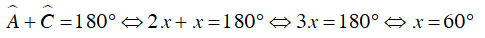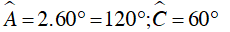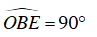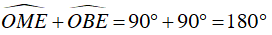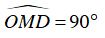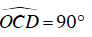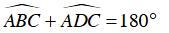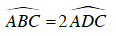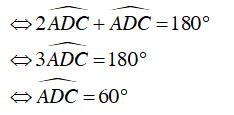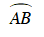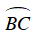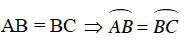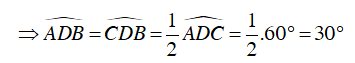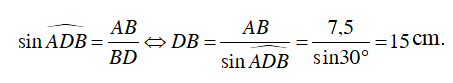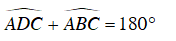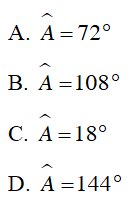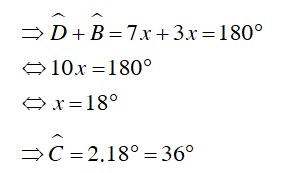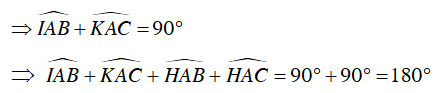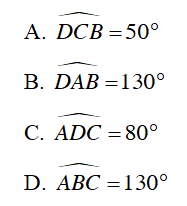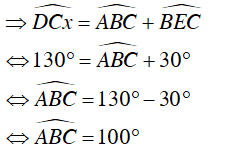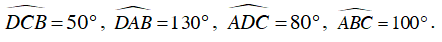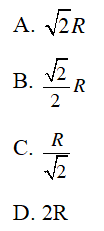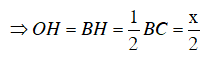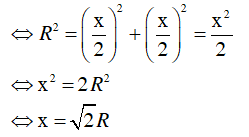Cách chứng minh tứ giác nội tiếp cực hay, chi tiết

A. Phương pháp giải

Đối với chứng minh tứ giác nội tiếp, ta sử dụng các dấu hiệu nhận biết sau:

+ Tứ giác có tổng hai góc đối bằng 180^o.

+ Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

+ Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.

+ Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.

+ Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.

Đối với bài toán tính góc, ta sử dụng các tính chất của tứ giác nội tiếp để tính toán.

B. Ví dụ minh họa

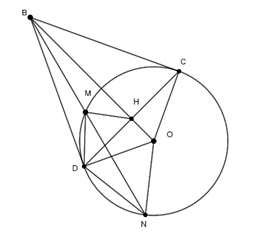
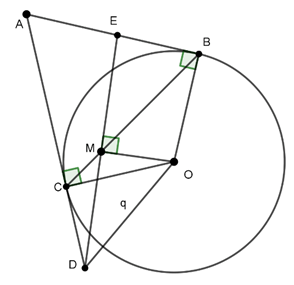
Ví dụ 1 : Qua điểm B nằm ở bên ngoài đường tròn (O), vẽ hai tiếp tuyến BC và BD với đường tròn (O), (C, D là các tiếp điểm). Từ B vẽ cát tuyến BMN (M nằm giữa B và N, tia BN nằm giữa hai tia BC và BO), gọi H là giao điểm của BO và CD.

a. Chứng minh BM.BN = BH.BO.

b. Chứng minh tứ giác OHMN nội tiếp.

Hướng dẫn giải

a. Ta có: BC = BD (tính chất hai tiếp tuyến cắt nhau)

OC = OD (bán kính đường tròn (O))

BO là đường trung trực của CD ⇒ BO ⊥ CD (1)

Xét ΔBMC và ΔBCN có:

 : chung

 (cùng chắn cung  )

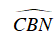
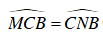
⇒ ΔBMC ∼ ΔBCN (g – g)

⇒  ⇒ BM.BN = BC² (2)

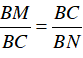
Do (1) ta có △BCO vuông tại C, đường cao CH:

⇒ BC² = BH.BO (hệ thức lượng trong tam giác vuông) (3)

Từ (2) và (3) ⇒ BM.BN = BH.BO.

b. Ta có: BM.BN = BH.BO (chứng minh trên)

⇒ 

ΔBMO và ΔBHN có:

 : chung

⇒ ΔBMO ∼ ΔBHN (c – g – c)

⇒ (hai góc tương ứng)

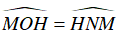
⇒ Tứ giác OHMN nội tiếp (hai góc bằng nhau cùng nhìn một cạnh).

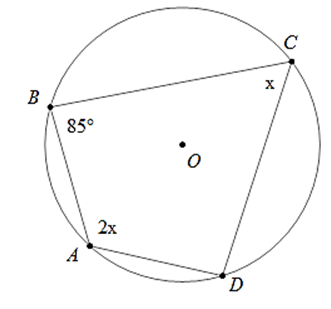
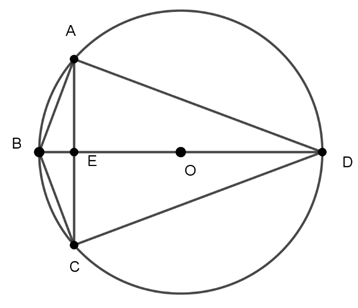
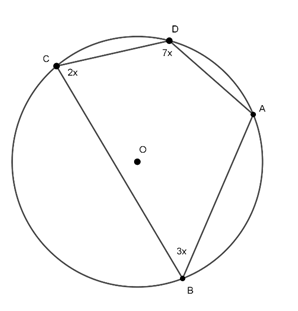
Ví dụ 2 : Tính số đo các góc của tứ giác ABCD

Hướng dẫn giải

Do ABCD là tứ giác nội tiếp nên 

Vì 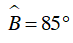 nên 

Ta có: 

⇒ 

Vậy  .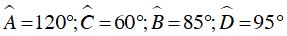

Ví dụ 3 : Cho đường tròn tâm O. Từ điểm A ở bên ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC với đường tròn (B, C là hai tiếp điểm). Trên BC lấy điểm M, vẽ đường thẳng vuông góc với OM tại M, cắt AB và AC lần lượt tại E và D. Chứng minh các tứ giác EBOM và DCMO nội tiếp được trong đường tròn. Xác định tâm các đường tròn đó.

Hướng dẫn giải

– Chứng minh tứ giác EBOM nội tiếp

Có OM ⊥ ME (gt) nên góc 

OB ⊥ BE (BE là tiếp tuyến của (O)) nên góc 

⇒ 

Tứ giác EBOM nội tiếp trong đường tròn đường kính OE.

– Chứng minh tứ giác DCMO nội tiếp

Có OM ⊥ DM (gt) nên góc 

CD ⊥ OC (CĐ là tiếp tuyến của (O)) nên góc 

Nên M, C là hai đỉnh liên tiếp cùng nhìn OD dưới một góc 90^o

⇒ Tứ giác DCMO nội tiếp trong đường tròn đường kính OD.

C. Bài tập trắc nghiệm

Câu 1 : Hình nào sau đây không nội tiếp đường tròn?

A. Hình vuông

B. Hình chữ nhật

C. Hình thoi

D. Hình thang cân

Hướng dẫn giải

Đáp án C

Hình vuông, hình chữ nhật và hình thang cân là các hình nội tiếp đường tròn.

Hình thoi là hình không nội tiếp đường tròn.

Câu 2 : Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính BD. Các đường chéo AC và BD cắt nhau tại E. Biết rằng AB = BC = 7,5cm và 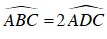 . Tính độ dài đường kính BD.

A. 11cm

B. 12cm

C. 14cm

D. 15cm

Hướng dẫn giải

Đáp án D

Do tứ giác ABCD nội tiếp (O) nên: 

Mà 

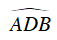
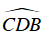
Ta có  là góc nội tiếp chắn 

 là góc nội tiếp chắn 

Mà 

 (hai góc nội tiếp chắn hai cung bằng nhau)

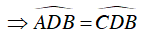
Ta có : 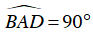 ( góc nội tiếp chắn nửa đường tròn)

⇒ tam giác ABD vuông tại A

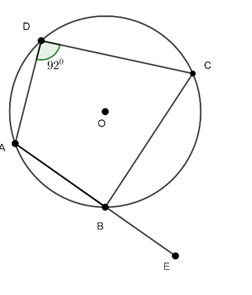
Câu 3 : Cho tứ giác ABCD nội tiếp trong đường tròn. Kéo dài AB về phía B một đoạn BE. Biết 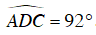 . Số đo góc EBC là:

A.66

B.92

C.70

D.88

Hướng dẫn giải

Đáp án B

Vì tứ giác ABCD nội tiếp nên: 

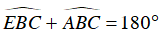
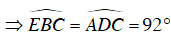
Mà:  (hai góc kề bù)

 .

Câu 4 : Số đo góc A trong hình vẽ

Hướng dẫn giải

Đáp án D

Ta có tứ giác ABCD nội tiếp đường tròn (O)

Mà 

Câu 5 : Cho tam giác nhọn ABC. Đường tròn đường kính BC cắt AB và AC theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD. Tia AH cắt BC tại F. Số tứ giác nội tiếp có trong hình vẽ là:

A. 4

B. 6

C. 7

D. 8

Hướng dẫn giải

Đáp án B

Các tứ giác nội tiếp ADHE, BDHF, FHEC, BDEC, AEFB, ADFC.

Vậy có 6 tứ giác nội tiếp.

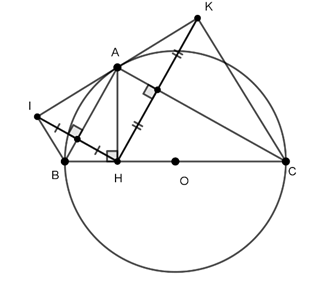
Câu 6 : Cho tam giác ABC vuông tại A, đường cao AH nội tiếp đường tròn (O;R) gọi I và K theo thứ tự là điểm đối xứng của H qua hai cạnh AB và AC. Khẳng định nào sau đây đúng?

A. Tứ giác AHBI nội tiếp đường tròn đường kính AB

B. Tứ giác AHCK nội tiếp đường tròn đường kính AC

C. Ba điểm I, A, K thẳng hàng

D. A, B, C đều đúng.

Hướng dẫn giải

Đáp án D

Ta có AH ⊥ BC 

 ( I đối xứng với H qua AB)

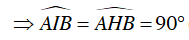
Và 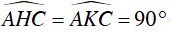 ( K đối xứng với H qua AC)

Xét tứ giác AIBH, có: 

⇒ Tứ giác AIBH nội tiếp đường tròn đường kính AB

Xét tứ giác AKCH, có: 

⇒ Tứ giác AKCH nội tiếp đường tròn đường kính AC

Ta lại có: 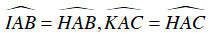 (do tính chất đối xứng)

Mà 

Suy ra ba điểm I, A, K thẳng hàng.

Do đó, cả A, B, C đều đúng.

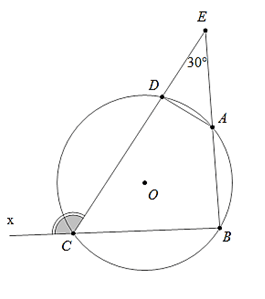
Câu 7 : Cho hình vẽ sau, biết 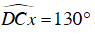 . Đáp án nào sau đây SAI

Hướng dẫn giải

Đáp án D

Ta có: 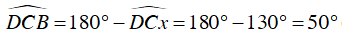 (hai góc kề bù)

Ta lại có : 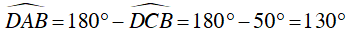 (ABCD là tứ giác nội tiếp đường tròn)

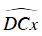
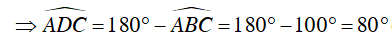
Lại có  là góc ngoài của ΔECB

 (ABCD là tứ giác nội tiếp đường tròn)

Vậy 

Câu 8 : Phát biểu nào sau đây sai ?

A. Tứ giác nội tiếp có 4 đỉnh cùng nằm trên cùng một đường tròn

B. Nếu một tứ giác có tổng hai góc đối bằng 180^o thì tứ giác đó nội tiếp đường tròn.

C. Trong một tứ giác nội tiếp tổng hai góc bất kì bằng 180^o

D. Hinh chữ nhật luôn nội tiếp đường tròn.

Hướng dẫn giải

Đáp án C

Trong tứ giác nội tiếp, tổng hai góc đối mới bằng 180^o .

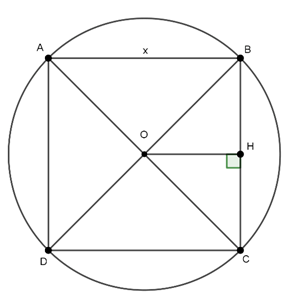
Câu 9 : Cho hình vuông ABCD nội tiếp đường tròn (O;R). Độ dài cạnh hình vuông bằng:

Hướng dẫn giải

Đáp án A

Đặt cạnh góc vuông là x

Ta có hình vuông ABCD nội tiếp (O; R)

Nên O là giao điểm của hai đường chéo, và OA = OB = OC = OD = R.

Kẻ OH vuông góc với BC.

Tam giác OBC vuông cân tại O, có OH ⊥ BC

⇒ H là trung điểm của BC

Xét tam giác OHB vuông tại H, có :

OB² = OH² + BH²

Vậy cạnh hình vuông có độ dài là  .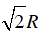

Câu 10 : Các hình nào sau đây nội tiếp đường tròn?

A. Hình thang, hình chữ nhật

B. Hình thang cân, hình bình hành

C. Hình thoi, hình vuông

D. Hình thang cân, hình chữ nhật, hình vuông

Hướng dẫn giải

Đáp án D

Hình thang cân, hình chữ nhật, hình vuông là các hình nội tiếp đường tròn.