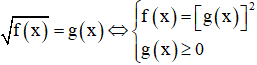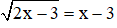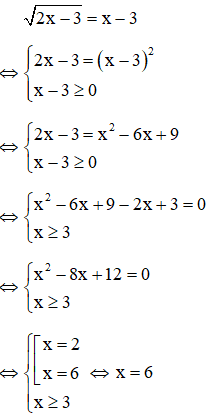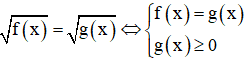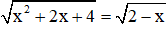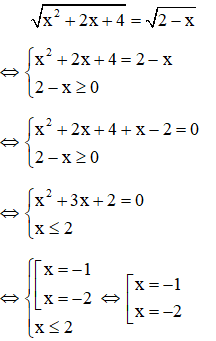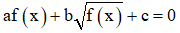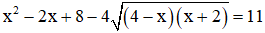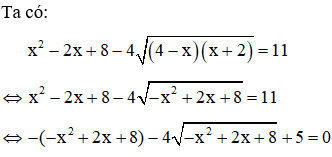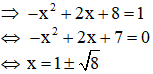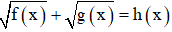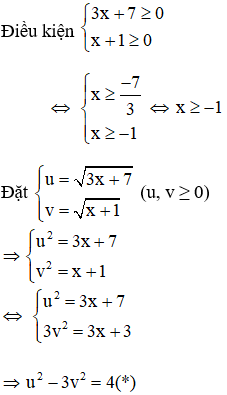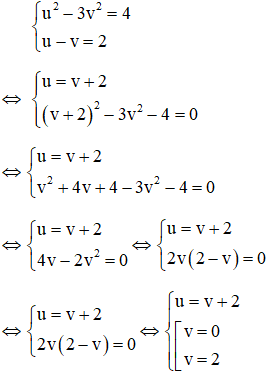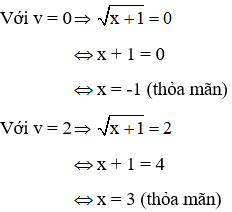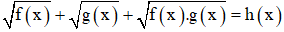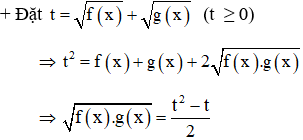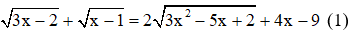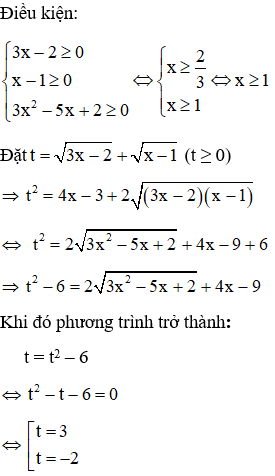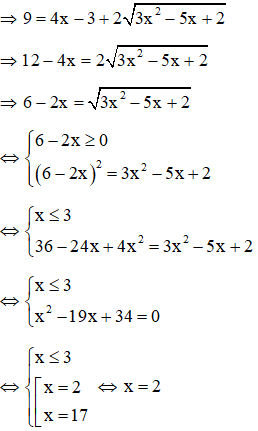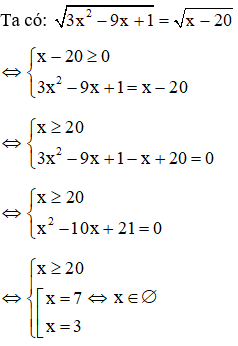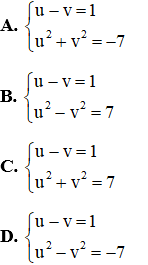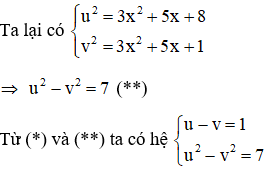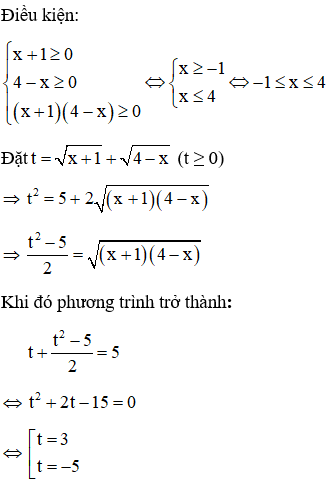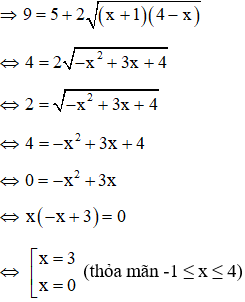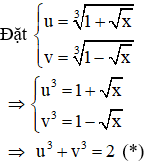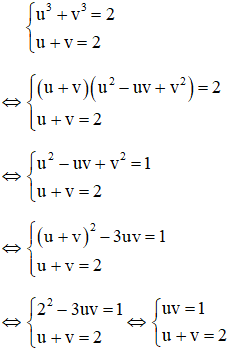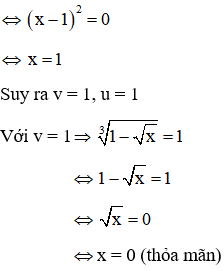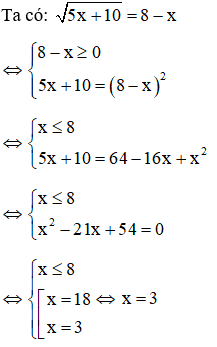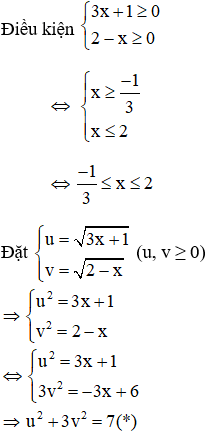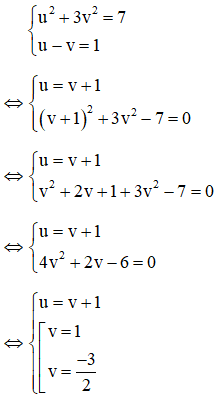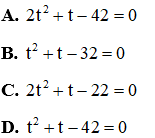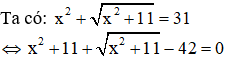Cách giải phương trình chứa căn thức lớp 9 cực hay

A. Phương pháp giải

Để giải phương trình chứa ẩn dưới dấu căn ta tìm cách khử dấu căn. Hai cách hay dùng là:

- Nâng hai vế của phương trình lên một lũy thừa

- Đặt ẩn phụ

Dạng 1: 

Ví dụ: Giải phương trình 

Giải

Vậy phương trình có một nghiệm x = 6

Dạng 2: 

Chú ý: Điều kiện g(x) ≥ 0 có thể thay bởi f(x) ≥ 0

Ví dụ: Giải phương trình 

Giải

Vậy phương trình có hai nghiệm x = -1, x = -2

Dạng 3: 

Đặt 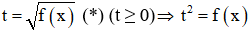. Khi đó phương trình đã cho trở thành: at² + bt + c = 0

Giải phương trình trên tìm t thỏa mãn điều kiện t ≥ 0 rồi sau đó thay vào biểu thức (*) tìm x

Ví dụ: Giải phương trình 

Giải

Đặt 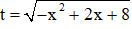 (*) (t ≥ 0) ⇒ t² = -x² + 2x + 8. Khi đó phương trình đã cho trở thành: -t² - 4t + 5 = 0

Phương trình có a + b + c = -1 + (-4) +5 = 0 nên có 2 nghiệm

t = 1( thỏa mãn  t ≥ 0);  t = -5 ( không thỏa mãn  t ≥ 0)

với t = 1 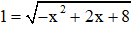 (ĐK: -x² + 2x +8 ≥ 0)

Hai nghiệm tìm được thỏa mãn điều kiện

Vậy phương trình có hai nghiệm x = 1 ± √8

Dạng 4: 

+ Đặt 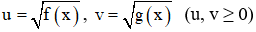 (u, v ≥ 0)

+ Đưa phương trình đã cho về hệ phương trình với hai ẩn là u, v

+ Giải hệ tìm u, v sau đó tìm x

Ví dụ: Giải phương trình 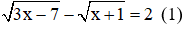 (1)

Giải

Với việc đặt ẩn phụ như trên thì phương trình (1): u – v = 2(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Ta có v = 0 và v = 2 đều thỏa mãn điều kiện v ≥ 0

Vậy phương trình có 2 nghiệm x =-1, x = 3

Dạng 5: 

+ Đưa phương trình đã cho về hệ phương trình với ẩn là t

+ Giải phương trình tìm t, sau đó tìm x

Ví dụ: Giải phương trình 

Giải

Với t = -2 (không thỏa mãn) ⇒ loại

Với t = 3 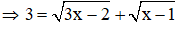 (điều kiện x ≥ 1)

Ta thấy x = 2 thỏa mãn điều kiện x ≥1

Vậy phương trình có 1 nghiệm  x = 2

B. Bài tập

Câu 1: Tổng các nghiệm của phương trình 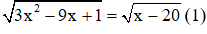 (1) là

A. -3

B. 2

C. 10

D. không tồn tại

Giải

Vậy phương trình vô nghiệm

Đáp án là D

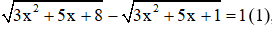
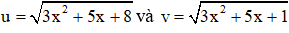
Câu 2: Cho phương trình  (1), nếu đặt  thì phương trình (1) trở thành hệ phương trình nào sau đây

Giải

Đặt  (u, v ≥ 0)thì phương trình (1) trở thành: u – v = 1(*)

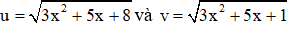
Đáp án đúng là B

Câu 3: Tích các nghiệm của phương trình 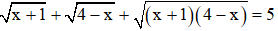 (1) là

A. 0

B. 2

C. 1

D. không tồn tại

Giải

Với t = -5 (không thỏa mãn)⇒ loại

Với t = 3 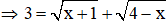 (điều kiện -1≤ x ≤ 4)

Vậy phương trình có 2 nghiệm  x = 0, x = 3

Suy ra tích các nghiệm bằng 0

Đáp án là A

Câu 4: Số nghiệm của phương trình 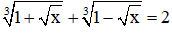 (1) là

A. 1

B. 2

C. 3

D. 4

Giải

Điều kiện: x ≥ 0

Với việc đặt ẩn phụ như trên thì phương trình (1): u + v = 2(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Theo vi-et ta có u, v là nghiệm của phương trình:  x² – 2x + 1 = 0

Vậy phương trình có 1 nghiệm

Đáp án là A

Câu 5: Số nghiệm của phương trình 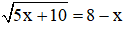 là

A. 0

B. 1

C. 2

D. 3

Giải

Vậy phương trình có một nghiệm

Đáp án là B

Câu 6: Số nghiệm của phương trình 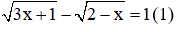 là

A. 1

B. 2

C. 3

D. 4

Giải

Với việc đặt ẩn phụ như trên thì phương trình (1): u – v = 1(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Ta có v = 1 thỏa mãn điều kiện v ≥ 0 nên nhận

Ta có 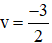 không thỏa mãn điều kiện v ≥ 0 nên loại

Với 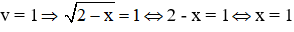 (thỏa mãn)

Vậy phương trình có 1 nghiệm

Đáp án là A

Câu 7: Cho phương trình 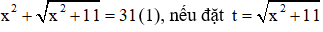  thì phương trình (1) trở thành phương trình nào sau đây

Giải

Đặt . Khi đó phương trình đã cho trở thành: t² + t - 42 = 0

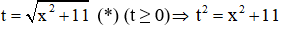
Đáp án đúng là D