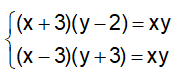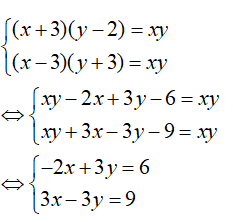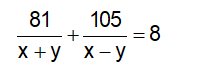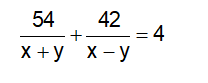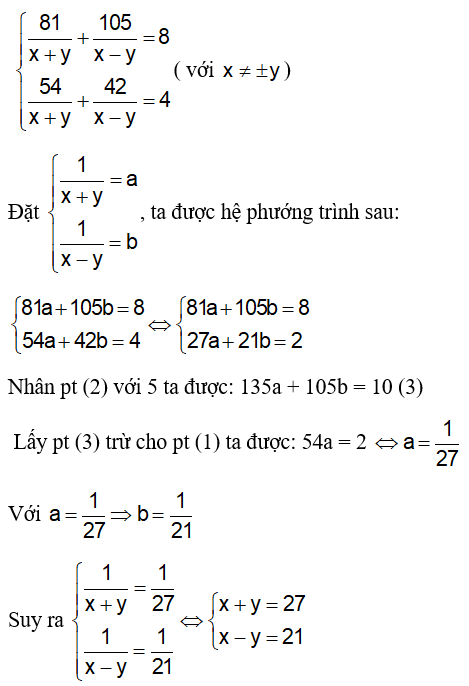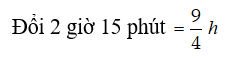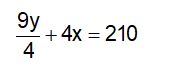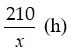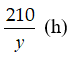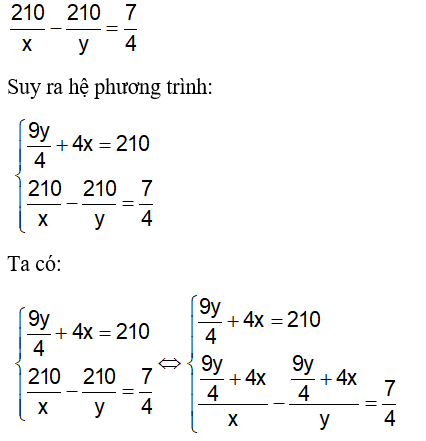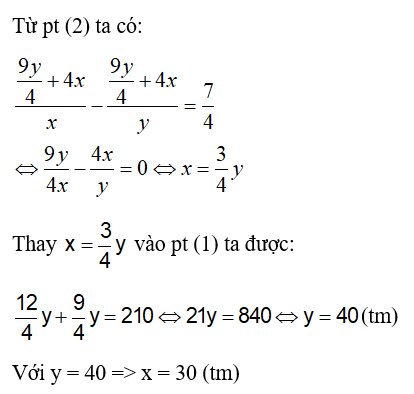Cách giải bài toán chuyển động cực hay | Giải bài toán bằng cách lập hệ phương trình

A. Phương pháp giải

Các công thức cần nhớ:

S = V.T

V_xuôi = V_vật + V_nước, V_ngược = V_vật – V_nước

B. Ví dụ minh họa

Ví dụ 1: Một ca nô dự định đi từ A đến B trong thời gian đã định. Nếu vận tốc ca nô tăng 3km/h thì ca nô đến sớm hơn 2 giờ. Nếu vận tốc ca nô giảm 3km/h thì ca nô đến muộn hơn 3 giờ. Tính chiều dài khúc sông.

Hướng dẫn giải:

Gọi vận tốc dự định của ca nô là x km/h (x >3)

Thời gian dự định đi là y giờ (y >2)

Quãng đường AB là : xy ( km)

Vì vận tốc ca nô tăng 3km/h thì ca nô đến sớm hơn 2 giờ, nên ta có phương trình:

(x +3)(y – 2) = xy

Vì vận tốc ca nô giảm 3km/h thì ca nô đến muộn hơn 3 giờ, nên ta có phương trình:

(x – 3)(y + 3) = xy

Suy ra ta có hệ phương trình:

Ta có:

Cộng vế theo vế của hai phương trình ta được: x = 15 (tm)

Với x = 15 → y = (6 + 2.15): 3 = 12.( tm )

Vậy chiều dài khúc sông là 15 x 12 = 180 km.

Ví dụ 2: Một ca nô chạy trên sông trong 8h, xuôi dòng 81km và ngược dòng 105km. Một lần khác cũng chạy trên khúc sông đó ca nô này chạy trong 4h, xuôi dòng 54km và ngược dòng 42km. Hãy tính vận tốc xuôi và ngược dòng biết vận tốc dòng nước và vận tốc riêng của ca nô là không đổi.

Hướng dẫn giải:

Gọi vận tốc ca no khi nước yên lặng là x km/h.(x>y)

Gọi vận tốc của dòng nước là y km/h ( y > 0)

Vận tốc cano đi xuôi dòng là: x+ y ( km/h)

Vận tốc cano đi ngược dòng là: x – y ( km/h)

Vì ca nô chạy trên sông trong 8h, xuôi dòng 81km và ngược dòng 105km, ta có phương trình:

Vì ca nô chạy trên sông trong 4h, xuôi dòng 54km và ngược dòng 42km, ta có phương trình:

Cộng vế theo vế của hai phương trình trên ta được: 2x = 48 ⇔ x = 24 ( tm )

Với x = 24 → y = 3 ( tm )

Vậy vận tốc xuôi dòng là: 24 + 3 = 27 km/h

Vận tốc ngược dòng là 24 – 3 = 21km/h

Ví dụ 3: Trên quãng đường AB dài 210km tại cùng một thời điểm một xe máy khởi hành từ A đến B và một ô tô khởi hành đi từ B về A sau khi hai xe gặp nhau xe máy đi tiếp 4giờ nữa thì đến B, ô tô đi tiếp 2 giờ15 phút thì đến A. Biết rằng vận tốc của xe máy và ô tô là không đổi. Tính vận tốc của xe máy?

Hướng dẫn giải:

Gọi x, y (km/h) lần lượt là vận tốc của xe máy và ô tô ( x; y > 0)

Quãng đường xe máy đi thêm 4 h và quãng đường ô tô đi trong 2 giờ 15 phút bằng độ dài quãng đường AB nên

Thời gian xe máy đi hết quãng đường AB là 

Thời gian ô tô đi hết quãng đường AB là 

Vì ban đầu hai xe khởi hành cùng 1 lúc nên: