Cách giải phương trình bậc hai chứa tham số cực hay, có đáp án

A. Phương pháp giải

Dạng 3.1: Giải và biện luận phương trình theo tham số m

Bước 1: Xác định các hệ số a; b; c (hoặc a; b'; c).

Bước 2: Giải phương trình theo m:

+) Với giá trị của m mà a = 0, giải phương trình bậc nhất.

+) Với giá trị của m mà a ≠ 0, giải phương trình bậc hai: Tính Δ = b'² - ac (hoặc Δ' = b² - 4ac), xét các trường hợp của Δ chứa tham số và tìm nghiệm theo tham số.

Bước 3: Kết luận.

Biện luận phương trình:

- Phương trình có nghiệm khi:

+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.

+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm.

- Phương trình có một nghiệm khi:

+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.

+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm kép.

- Phương trình có hai nghiệm phân biệt khi: Giá trị của m mà a ≠ 0, phương trình bậc hai có hai nghiệm phân biệt.

Dạng 3.2: Xác định dấu các nghiệm của phương trình

Bước 1: Xác định hệ số.

Bước 2: Tính Δ = b² - 4ac (hoặc Δ' = b² - 4ac) để kiểm tra phương trình có nghiệm hay không.

Bước 3: Trong trường hợp phương trình có nghiệm (Δ ≥ 0 hoặc Δ' ≥ 0), tính tổng S và tích P của hai nghiệm theo định lý Vi-ét để xét dấu các nghiệm của phương trình.

+) Phương trình có hai nghiệm cùng dấu: P > 0.

+) Phương trình có hai nghiệm dương: .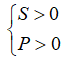

+) Phương trình có hai nghiệm âm: .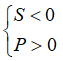

+) Phương trình có hai nghiệm trái dấu: P < 0.

Chú ý: Phương trình có hai nghiệm trái dấu chỉ cần xét P < 0 hoặc a.c < 0.

Bước 4: Kết luận.

Dạng 3.3: Tìm m để phương trình có nghiệm thỏa mãn điều kiện cho trước

Dạng 3.3.1: Tìm m để phương trình có nghiệm thỏa mãn điều kiện về dấu hoặc thỏa mãn đẳng thức, bất đẳng thức liên hệ giữa các nghiệm

Bước 1: Tìm điều kiện a ≠ 0 (nếu cần) và điều kiện để phương trình có nghiệm.

Bước 2: Tính tổng S và tích P của hai nghiệm theo định lý Vi-ét.

Bước 3: Sử dụng hệ thức Vi-ét, kết hợp biến đổi đẳng thức, bất đẳng thức để tìm tham số.

Bước 4: Đối chiếu điều kiện và kết luận.

Dạng 3.3.2: Tìm tham số m để phương trình có một nghiệm là x₀.

Bước 1: Thay giá trị x₀ vào phương trình để tìm tham số.

Bước 2: Thay giá trị của tham số vào phương trình hoặc hệ thức Vi-ét để tìm nghiệm còn lại.

Bước 3: Kết luận.

Dạng 3.3.3: Tìm giá trị của tham số để hai phương trình có ít nhất một nghiệm chung.

Bước 1: Tìm điều kiện để các phương trình có nghiệm.

Bước 2: Tìm nghiệm chung và tìm tham số: Có thể giả sử x₀ là nghiệm chung, lập hệ phương trình trình hai ẩn (x₀ và tham số) và giải hệ phương trình.

Bước 3: So sánh với điều kiện và kết luận.

B. Các ví dụ điển hình

Ví dụ 1: Giải phương trình x² - 2x + 1 - m² = 0 với m là tham số, m ≠ 0.

Lời giải

Chọn A

Ví dụ 2: Cho phương trình x² + √7x + 1 = 0. Khẳng định nào sau đây là đúng?

Lời giải

Chọn B

Ví dụ 3: Số các giá trị nguyên của tham số m để phương trình x² - 2x + m = 0 có hai nghiệm phân biệt x₁; x₂ sao cho x₁².x₂² ≤ 4 là:.

Lời giải

Chọn B

Ví dụ 4: Phương trình bậc hai mx² + (2m + 1)x + 3 = 0 có một nghiệm là x = -1. Giá trị của m và nghiệm còn lại là:

Lời giải

Chọn A

Ví dụ 5: Cho hai phương trình bậc hai x² + 2x + m = 0 (1) và x² + mx + 2 = 0 (2) (với m là tham số). Tìm m để hai phương trình có ít nhất một nghiệm chung.

Lời giải

Chọn B