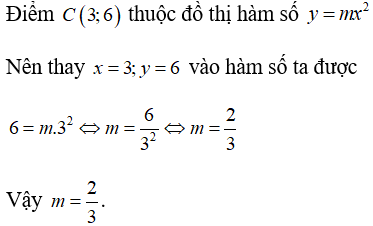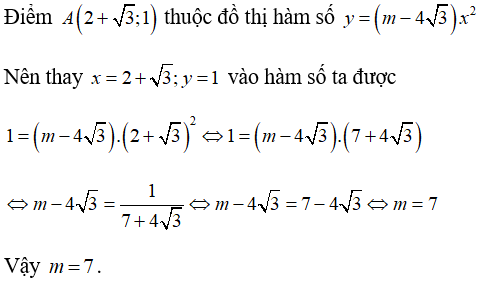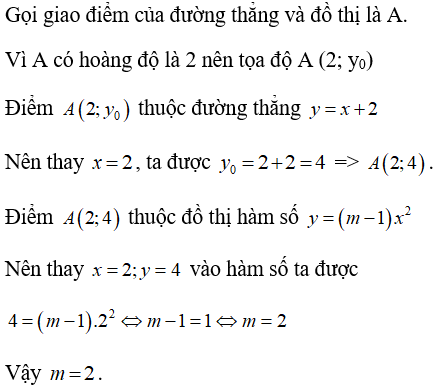Các bài toán về tham số của hàm số y = ax2 cực hay, có đáp án
Với Các bài toán về tham số của hàm số y = ax2 cực hay, có đáp án Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Các bài toán về tham số của hàm số y = ax2 cực hay, có đáp án.
Các bài toán về tham số của hàm số y = ax2 cực hay, có đáp án
A. Phương pháp giải
Cho hàm số y = ax2(a ≠ 0).
Tính chất của hàm số và đồ thị.
- Nếu a > 0:
+ Hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Hàm số đạt GTNN bằng 0 tại x = 0.
+ Đồ thị hàm số nằm phía trên trục hoành, có điểm O là điểm thấp nhất của đồ thị.
- Nếu a < 0:
+ Hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
+ Hàm số đạt GTLN bằng 0 tại x = 0.
+ Đồ thị hàm số nằm phía dưới trục hoành, có điểm O là điểm cao nhất của đồ thị.
Tìm tham số khi biết một điểm thuộc đồ thị
Bước 1: Tìm tọa độ (x; y) của một điểm thuộc đồ thị hàm số (nếu cần).
Bước 2: Thay các giá trị x; y vào hàm số, giải phương trình để tìm tham số.
Bước 3: Kết luận.
B. Các ví dụ điển hình
Ví dụ 1:Cho hàm số y = mx2(với m là tham số, m ≠ 0). Giá trị của m để đồ thị hàm số đi qua điểm C(3; 6) là:
Lời giải
Chọn A
Ví dụ 2:Điểm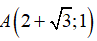 
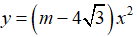
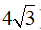
thuộc đồ thị hàm số 
(với m là tham số, m ≠ 
). Giá trị m là:
Lời giải
Chọn D
Ví dụ 3:Đường thẳng y = x + 2 cắt đồ thị của hàm số y = (m - 1)x2 (với m là tham số, m ≠ 1) tại điểm có hoành độ bằng 2. Giá trị của tham số m là:
Lời giải
Chọn C
Bài viết liên quan
- Tính giá trị của hàm số tại một điểm cho trước cực hay, có đáp án
- Xét tính đồng biến, nghịch biến của hàm số cực hay, có đáp án
- Cách giải các bài toán về đường thẳng y = ax + b cực hay, có đáp án
- Cách tìm tọa độ giao điểm của parabol và đường thẳng cực hay, có đáp án
- Cách biện luận số giao điểm của đường thẳng và parabol cực hay, có đáp án
