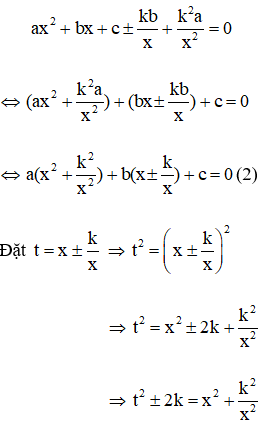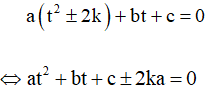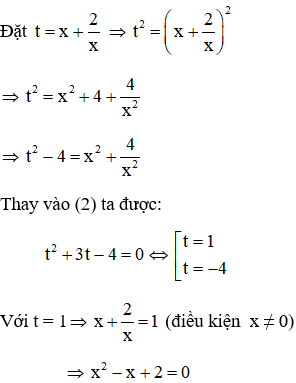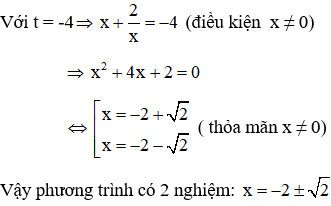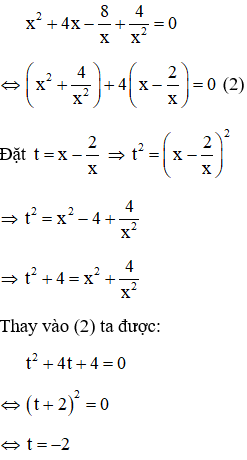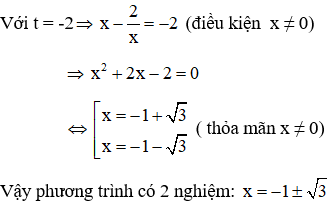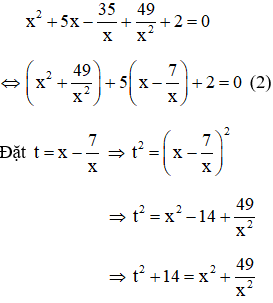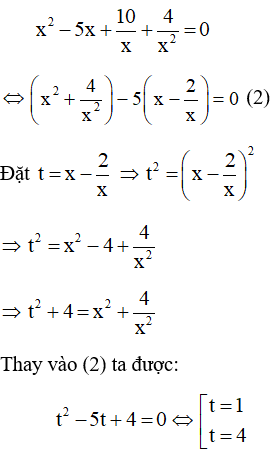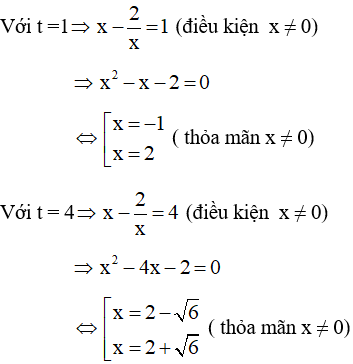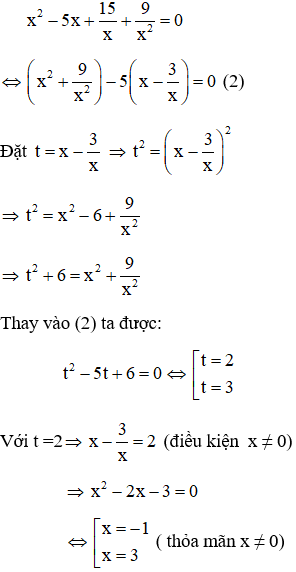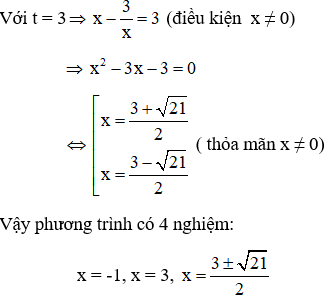Cách giải phương trình bậc bốn dạng ax^4 + bx^3 + cx ^2 ± kbx + k^2a = 0
Với Cách giải phương trình bậc bốn dạng ax^4 + bx^3 + cx ^2 ± kbx + k^2a = 0 Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải phương trình bậc bốn dạng ax^4 + bx^3 + cx ^2 ± kbx + k^2a = 0.
Cách giải phương trình bậc bốn dạng ax4 + bx3 + cx2 ± kbx + k2a = 0
A. Phương pháp giải
Vì x = 0 không là nghiệm của phương trình (1) nên chia hai vế của (1) cho x2 ta được
Thay vào phương trình (2) ta có:
Giải phương trình trên tìm t rồi sau đó tìm x
B. Bài tập
Câu 1: Giải phương trình x4 + 4 = -3x3 – 6x
Giải
Phương trình x4 + 4 = -3x3 – 6x ⇔ x4 + 3x3 + 6x + 4 = 0 (1)
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
(phương trình vô nghiệm vì ∆ = (-1)2 – 4.1.2 = -7 < 0)
Câu 2: Giải phương trình x4 + 4x3 – 8x + 4 = 0 (1)
Giải
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
Câu 3: Giải phương trình x4 + 5x3 + 2x2 – 35x + 49 = 0 (1)
Giải
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
Thay vào (2) ta được: t2 + 5t + 16 = 0
Phương trình trên có ∆ = 52 – 4.1.16 = 25 – 64 = -39 < 0 nên phương trình vô nghiệm
Vậy phương trình (1) vô nghiệm
Câu 4: Giải phương trình x4 + 4 = 5x(x2 – 2)
Giải
Phương trình (1) ⇔ x4 + 4 = 5x3-10x ⇔ x4 - 5x3 + 10x + 4 = 0
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được:
Vậy phương trình có 4 nghiệm: x = -1, x = 2, x = 2 ± √6
Câu 5: Giải phương trình x4 + 9 = 5x(x2 – 3)
Giải
Phương trình (1) ⇔ x4 + 9 = 5x3 - 15x ⇔ x4 - 5x3 + 15x + 9 = 0
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
Bài viết liên quan
- Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)(x + b)(x + c)(x + d) = 0)
- Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)4 + (x + b)4 = c)
- Cách giải phương trình chứa căn thức lớp 9 cực hay
- Cách giải phương trình có chứa dấu giá trị tuyệt đối hay, chi tiết
- Giải bài toán bằng cách lập phương trình – Dạng toán về quan hệ giữa các số, tìm số tự nhiên
