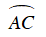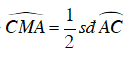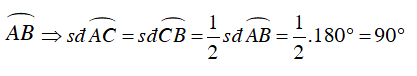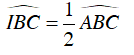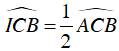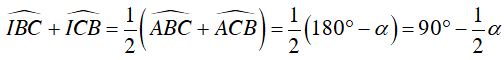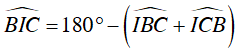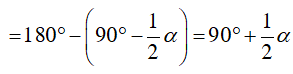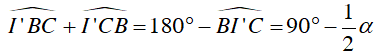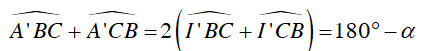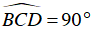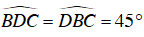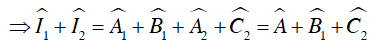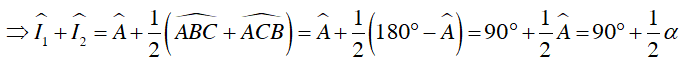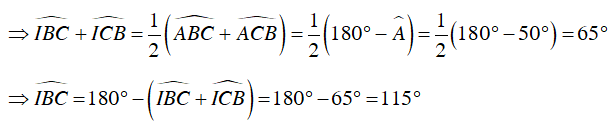Cách giải bài tập Quỹ tích cung chứa góc cực hay, chi tiết

A. Phương pháp giải

1. Bài toán quỹ tích cung chứa góc:

Với đoạn thẳng AB và góc α (0^o < α < 180^o) cho trước thì quỹ tích các điểm M thỏa mãn 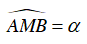 là hai cung chứa góc α dựng trên đoạn AB.

Chú ý:

- Hai cung chứa góc α dựng trên đoạn AB là hai cung tròn đối xứng nhau qua AB.

- Hai điểm A, B được coi là thuộc quỹ tích

- Khi α = 90^o thì quỹ tích các điểm nhìn đoạn AB cho trước dưới một góc vuông là đường tròn đường kính AB.

2. Cách giải bài toán quỹ tích

Muốn chứng minh quỹ tích (tập hợp) các điểm M thỏa mãn tính chất T là một hình H nào đó, ta phải chứng minh hai phần:

Phần thuận: Mọi điểm có tính chất T đều thuộc hình H.

Phần đảo: Mọi điểm thuộc hình H đều có tính chất T

Kết luận: Quỹ tích (hay tập hợp) các điểm M có tính chất T là hình H.

Trong trường hợp, ta cần dự đoán hình H trước khi chứng minh

B. Ví dụ minh họa

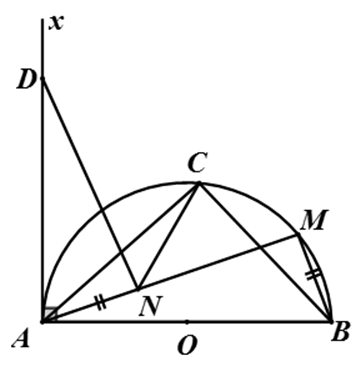
Ví dụ 1 : Cho nửa đường tròn (O) đường kính AB, có C là điểm chính giữa của cung AB. M là một điểm chuyển động trên cung BC . Lấy điểm N thuộc đoạn AM sao cho AN = MB. Vẽ tiếp tuyến Ax với nửa đường tròn; D là điểm thuộc Ax sao cho AD = AB .

a) Chứng minh rằng ΔMNC vuông cân.

b) Chứng minh rằng DN ⊥ AM

c) Tìm quỹ tích điểm N.

Hướng dẫn giải

a) Xét ΔANC và ΔBMC, ta có:

AN = BM (gt)

 (hai góc nội tiếp cùng chắn cung CM)

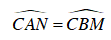
AC = CB ( Do C là điểm chính giữa cung AB)

⇒ ΔANC = ΔBMC (c.g.c)

⇒ CN = CM (hai cạnh tương ứng) (1)

Ta có: 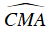 là góc nội tiếp chắn cung 

⇒ 

Do C là điểm chính giữa cung 

⇒  (2)

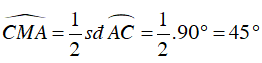
Từ (1) và (2) suy ra ΔMNC vuông cân tại C.

b) Xét ΔAND và ΔBMA có:

+ AD = AB (gt)

+  (góc tạo bởi tia tiếp tuyến với dây cung và góc nội tiếp cùng chắn cung AM)

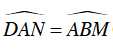
+ AN = BM (gt)

⇒ ΔAND = ΔBMA (c.g.c)

Do đó  .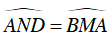

Mà 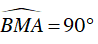 (góc nội tiếp chắn nửa đường tròn)

Suy ra 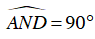 hay DN ⊥ AM.

c) * Phần thuận:

Vì 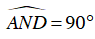 ⇒ N nhìn đoạn AD cố định dưới một góc 90^o nên N thuộc đường tròn đường kính AD.

Giới hạn: Nếu M ≡ A thì N ≡ C, nếu M ≡ C thì N ≡ A do đó quỹ tích điểm N là cung nhỏ AN của đường tròn đường kính AD (cung này thuộc nửa mặt phẳng bờ là đường thẳng Ax có chứa nửa đường tròn (O)).

* Phần đảo:

Lấy M’ là một điểm thuộc đường tròn đường kính AD.

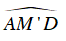
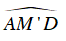
Khi đó,  là góc nội tiếp chắn nửa đường tròn

⇒  = 90^o

Kết luận: Quỹ tích điểm N là đường tròn đường kính AD.

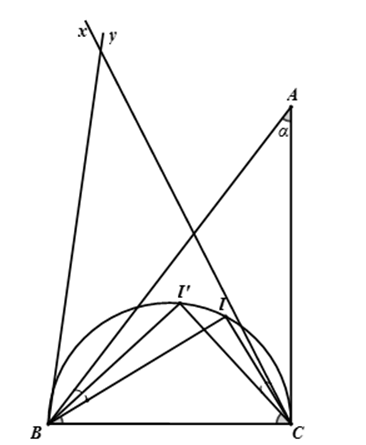
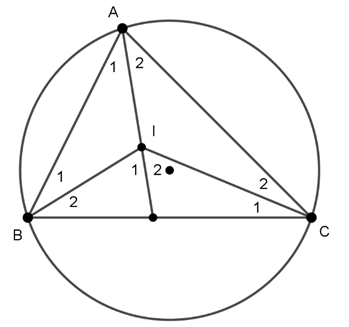
Ví dụ 2 : Cho ΔABC có cạnh BC cố định và 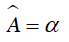 không đổi (0^o < α < 180^o). Tìm quỹ tích tâm I của đường tròn nội tiếp ΔABC

Hướng dẫn giải

* Phần thuận:

Vì I là tâm đường tròn nội tiếp ΔABC nên BI là phân giác của 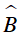 , do đó: 

CI là phân giác 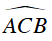 , do đó: 

Suy ra: 

Trong ΔBCI có: 

Suy ra điểm I nhìn đoạn thẳng BC cố định dưới một góc 90o + 1/2 α nên I thuộc cung chứa góc 90o + 1/2 α dựng trên đoạn thẳng BC (trên cùng một nửa mặt phẳng bờ BC có chứa điểm A).

* Phần đảo:

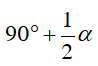
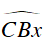
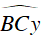
Lấy I’ thuộc cung chứa góc  nói trên. Vẽ các tia Bx và Cy sao cho BI’ là tia phân giác của  và CI’ là tia phân giác của góc  . Hai tia Bx và Cy cắt nhau tại A’.

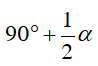
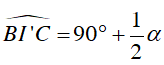
Vì I’ thuộc cung chứa góc  dựng trên đoạn BC nên:  .

Do đó: 

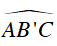
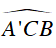
Vì BI’ là phân giác của  và CI’ là phân giác của  nên

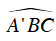
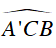
Mặt khác I’ là giao điểm các tia phân giác của  và  nên I’ là tâm đường tròn nội tiếp ΔA'BC

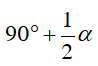
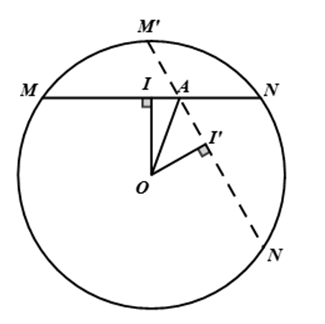
Kết luận: Quỹ tích tâm I của đường tròn nội tiếp ΔABC là cung chứa góc  dựng trên đoạn BC.

Ví dụ 3 : Cho đường tròn (O) và điểm A cố định nằm trong đường tròn . Một đường thẳng d quay quanh điểm A cắt đường tròn (O) tại hai điểm M và N. Tìm quỹ tích trung điểm I của MN.

Hướng dẫn giải

* Phần thuận:

Vì I là trung điểm của dây MN suy ra OI ⊥ MN Do đó 

Vì điểm I nhìn đoạn OA cố định dưới góc 90^o nên I nằm trên đường tròn đường kính OA.

* Phần đảo:

Lấy điểm I’ bất kỳ thuộc đường tròn đường kính OA.

Nối AI’ cắt đường tròn (O) tại M’ và N’

Vì I’ thuộc đường tròn đường kính OA nên 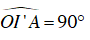 hay OI' ⊥ M'N'

Suy ra I’ là trung điểm của M’N’ (theo quan hệ giữa đường kính và dây cung)

Kết luận: Quỹ tích trung điểm I của MN là đường tròn đường kính OA.

C. Bài tập trắc nghiệm

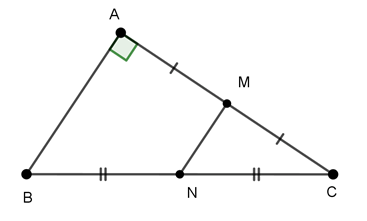
Câu 1 : Cho hai điểm B và C cố định, lấy điểm A bất kì sao cho tam giác ABC vuông tại A. Gọi N và M lần lượt là trung điểm BC và AC. Tìm quỹ tích điểm M .

A. Đường tròn đường kính NC

B. Đường tròn đường kính BC

C. Đường tròn đường kính BN.

D. Đáp án khác

Hướng dẫn giải

Đáp án A

Xét tam giác ABC vuông tại A, có:

M là trung điểm của AC

N là trung điểm của BC

Suy ra MN là đường trung bình của tam giác ABC

⇒ MN//AB

Mà AB ⊥ AC

⇒ MN ⊥ AC ⇒ 

Ta có BC cố định, N là trung điểm của BC nên NC cố định.

Khi đó quỹ tích điểm M là đường tròn đường kính NC.

Câu 2 : Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn trên dây AC kéo dài lấy điểm D sao cho CD = CB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.

A. Hai cung chứa góc 45^o dựng trên đoạn BC

B. Hai cung chứa góc 45^o dựng trên đoạn AB

C. Đường tròn đường kính BC

D. Đường tròn đường kính AB

Hướng dẫn giải

Đáp án B

Ta có 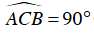 ( góc nội tiếp chắn nửa đường tròn)

⇒ BC ⊥ AD

⇒ 

Ta lại có: BC = CD

Suy ra tam giác BCD vuông cân tại C

⇒ 

Khi đó điểm D nhìn đoạn thẳng cố định AB dưới một góc không đổi

Vậy quỹ tích điểm M là hai cung chứa góc dựng trên đoạn AB.

Câu 3 : Cho hai điểm B và C cố định. Lấy A là điểm bất kì sao cho tam giác ABC cân tại A. Gọi H là trực tâm của tam giác ABC. Tìm quỹ tích điểm H.

A. Đường tròn đường kính BC

B. Đường trung trực của đoạn thẳng BC

C. Đường tròn tâm B, bán kính BC

D. Đường tròn tâm C, bán kính BC

Hướng dẫn giải

Đáp án B

Vì H là trực tâm của tam giác ABC nên AH ⊥ BC

Lại có tam giác ABC là tam giác cân tại A nên đường cao AH đồng thời là đường trung trực.

Suy ra: H nằm trên đường trung trực của đoạn thẳng BC.

Câu 4 : Cho tam giác ABC có cạnh BC cố định và góc 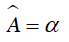 không đổi. Tìm quỹ tích giao điểm của ba đường phân giác trong của tam giác đó.

A. Cung chứa góc α dựng trên đoạn BC

B. Hai cung chứa góc α dựng trên đoạn BC

C. Đường tròn đường kính BC

D. Hai cung chứa góc 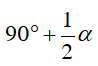 dựng trên đoạn BC

Hướng dẫn giải

Đáp án D

Gọi I là giao điểm của ba đường phân giác trong của tam giác ABC.

Xét tam giác ABI, có: 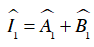 ( tính chất góc ngoài của tam giác)

Xét tam giác ACI, có: 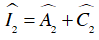 ( tính chất góc ngoài của tam giác)

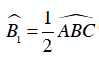
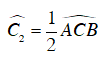
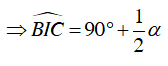
Ta có:  (BI là phân giác trong góc ABC)

 (CI là phân giác trong góc ACB)

 không đổi

Điểm I nhìn đoạn BC cố định dưới một góc 

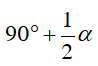
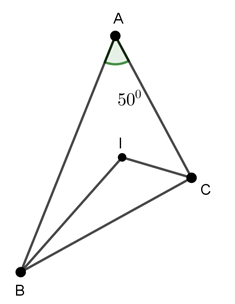
Vậy quỹ tích điểm I là hai cung chứa góc  dựng trên đoạn BC.

Câu 5 : Cho tam giác ABC có BC cố định và góc A bằng 50^o . Gọi I là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm I

A. Một cung chứa góc 115^o dựng trên đoạn BC

B. Một cung chứa góc 115^o dựng trên đoạn AC

C. Hai cung chứa góc 115^o dựng trên đoạn AB

D. Hai cung chứa góc 115^o dựng trên đoạn BC

Hướng dẫn giải

Đáp án D

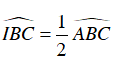
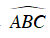
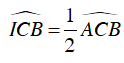
Ta có:  (BI là phân giác của  )

 (CI là phân giác của  )

Khi đó quỹ tích điểm I là hai cung chứa góc 115^o dựng trên đoạn BC.

Câu 6 : Cho các hình thoi ABCD có cạnh AB cố định . Tìm quỹ tích giao điểm của hai đường chéo của hình thoi đó .

A. Quỹ tích điểm O là 2 cung chứa góc 120^o dựng trên AB

B. Quỹ tích điểm O là nửa đường tròn đường kính AB, trừ hai điểm A và B

C. Quỹ tích điểm O là 2 cung chứa góc 60^o dựng trên AB

D. Quỹ tích điểm O là 2 cung chứa góc 30^o dựng trên AB

Hướng dẫn giải

Chọn B.

Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường

Suy ra AO ⊥ BO ⇒ 

Ta có 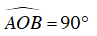 không đổi mà AB cố định

⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B.

Câu 7 : Cho tứ giác ABCD có 2 đường chéo vuông góc với nhau tại O. Biết 2 điểm A và B cố định, 2 điểm C và D di chuyển. Tìm quỹ tích điểm O

A. Đường tròn đường kính AB.

B. Đường tròn bán kính AB.

C. Đường tròn bán kính AB/2

D. Đường tròn đường kính 2AB

Hướng dẫn giải

Đáp án A

Ta có: AC vuông góc BD tại O nên: 

Suy ra: quỹ tích điểm O là đường tròn đường kính AB.

Câu 8 : Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là

A. Đường tròn đường kính AB

B. Nửa đường tròn đường kính AB

C. Đường tròn đường kính AB/2

D. Đường tròn bán kính AB

Hướng dẫn giải

Đáp án A

Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

Câu 9 : Với đoạn thẳng AB và góc α(0^o < α < 180^o) cho trước thì quỹ tích các điểm M thỏa mãn 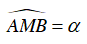 là

A. Hai cung chứa góc α dựng trên đoạn AB . Hai cung này không đối xứng nhau qua AB

B. Hai cung chứa góc α dựng trên đoạn AB và không lấy đoạn AB

C. Hai cung chứa góc α dựng trên đoạn AB . Hai cung này đối xứng nhau qua AB

D. Một cung chứa góc α dựng trên đoạn AB

Hướng dẫn giải

Đáp án C

Với đoạn thẳng AB và góc α(0^o < α < 180^o) cho trước thì quỹ tích các điểm thỏa mãn 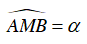 là hai cung chứa góc α dựng trên đoạn AB.

Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB . Hai điểm A, B được coi là thuộc quỹ tích.

Câu 10 : Cho đoạn thẳng BC cố định. Lấy điểm A bất kì sao cho tam giác ABC cân tại. Tìm quỹ tích điểm A?

A. Đường tròn tâm B bán kính BC.

B. Đường tròn tâm C bán kính BC.

C. Đường trung trực của đoạn thẳng BC.

D. Đường tròn đường kính BC.

Hướng dẫn giải

Đáp án C

Do tam giác ABC cân tại A nên AB = AC

Suy ra, A thuộc đường trung trực của đoạn thẳng BC