Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án

Với Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án.

731

Tải tài liệu

« Trang trước

Trang sau »

Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án

A. Phương pháp giải

bài toán về diện tích hình học

Bước 1: Lập phương trình.

- Chọn ẩn và đặt điều kiện cho ẩn (nếu có).

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình.

Bước 3: So sánh với điều kiện và kết luận.

Một số công thức tính diện tích thường gặp:

Diện tích tam giác: 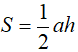Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án - Toán lớp 9 (a là độ dài cạnh đáy, h là độ dài đường cao ứng với cạnh đáy).

Diện tích hình vuông: S = a² (a là độ dài cạnh góc vuông).

Diện tích hình chữ nhật: S = ab (a, b là chiều dài, chiều rộng của hình chữ nhật).

Diện tích hình tròn: S = πR² (R là bán kính của hình tròn).

Hỏi đáp VietJack

B. Các ví dụ điển hình

Ví dụ 1: Một mảnh đất hình chữ nhật có diện tích 720m², nếu tăng chiều dài 6m và giảm chiều rộng 4m thì diện tích của mảnh vườn không đổi. Tính các kích thước của mảnh vườn đó.