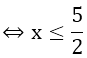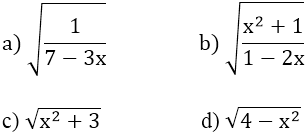Tìm điều kiện để √A có nghĩa
Với Tìm điều kiện để √A có nghĩa Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Tìm điều kiện để √A có nghĩa.
Tìm điều kiện để √A có nghĩa
Phương pháp giải
√A có nghĩa ⇔ A ≥ 0
có nghĩa ⇔ A > 0
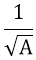
Ví dụ minh họa
Ví dụ 1: Tìm x để căn thức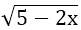 
có nghĩa
Hướng dẫn:
có nghĩa ⇔ 5 - 2x ≥ 0 ⇔ -2x ⇔ -5
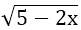
Ví dụ 2: Tìm x để căn thức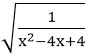 
có nghĩa
Hướng dẫn:
có nghĩa
có nghĩa
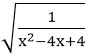
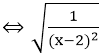
⇔ (x - 2)2 > 0 ⇔ x ≠ 2.
Bài tập vận dụng
Bài 1: Với giá trị nào của x thì mỗi căn thức sau có nghĩa:
Bài 2: Có bao nhiêu giá trị nguyên của x để biểu thức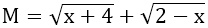 
có nghĩa?
Hướng dẫn giải và đáp án
Hướng dẫn:
Bài 1:
a)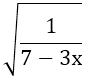 
có nghĩa ⇔ 7 - 3x > 0 ⇔ x < 7/3
b)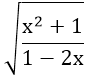 
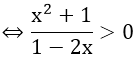
có nghĩa 
⇔ 1 - 2x > 0 (do x2 + 1 > 0)
⇔ x < 1/2
c) Vì x2 + 3 > 0 với mọi x nên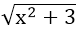 
có nghĩa với mọi x.
d)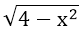 
có nghĩa ⇔ 4 - x2 ≥ 0 ⇔ x2 ≤ 4
⇔|x| ≤ 2 ⇔ -2 ≤ x ≤ 2.
Bài 2:
có nghĩa khi:
⇔ -4 ≤ x ≤ 2
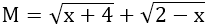
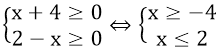
Vì -4 ≤ x ≤ 2; x ∈ Z nên x ∈ {-4; -3; -2; -1; 0; 1; 2}
Vậy có 7 giá trị nguyên của x để biểu thức M có nghĩa.
Bài viết liên quan
- Cách So sánh căn bậc hai số học cực hay, có đáp án
- Cách Rút gọn biểu thức chứa căn bậc hai cực hay, có đáp án (dạng √(A2))
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa căn
- Liên hệ giữa phép nhân, phép chia với phép khai phương
- Cách biến đổi đơn giản biểu thức chứa căn bậc hai cực hay, có đáp án
