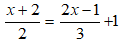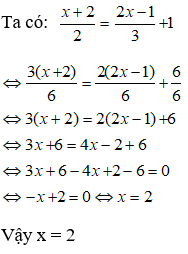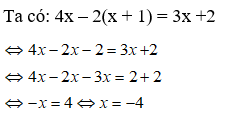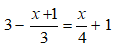Bài 44: Phương trình bậc nhất một ẩn và cách giải

A. Lý thuyết

1. Định nghĩa về phương trình bậc nhất một ẩn

Ví dụ:

Phương trình 2x - 3 = 0 là phương trình bậc nhất ẩn x.

Phương trình y - 4 = 2 là phương trình bậc nhất ẩn y.

2. Hai quy tắc biến đổi phương trình

a) Quy tắc chuyển vế

Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

Ví dụ: Giải phương trình x + 3 = 0

Hướng dẫn:

Ta có x + 3 = 0 ⇔ x = - 3. (chuyển hạng tử + 3 từ vế trái sang vế phải và đổi thành - 3 ta được x = - 3 )

b) Quy tắc nhân với một số

Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.

Ví dụ: Giải phương trình x/2 = - 2.

Hướng dẫn:

Ta có x/2 = - 2 ⇔ 2.x/2 = - 2.2 ⇔ x = - 4. (nhân cả hai vế với số 2 ta được x = - 4 )

3. Cách giải phương trình bậc nhất một ẩn

Cách giải:

    Bước 1: Chuyển vế ax = - b.

    Bước 2: Chia hai vế cho a ta được: x = - b/a.

   Bước 3: Kết luận nghiệm: S = { - b/a }.

Ta có thể trình bày ngắn gọn như sau:

ax + b = 0 ⇔ ax = - b ⇔ x = - b/a.

Vậy phương trình có tập nghiệm là S = { - b/a }.

Ví dụ: Giải các phương trình sau

a) 2x - 3 = 3.

b) x - 7 = 4.

Hướng dẫn:

a) Ta có: 2x - 3 = 3 ⇔ 2x = 6 ⇔ x = 6/2 = 3.

Vậy phương trình đã cho có tập nghiệm S = { 3 }.

b) Ta có x - 7 = 4 ⇔ x = 4 + 7 ⇔ x = 11.

Vậy phương trình đã cho có tập nghiệm là S = { 11 }

4. Bài tập tự luyện

Bài 1: Giải các phương trình sau:

a) 7x - 35 = 0

b) 4x - x - 18 = 0

c) x - 6 = 8 - x

Hướng dẫn:

a) Ta có: 7x - 35 = 0 ⇔ 7x = 35 ⇔ x = 35/7 = 5.

Vậy phương trình có nghiệm là x = 5.

b) Ta có: 4x - x - 18 = 0 ⇔ 3x - 18 = 0 ⇔ 3x = 18 ⇔ x = 18/3 = 6.

Vậy phương trình có nghiệm là x = 6.

c) Ta có: x - 6 = 8 - x ⇔ 2x = 14 ⇔ x = 14/2 = 7.

Vậy phương trình có nghiệm là x = 7.

Bài 2:

a) Tìm giá trị của m sao cho phương trình sau nhận x = - 5 làm nghiệm: 2x - 3m = x + 9.

b) Tìm giá trị của m, biết rằng phương trình: 5x + 2m = 23 nhận x = 2 làm nghiệm

Hướng dẫn:

a) Phương trình 2x - 3m = x + 9 có nghiệm là x = - 5

Khi đó ta có: 2.( - 5 ) - 3m = - 5 + 9 ⇔ - 10 - 3m = 4

⇔ - 3m = 14 ⇔ m = - 14/3.

Vậy m = - 14/3 là giá trị cần tìm.

b) Phương trình 5x + 2m = 23 có nghiệm là x = 2

Khi đó ta có: 5.2 + 2m = 23 ⇔ 2m = 23 - 10

⇔ 2m = 13 ⇔ m = 13/2.

Vậy m = 13/2 là giá trị cần tìm

B. Bài tập trắc nghiệm

Bài 1: Nghiệm của phương trình 2x - 1 = 3 là ?

   A. x = - 2.   B. x = 2.

   C. x = 1.   D. x = - 1.

Đáp án

Ta có: 2x - 1 = 3 ⇔ 2x = 1 + 3 ⇔ 2x = 4

⇔ x = 4/2 ⇔ x = 2.

Vậy nghiệm của phương trình là x = 2.

Chọn đáp án B.

Bài 2: Nghiệm của phương trình y/2 + 3 = 4 là?

   A. y = 2.   B. y = - 2.

   C. y = 1.   D. y = - 1.

Đáp án

Ta có: y/2 + 3 = 4 ⇔ y/2 = 4 - 3 ⇔ y/2 = 1

⇔ y = 2.1 ⇔ y = 2.

Vậy nghiệm của phương trình là y = 2.

Chọn đáp án A.

Bài 3: Giá trị của m để phương trình 2x = m + 1 có nghiệm x = - 1 là ?

   C. m = - 3   D. m = 2.

Đáp án

Phương trình 2x = m + 1 có nghiệm x = - 1

Khi đó ta có: 2.( - 1 ) = m + 1 ⇔ m + 1 = - 2 ⇔ m = - 3.

Vậy m = - 3 là giá trị cần tìm.

Chọn đáp án C.

Bài 4: Tập nghiệm của phương trình - 4x + 7 = - 1 là?

   A. S = { 2 }.   B. S = { - 2 }.

   C. S = { 3/2 }.   D. S = { 3 }.

Đáp án

Ta có: - 4x + 7 = - 1 ⇔ - 4x = - 1 - 7 ⇔ - 4x = - 8

⇔ x = - 8/ - 4 ⇔ x = 2.

Vậy phương trình có tập nghiệm là S = { 2 }.

Chọn đáp án A.

Bài 5: x = 1/2 là nghiệm của phương trình nào sau đây?

   A. 3x - 2 = 1.

   B. 2x - 1 = 0.

   C. 4x + 3 = - 1.

   D. 3x + 2 = - 1.

Đáp án

+ Đáp án A: 3x - 2 = 1 ⇔ 3x = 3 ⇔ x = 1 → Loại.

+ Đáp án B: 2x - 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2 → Chọn.

+ Đáp án C: 4x + 3 = - 1 ⇔ 4x = - 4 ⇔ x = - 1 → Loại.

+ Đáp án D: 3x + 2 = - 1 ⇔ 3x = - 3 ⇔ x = - 1 → Loại.

Chọn đáp án B.

Bài 6: Giải phương trình:

   A. x = 2     B. x = 1

   C. x = -2     D. x = -1

Bài 7: Giải phương trình: 4x - 2(x + 1) = 3x + 2

   A. x = 2     B. x = -3

   C. x = - 4     D. x = 5

Bài 8: Tìm số nghiệm của phương trình sau: x + 2 - 2(x + 1) = -x

   A. 0     B.1

   C. 2     D. Vô số

Bài 9: Tìm tập nghiệm của phương trình sau: 2(x + 3) - 5 = 4 – x

   A. S = {1}     B. S = 1

   C. S = {2}     D. S = 2

Bài 10: Phương trình sau có 1 nghiệm 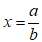 là phân số tối giản. Tính a + b

   A. 22     B. 17

   C. 27     D. 20