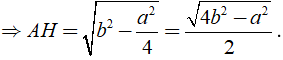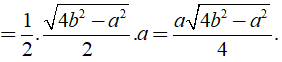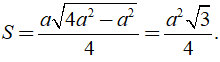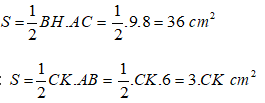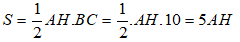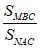Toán lớp 8 Bài 39: Diện tích tam giác
Lý thuyết tổng hợp Toán học lớp 8 Bài 39: Diện tích tam giác chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 39: Diện tích tam giác
A. Lý thuyết
1. Định lý
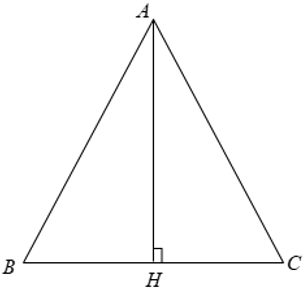
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
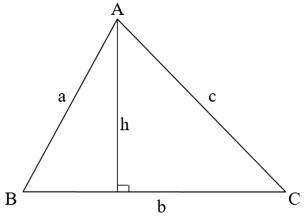
Ta có: S = 1/2b.h.
Ví dụ: Cho tam giác Δ ABC có độ dài đường cao h = 4 cm, đáy BC = 5 cm. Tính diện tích Δ ABC ?
Hướng dẫn:
Diện tích của tam giác Δ ABC là SABC = 1/2BC.h = 1/24.5 = 10 ( cm2 ).
2. Hệ quả
Nếu Δ ABC vuông (áp dụng với hình bên trên) thì diện tích của tam giác bằng một nửa của tích hai cạnh góc vuông.
Tổng quát : S = 1/2a.c (áp dụng với kí hiệu ở hình trên).
Ví dụ: Cho Δ ABC vuông tại A có cạnh AB = 3 cm;AC = 4 cm. Tính diện tích của tam giác Δ ABC ?
Hướng dẫn:
Diện tích của tam giác ABC là SABC = 1/2AB.AC = 1/2.3.4 = 6( cm2 )

3. Bài tập tự luyện
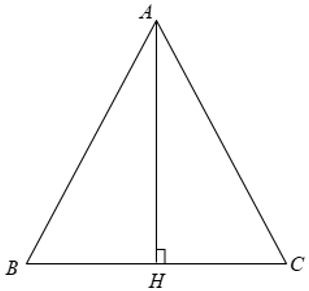
Bài 1: Tính diện tích của một tam giác cân có cạnh đáy là a, cạnh bên bằng b. Từ đó hãy tính diện tích của một tam giác đều có cạnh bằng a.
Hướng dẫn:
Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC = 1/2BC = a/2
Khi đó ta có: SABC = 1/2AH.BC = 1/2.a.AH
Áp dụng định lý Py – to – go ta có:
AC2 = AH2 + HC2 ⇒ AH = √ (AC2 - HC2) .
Khi đó SABC = 1/2AH.BC
Do đó diện tích của tam giác đều các cạnh bằng a là
Bài 2: Cho Δ ABC cân tại A có BC = 30( cm ), đường cao AH = 20 ( cm ). Tính đường cao ứng với cạnh bên của tam giác cân đó.
Hướng dẫn:
Xét Δ ABC cân tại A có BC = 30( cm )
⇒ BH = CH = 15( cm ).
Áp dụng đinh lý Py – ta – go ta có:
AB = √ (AH2 + HB2) = √ (202 + 152) = 25( cm )
Kẻ BK ⊥ AC, giờ ta phải tính BK = ?
Ta có : SABC = 1/2AH.BC = 1/2.20.30 = 300 ( cm2 )
Mặt khác SABC = 1/2BK.AC = 1/2.BK.25
Do đó, ta có 1/2BK.25 = 300 ⇔ BK = (2.300)/25 = 24( cm ).
B. Bài tập trắc nghiệm
Bài 1: Cho Δ ABC, có đường cao AH = 2/3BC thì diện tích tam giác là ?
A. 2/5BC2. B. 2/3BC2.
C. 1/3BC2. D. 1/3BC.
Đáp án
Ta có diện tích của tam giác: S = 1/2b.h.
Trong đó: b là độ dài cạnh đáy, h là độ dài đường cao
Khi đó ta có : S = 1/2AH.BC = 1/2.2/3BC.BC = 1/3BC2.
Chọn đáp án C.
Bài 2: Δ ABC có đáy BC = 6cm, đường cao AH = 4cm. Diện tích Δ ABC là ?
A. 24cm2 B. 12cm2
C. 24cm. D. 14cm2
Đáp án
Ta có diện tích Δ ABC là S = 1/2AH.BC = 1/2.6.4 = 12( cm2 ).
Chọn đáp án B.
Bài 3: Cho Δ ABC vuông tại A, có đáy BC = 5cm và AB = 4cm. Diện tích Δ ABC là ?
A. 12cm2 B. 10cm
C. 6cm2 D. 3cm2
Đáp án
Áp dụng định lý Py – to – go ta có: AB2 + AC2 = BC2 ⇒ AC = √ (BC2 - AB2)
⇒ AC = √ (52 - 42) = 3cm.
Khi đó SABC = 1/2AB.AC = 1/2.4.3 = 6( cm2 )
Chọn đáp án C.
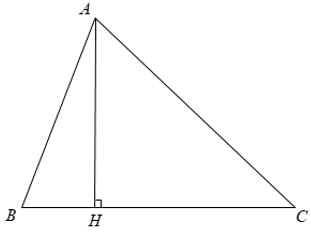
Bài 4: Cho Δ ABC, đường cao AH. Biết AB = 15cm, AC = 41cm, HB = 12cm. Diện tích của Δ ABC là ?
A. 234( cm2 ) B. 214( cm2 )
C. 200( cm2 ) D. 154( cm2 )
Đáp án
Áp dụng định lý Py – to – go ta có:
+ Xét Δ ABH có AH2 + BH2 = AB2 ⇒ AH = √ (AB2 - BH2)
⇒ AH = √ (152 - 122) = 9 ( cm ).
+ Xét Δ ACH có AC2 = AH2 + HC2 ⇒ HC = √ (AC2 - AH2)
⇒ HC = √ (412 - 92) = 40 ( cm ).
Khi đó SABC = 1/2AH.BC = 1/2AH( HB + HC ) = 1/2.9.( 12 + 40 ) = 234 ( cm2 ).
Chọn đáp án A.
Bài 5: Cho tam giác ABC có AB = 6cm, AC = 8cm. Hai đường cao xuất phát từ đỉnh B và C là BH và CK. Biết BH = 9cm. Tính CK
A. 12cm B. 15cm
C. 9cm D. 8cm
Đáp án
Diện tích tam giác ABC là:
Suy ra: 3CK = 36 nên CK = 12cm
Chọn đáp án A
Bài 6: Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8 cm. Tính độ dài đường cao xuất phát từ A?
A. 4cm B. 4,5cm
C. 4,8cm D. 5cm
Đáp án
Áp dụng định lí Pytago vào tam giác ABC ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100
Suy ra: BC = 10cm
Diện tích tam giác ABC là:
Gọi AH là đường cao xuất phát từ đỉnh A của tam giác ABC ,
Khi đó:
Suy ra: 5AH = 24 ⇔ AH = 4,8cm
Chọn đáp án C
Bài 7: Cho tam giác ABC có đường cao AH = 6cm, diện tích tam giác ABC là 30 cm2. Gọi M là trung điểm của BC. Tính diện tích tam giác ABM
A. 10cm2 B. 12cm2
C. 20cm2 D. 15cm2
Đáp án
Chọn đáp án D
Bài 8: Cho tam giác ABC có diện tích bằng 40cm2. Gọi M là trung điểm của AC . Tính diện tích tam giác ABM?
A. 10cm2 B. 20cm2
C. 25cm2 D. Chưa thể kết luận
Đáp án
Chọn đáp án B
Bài 9: Cho tam giác ABC có AB = 4cm và AC = 7cm. Gọi BH và CK theo thứ tự là đường vuông góc từ đỉnh B và C của tam giác. Tính BH/CK ?
A. 4/7 B. 7/4
C. 4/3 D. Đáp án khác
Đáp án
Chọn đáp án A
Bài 10: Cho tam giác ABC có AB = 6cm và AC = 8cm . Gọi M và N theo thứ tự là trung điểm của AC và AB. Tính tỉ số
A. 1/2 B. 2
C. 1 D. Chưa thể kết luận
Đáp án
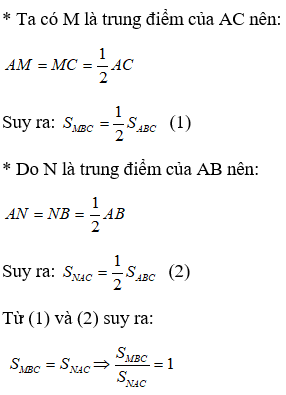
Chọn đáp án C