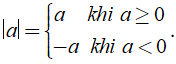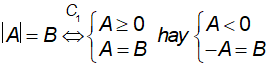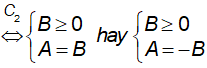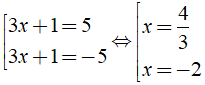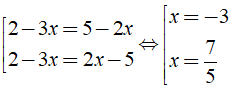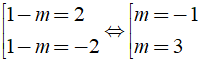Bài 54: Phương trình chứa dấu giá trị tuyệt đối

A. Lý thuyết

1. Nhắc lại về giá trị tuyệt đối

Giá trị tuyệt đối của số a, được kí hiệu là | a |, ta định nghĩa như sau:

Ví dụ: Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau:

a) A = | x - 1 | + 3 - x khi x ≥ 1.

b) B = 3x - 1 + | - 2x | khi x < 0.

Hướng dẫn:

a) Khi x ≥ 1 ta có x - 1 ≥ 0 nên | x - 1 | = x - 1

Do đó A = | x - 1 | + 3 - x = x - 1 + 3 - x = 2.

b) Khi x < 0 ta có - 2x > 0 nên | - 2x | = - 2x

Do đó B = 3x - 1 + | - 2x | = 3x - 1 - 2x = x - 1.

2. Giải một số phương trình chứa dấu giá trị tuyệt đối

a) Phương pháp chung

Bước 1: Áp dụng định nghĩa giá trị tuyệt đối để loại bỏ dấu giá trị tuyệt đối

Bước 2: Rút gọn hai vế của phương trình, giải phương trình

Bước 3: Chọn nghiệm thích hợp trong từng trường hợp đang xét

Bước 4: Kết luận nghiệm

b) Một số dạng cơ bản

Dạng

hoặc

Dạng | A | = | B | ⇔ A = B hay A = - B.

Dạng phương trình có chứa nhiều dấu giá trị tuyệt đối

+ Xét dấu các biểu thức chứa ẩn nằm trong dấu GTTĐ.

+ Chia trục số thành nhiều khoảng sao cho trong mỗi khoảng, các biểu thức nói trên có dấu xác định.

+ Xét từng khoảng, khử các dấu GTTĐ, rồi giải PT tương ứng trong trường hợp đó.

+ Kết hợp các trường hợp đã xét, suy ra số nghiệm của PT đã cho.

Ví dụ: Giải bất phương trình | 4x | = 3x + 1

Hướng dẫn:

Ta có | 4x | = 3x + 1

+ Với x ≥ 0 ta có | 4x | = 4x

Khi đó phương trình trở thành 4x = 3x + 1

⇔ 4x - 3x = 1 ⇔ x = 1.

Giá trị x = 1 thỏa mãn điều kiện x ≥ 0, nên 1 là một nghiệm của phương trình đã cho

+ Với x < 0 ta có | 4x | = - 4x

Khi đó phương trình trở thành - 4x = 3x + 1

⇔ - 4x - 3x = 1 ⇔ - 7x = 1 ⇔ x = - 1/7.

Giá trị x = - 1/7 thỏa mãn điều kiện x < 0, nên - 1/7 là một nghiệm cần tìm.

Vậy phương trình đã cho có tập nghiệm là S = { - 1/7;1 }

3. Bài tập tự luyện

Bài 1: Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau:

a) A = 3x + 2 + | 5x | với x > 0.

b) A = | 4x | - 2x + 12 với x < 0.

c) A = | x - 4 | - x + 1 với x < 4

Hướng dẫn:

a) Với x > 0 ⇒ | 5x | = 5x

Khi đó ta có: A = 3x + 2 + | 5x | = 3x + 2 + 5x = 8x + 2

Vậy A = 8x + 2.

b) Ta có: x < 0 ⇒ | 4x | = - 4x

Khi đó ta có: A = | 4x | - 2x + 12 = - 4x - 2x + 12 = 12 - 6x

Vậy A = 12 - 6x.

c) Ta có: x < 4 ⇒ | x - 4 | = 4 - x

Khi đó ta có: A = | x - 4 | - x + 1 = 4 - x - x + 1 = 5 - 2x.

Vậy A = 5 - 2x

Bài 2: Giải các phương trình sau:

a) | 2x | = x - 6

b) | - 5x | - 16 = 3x

c) | 4x | = 2x + 12

d) | x + 3 | = 3x - 1

Hướng dẫn:

a) Ta có: | 2x | = x - 6

+ Với x ≥ 0, phương trình tương đương: 2x = x - 6 ⇔ x = - 6.

Không thỏa mãn điều kiện x ≥ 0.

+ Với x < 0, phương trình tương đương: - 2x = x - 6 ⇔ - 3x = - 6 ⇔ x = 2.

Không thỏa mãn điều kiện x < 0.

Vậy phương trình đã cho vô nghiệm.

b) Ta có: | - 5x | - 16 = 3x

+ Với x ≥ 0, phương trình tương đương: 5x - 16 = 3x ⇔ 2x = 16 ⇔ x = 8

Thỏa mãn điều kiện x ≥ 0

+ Với x < 0, phương trình tương đương: - 5x - 16 = 3x ⇔ 8x = - 16 ⇔ x = - 2

Thỏa mãn điều kiện x < 0

Vậy phương trình đã cho có tập nghiệm là S = { - 2;8 }

c) Ta có: | 4x | = 2x + 12

+ Với x ≥ 0, phương trình tương đương: 4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6

Thỏa mãn điều kiện x ≥ 0

+ Với x < 0, phương trình tương đương: - 4x = 2x + 12 ⇔ - 6x = 12 ⇔ x = - 2

Thỏa mãn điều kiện x < 0

Vậy phương trình đã cho có tập nghiệm là S = { - 2;6 }

d) Ta có: | x + 3 | = 3x - 1

+ Với x ≥ - 3, phương trình tương đương: x + 3 = 3x + 1 ⇔ - 2x = - 2 ⇔ x = 1.

Thỏa mãn điều kiện x ≥ - 3

+ Với x < - 3, phương trình tương đương: - x - 3 = 3x + 1 ⇔ - 4x = 4 ⇔ x = - 1

Không thỏa mãn điều kiện x < - 3

Vậy phương trình đã cho có tập nghiệm là S = { 1 }

B. Bài tập trắc nghiệm

Bài 1: Biểu thức A = | 4x | + 2x - 1 với x < 0, rút gọn được kết quả là?

   A. A = 6x - 1

   B. A = 1 - 2x

   C. A = - 1 - 2x

   D. A = 1 - 6x

Bài 2: Tập nghiệm của phương trình: | 3x + 1 | = 5

   A. S = { - 2 }

   B. S = { 4/3 }

   C. S = { - 2;4/3 }

   D. S = { Ø }

Bài 3: Tập nghiệm của phương trình |2 - 3x| = |5 - 2x| là?

   B. S = { - 3;7/5 }

   C. S = { 0;7/5 }

   D. S = { - 3;1 }

Bài 4: Giá trị m để phương trình | 3 + x | = m có nghiệm x = - 1 là?

   A. m = 2   B. m = - 2

   C. m = 1   D. m = - 1

Bài 5: Giá trị của m để phương trình | x - m | = 2 có nghiệm là x = 1 ?

   A. m ∈ { 1 }

   B. m ∈ { - 1;3 }

   C. m ∈ { - 1;0 }

   D. m ∈ { 1;2 }

Bài 6: Rút gọn biểu thức A = |2x + 4| + 2(x - 3) với x > 0

A. 4x - 2 B. 3 – 4x C. -10 D. 4x -10

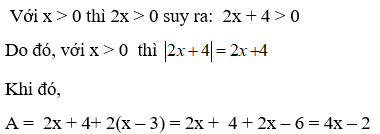
Chọn đáp án A

Bài 7: Với x > 2 thì |3 - (2x - 1)| bằng ?

A. 2x + 4 B. 2x - 4 C. 2x - 1 D. 2x – 2

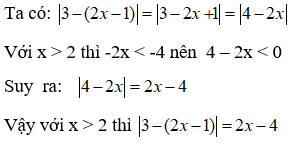
Chọn đáp án B

Bài 8: Tìm tất cả các giá trị của x thỏa mãn: |6 - 2(x + 2)| = 2 - 2x

A. x = 1 B. x < 1 C. x ≤ 1 D. x > 1

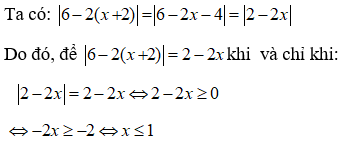
Chọn đáp án C

Bài 9: Giải phương trình sau: |x + 1| = 2x + 7

A. x = 8 hoặc x = -2 B. x = 2 C. x = 2 hoặc x = 8 D. x = 8

Bài 10: Giải phương trình |2 - (x + 4)| = |2x - 3(x + 2)|

A. x = 3 hoặc x = -4 B. x = 1 hoặc x = -2 C. x = -4 D. x = 4 và x = 2

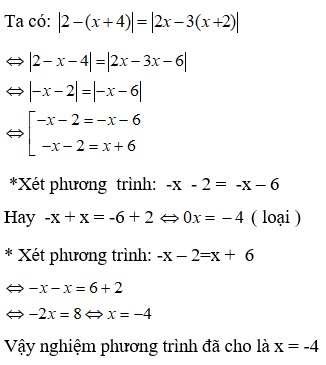
Chọn đáp án C