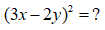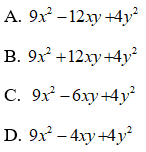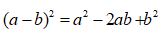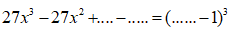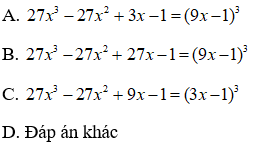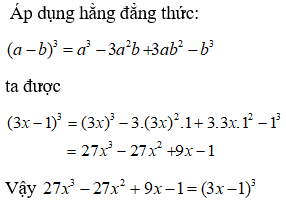Toán lớp 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp)
Lý thuyết tổng hợp Toán học lớp 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp) chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 4: Những hằng đẳng thức đáng nhớ (tiếp)
A. Lý thuyết
1. Lập phương của một tổng
Với A, B là các biểu thức tùy ý, ta có: ( A + B )3 = A3 + 3A2B + 3AB2 + B3.
Ví dụ:
a) Tính ( x + 2 )3.
b) Viết biểu thức x3 + 3x2 + 3x + 1 dưới dạng lập phương của một tổng.
Hướng dẫn:
a) Ta có ( x + 2 )3 = x3 + 3.x2.2 + 3x.22 + 23 = x3 + 6x2 + 12x + 8.
b) Ta có x3 + 3x2 + 3x + 1 = x3 + 3x2.1 + 3x.12 + 13 = ( x + 1 )3.
2. Lập phương của một hiệu.
Với A, B là các biểu thức tùy ý, ta có: ( A - B )3 = A3 - 3A2B + 3AB2 - B3.
Ví dụ :
a) Tính ( 2x - 1 )3.
b) Viết biểu thức x3 - 6x2y + 12xy2 - 8y3 dưới dạng lập phương của một hiệu.
Hướng dẫn:
a) Ta có: ( 2x - 1 )3 = ( 2x )3 - 3.( 2x )2.1 + 3( 2x ).12 - 13 = 8x3 - 12x2 + 6x - 1
b) Ta có : x3 - 6x2y + 12xy2 - 8y3 = ( x )3 - 3.x2.2y + 3.x.( 2y )2 - ( 2y )3 = ( x - 2y )3
B. Bài tập trắc nghiệm
Bài 1: Giá trị của x thỏa mãn 2x2 - 4x + 2 = 0 là ?
A. x = 1. B. x = - 1.
C. x = 2. D. x = - 2.
Đáp án
Ta có 2x2 - 4x + 2 = 0 ⇔ 2( x2 - 2x + 1 ) = 0 ( 1 )
Áp dụng hằng đẳng thức ( a - b )2 = a2 - 2ab + b2
Khi đó ta có ( 1 ) ⇔ 2( x - 1 )2 = 0 ⇔ x - 1 = 0 ⇔ x = 1.
Chọn đáp án A.
Bài 2: 
Đáp án
Áp dụng hằng đẳng thức đáng nhớ: 
Ta được:
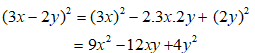
Chọn đáp án A
Bài 3: Điền vào chỗ chấm:
Đáp án
Chọn đáp án C
Bài 4: Rút gọn biểu thức: A = (x – 2y).(x2 + 2xy + y2) - (x + 2y). (x2 – 2xy + y2)
A. 2x3 B. -16y3
C. 16y3 D. –2x3
Đáp án
Áp dụng hằng đẳng thức:
a3 – b3 = (a – b).(a2 + ab + b2) và a3 + b3 = (a + b).(a2 – ab + b2) ta được:
A = (x – 2y). (x2 + 2xy + y2) - (x + 2y). (x2 – 2xy + y2)
A = x3 – (2y)3 - [x3 + (2y)3]
A = x3 – 8y3 – x3 – 8y3 = -16y3
Chọn đáp án B
Bài 5: Tìm x biết x2 – 16 + x(x – 4) = 0
A. x = 2 hoặc x = - 4.
B. x = 2 hoặc x = 4.
C. x = -2 hoặc x = - 4.
D. x = -2 hoặc x = 4.
Đáp án
Ta có: x2 – 16 + x(x – 4) = 0
⇔ (x + 4). (x - 4) + x.(x – 4) = 0
⇔ (x + 4 + x).(x - 4) = 0
⇔ (2x + 4). (x - 4) = 0
⇔ 2x + 4 = 0 hoặc x – 4 = 0
* Nếu 2x + 4 = 0 thì x = -2
* Nếu x – 4 =0 thì x = 4
Vậy x = -2 hoặc x = 4.
Chọn đáp án D
Bài 6: Rút gọn biểu thức A = (x + 2y ).(x - 2y) - (x – 2y)2
A. 2x2 + 4xy B. – 8y2 + 4xy
C. - 8y2 D. – 6y2 + 2xy
Đáp án
Ta có: A = (x + 2y ). (x - 2y) - (x – 2y)2
A = x2 – (2y)2 – [x2 – 2.x.2y +(2y)2 ]
A = x2 – 4y2 – x2 + 4xy - 4y22
A = -8y2 + 4xy
Chọn đáp án B
Bài 7: Điền vào chỗ trống: A = ( 1/2x - y )2 = 1/4x2 - ... + y2
A. 2xy B. xy
C. - 2xy D. 1/2 xy
Đáp ánÁp dụng hằng đẳng thức (a - b)2 = a2 - 2ab + b2.
Khi đó ta có A = ( 1/2x - y )2 = 1/4x2 - 2.1/2x.y + y2 = 1/4x2 - xy + y2.
Suy ra chỗ trống cần điền là xy.
Chọn đáp án B.
Bài 8: Điều vào chỗ trống: ... = ( 2x - 1 )( 4x2 + 2x + 1 ).
A. 1 - 8x3.
B. 1 - 4x3.
C. x3 - 8.
D. 8x3 - 1.
Đáp ánÁp dụng hằng đẳng thức a3 - b3 = ( a - b )( a2 + ab + b2 )
Khi đó ta có ( 2x - 1 )( 4x2 + 2x + 1 ) = ( 2x - 1 )[ ( 2x )2 + 2x.1 + 1 ] = ( 2x )3 - 1 = 8x3 - 1.
Suy ra chỗ trống cần điền là 8x3 - 1.
Chọn đáp án D.
Bài 9: Tính giá trị cuả biểu thức A = 8x3 + 12x2y + 6xy2 + y3 tại x = 2 và y = -1.
A. 1 B. 8
C. 27 D. -1
Đáp ánÁp dụng hằng đẳng thức ( a + b )3 = a3 + 3a2b + 3ab2 + b3.
Khi đó ta có:
A = 8x3 + 12x2y + 6xy2 + y3 = ( 2x )3 + 3.( 2x )2.y + 3.( 2x ).y2 + y3 = ( 2x + y )3
Với x = 2 và y = -1 ta có A = ( 2.2 - 1 )3 = 33 = 27.
Chọn đáp án C.
Bài 10: Tính giá trị của biểu thức A = 352 - 700 + 102.
A. 252. B. 152.
C. 452. D. 202.
Đáp ánTa có A = 352 - 700 + 102 = 352 - 2.35.10 + 102
Áp dụng hằng đẳng thức ( a - b )2 = a2 - 2ab + b2.
Khi đó A = ( 35 - 10 )2 = 252.
Chọn đáp án A.
Bài viết liên quan
- Toán lớp 8 Bài 2: Nhân đa thức với đa thức
- Toán lớp 8 Bài 3: Những hằng đẳng thức đáng nhớ
- Toán lớp 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp)
- Toán lớp 8 Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Toán lớp 8 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
