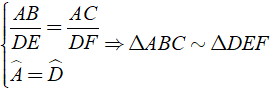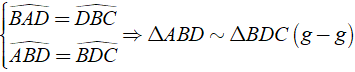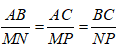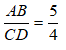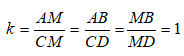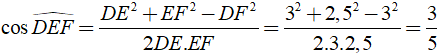Toán lớp 8 Bài 61: Trường hợp đồng dạng thứ hai
Lý thuyết tổng hợp Toán học lớp 8 Bài 61: Trường hợp đồng dạng thứ hai chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 61: Trường hợp đồng dạng thứ hai
A. Lý thuyết
a) Định nghĩa
Tổng quát: Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC ⇒ Δ ABC ∼ Δ A'B'C'
b) Ví dụ áp dụng
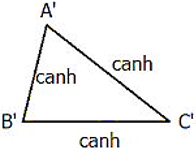
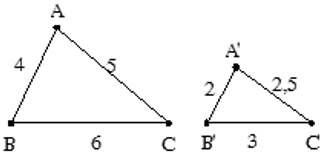
Ví dụ: Cho Δ ABC,Δ A'B'C' có độ dài các cạnh như hình vẽ. Chứng minh Δ ABC ∼ Δ A'B'C'
Hướng dẫn:
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )

B. Bài tập trắc nghiệm
Bài 1: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Đáp án
Ta có:
Chọn đáp án C.
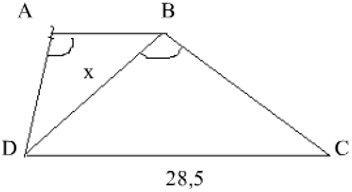
Bài 2: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
Đáp án
Xét Δ ABD và Δ BDC có:
⇒ AB/BD = AD/BC = BD/DC
hay 12,5/x = x/28,5 ⇒ x2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.
Bài 3: Cho tam giác ABC có M và N lần lượt là trung điểm của AC và AB. Gọi AD là tia phân giác của góc BACˆ = DBCˆ, tia AD cắt MN tại P. Hỏi tam giác nào đồng dạng với tam giác ANP
A. Δ ABD B. ΔAMP
C. ΔABD D. Δ ACD
Đáp án
Xét tam giác ABC có M và N lần lượt là trung điểm của AC và AB nên MN là đường trung bình của tam giác ABC
Suy ra: MN // BC
Xét tam giác ABD có MP// BD (vì MN// BC)
Suy ra: Tam giác ANP đồng dạng với tam giác ABD.
Chọn đáp án A
Bài 4: Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, gọi F là giao điểm của DE và BC. Tìm khẳng định sai
A. Δ DAE đồng dạng Δ FBE
B. Δ DAE đồng dạng ΔFCD
C. Δ DEA đồng dạng ΔFCD
D. Δ FBE đồng dạng ΔFCD
Đáp án
* Xét tam giác DAE và ΔFBE có:
∠AED = ∠BEF (2 góc đối đỉnh)
∠ADE = ∠EFB (2 góc so le trong )
Suy ra: Δ DAE đồng dạng Δ FBE ( g.g) (1)
* Vì ABCD là hình bình hành nên: BE// CD
Suy ra: Δ FBE đồng dạng ΔFCD ( định lí) (2)
Từ (1) và (2) suy ra Δ DAE đồng dạng ΔFCD ( bắc cầu)
Chọn đáp án C
Bài 5: Cho tam giác ABC có AB = 3cm, AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; NP = 10cm . Tìm khẳng định sai?
A. Tam giác ABC là tam giác nhọn
B. Δ ABC đồng dạng tam giác MNP
C. Tam giác ABC vuông tại A.
D. MP = 8cm
Đáp án
* Ta có: AB2 + AC2 = BC2 (32 + 42 = 52 = 25 )
Suy ra: tam giác ABC vuông tại A.
* Áp dụng định lí Py ta go vào tam giác MNP ta có:
NP2 = MN2 + MP2
Suy ra: MP2 = NP2 – MN2 = 102 – 62 = 64
Do đó MP = 8cm.
*Ta có:
Do đó, Δ ABC đồng dạng tam giác MNP (c.c.c)
Chọn đáp án A
Bài 6: Cho tam giác ABC có M, N và P lần lượt là trung điểm của AB ; AC; BC. Tìm khẳng định sai
A. ΔAMN đồng dạng ΔABC ( định lí)
B. ΔCNP đồng dạng ΔCAB ( định lí)
C. ΔAMN đồng dạng ΔNPC
D. Chỉ có đúng 2 cặp tam giác đồng dạng .
Đáp án
* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra : MN// BC
Tương tự có NP // AB
* Xét Δ AMN và ΔNPC có:
∠MAN = ∠PNC ( hai góc đồng vị )
∠ANM = ∠NCP ( hai góc đồng vị)
Suy ra: Δ AMN đồng dạng ΔNPC (g.g)
* Vì MN// BC nên ΔAMN đồng dạng ΔABC ( định lí)
* Vì NP // AB nên Δ CNP đồng dạng Δ CAB ( định lí)
Chọn đáp án D
Bài 7: Cho tam giác ABC có M là trung điểm của AC. Lấy điểm D đối xứng với B qua M . Khi đó :
A. Tứ giác ABCD là hình thoi
B. AC = BD
C. ΔAMB = ΔCMD theo tỉ số đồng dạng k = 1
D.
Đáp án
Xét Δ AMB và ΔCMD có:
AM = MC ( vì M là trung điểm của AC)
∠AMB = ∠CMD = 90o
BM = MD ( vì D đối xứng với B qua M)
Suy ra: Δ AMB = ΔCMD ( c.g.c)
Suy ra: Hai tam giác này cũng đồng dạng với nhau và tỉ số đồng dạng là:
D.
Chọn đáp án C
Bài 8: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Đáp ánÁp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta được
BC2 = AC2 + AB2 ⇒ AB = √ (BC2 - AC2) = √ (52 - 32) = 4( cm )
Ta có: cos ACBˆ = AC/BC = 3/5
Xét tam giác DEF có:
Khi đó ACBˆ = DEFˆ
Chọn đáp án B.
Bài 9: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Đáp ánTa có: RS/PQ = RK/PM = SK/QM ⇒ Δ RSK ∼ Δ PQM
Chọn đáp án A.
Bài 10: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Đáp ánTa có Δ RSK ∼ Δ PQM ⇔
Chọn đáp án A.