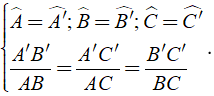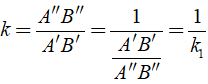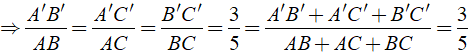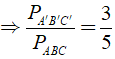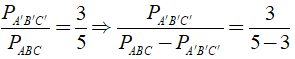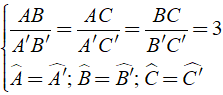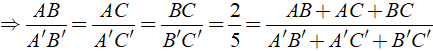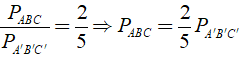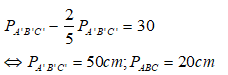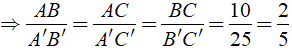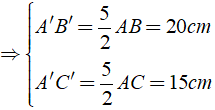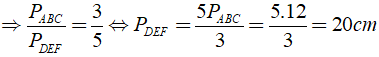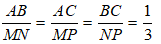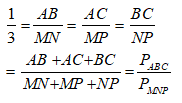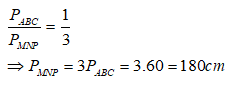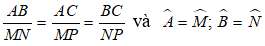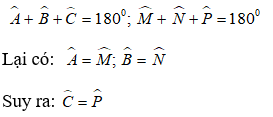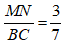Bài 59: Khái niệm hai tam giác đồng dạng

A. Lý thuyết

1. Tam giác đồng dạng

Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.

Tam giác ABC gọi là đồng dạng với tam giác A'B'C' nếu

Kí hiệu: Δ ABC ∼ Δ A'B'C'

Tỉ số cách cạnh tương ứng A'B'/AB = A'C'/AC = B'C'/BC = k được gọi là tỉ số đồng dạng

b) Tính chất

Hai tam giác A'B'C' và ABC đồng dạng có một số tính chất:

+ Δ ABC ∼ Δ A'B'C'

+ Nếu Δ ABC ∼ Δ A'B'C' thì Δ A'B'C' ∼ Δ ABC.

+ Nếu Δ A'B'C' ∼ Δ A''B''C'' và Δ A''B''C'' ∼ Δ ABC thì Δ ABC ∼ Δ A'B'C'

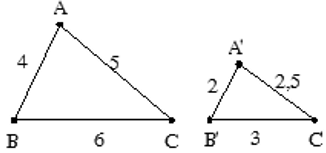
Ví dụ: Cho Δ ABC ∼ Δ A'B'C' như hình vẽ. Tính tỉ số đồng dạng ?

Hướng dẫn:

Ta có Δ ABC ∼ Δ A'B'C'. Khi đó tỉ số đồng dạng là

A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.

2. Định lý

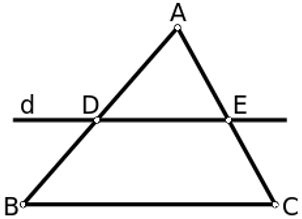
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

Tổng quát: Δ ABC,DE//BC ( D ∈ AB; E ∈ AC ).

Ta có: Δ ADE ∼ Δ ABC

Chú ý: Định lí cũng đúng cho trường hợp đường thẳng d cắt phần kéo dài của hai tam giác song song với cạnh còn lại.

3. Bài tập tự luyện

Hướng dẫn:

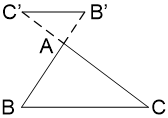
Gọi tỉ số đồng dạng của Δ A''B''C'' ∼ Δ A'B'C' là k

Ta có:

Điều đó chứng tỏ Δ A''B''C'' ∼ Δ A'B'C' theo tỉ số đồng dạng là k = 1/k₁

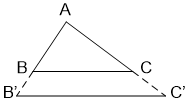
Gọi tỉ số đồng dạng của Δ A'B'C' ∼ Δ ABC là k₃

Thì k₁ = A'B'/A''B'', k₂ = A''B''/AB ⇒ k₃ = A'B'/AB = A'B'/A''B''.A''B''/AB = k₁.k₂

Điều đó chứng tỏ Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k₃ = k₁k₂

Bài 2: Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5

a) Tính tỉ số chu vi của hai tam giác đã cho.

b) Cho biết hiệu chu vi của hai tam giác trên là 40dm. Tính chu vi của hai tam giác đã cho

Hướng dẫn:

a) Ta có: Δ A'B'C' ∼ Δ ABC

b) Theo giả thiết ta có: P_ABC - P_A'B'C' = 40dm

Khi đó ta có: 

hay P_A'B'C'/40 = 3/2 ⇒ P_A'B'C' = 60( dm ); P_ABC = 20dm.

B. Bài tập về nhà

Bài 1: Ta có Δ MNP ∼ Δ ABC thì

   A. MN/AB = MP/AC

   B. MN/AB = MP/BC

   C. MN/AB = NP/AC

   D. MN/BC = NP/AC

Bài 2: Cho Δ ABC ∼ Δ A'B'C' có AB = 3A'B'. Kết quả nào sau đây sai?

   A. Aˆ = A'ˆ; Bˆ = B'ˆ

   B. A'C' = 1/3AC

   C. AC/BC = A'C'/B'C' = 3

   D. AB/A'B' = AC/A'C' = BC/B'C'

Bài 3: Cho Δ ABC ∼ Δ A'B'C' có AB/A'B' = 2/5. Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng?

   A. Chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.

   B. Chu vi của Δ ABC là 50cm, chu vi của Δ A'B'C' là 20cm.

   C. Chu vi của Δ ABC là 45cm, chu vi của Δ A'B'C' là 75cm.

   D. Cả 3 đáp án đều sai.

Bài 4: Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C'

   A. 4cm; 3cm   B. 7,5cm; 10cm

   C. 4,5cm; 6cm   D. 15cm; 20cm

Bài 5: Cho Δ ABC ∼ Δ DEF có tỉ số đồng dạng là k = 3/5, chu vi của Δ ABC bằng 12cm. Chu vi của Δ DEF là?

   A. 7,2cm   B. 20cm

   C. 3cm   D. 17/3cm

Bài 6: Cho hai tam giác ABC và MNP đồng dạng với nhau. Biết

 và chu vi tam giác ABC là 60cm . Tính chu vi tam giác MNP?

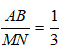
   A. 180cm     B. 20cm

   C. 30cm     D. 57cm

Bài 7: Cho hai tam giác ABC và MNP có:

Tìm khẳng định đúng

   A. Hai tam giác ABC và MNP đồng dạng với nhau.

   B. Chưa thể kết luận hai tam giác này đồng dạng.

   C. ∠C ≠ ∠P

   D. Tất cả sai.

Bài 8: Cho tam giác ABC, gọi M, N và P theo thứ tự là trung điểm của AB, AC và BC. Khi đó tam giác AMN đồng dạng với tam giác nào ?

   A. ΔAMC     B. ΔABC

   C. ΔABP     D. ΔAPC

Bài 9: Cho tam giác ABC, trên đoạn thẳng AB và AC lấy các điểm M và N sao cho AM = 6cm; MB = 8cm; AN = 3cm và AC = 7cm. Tìm khẳng định sai ?

   A. 

   B. Hai tam giác AMN và ABC đồng dạng với nhau

   C. MN// BC

   D. Tam giác AMC đồng dạng với tam giác ABN.

Ta có: NC = AC – AN = 7 – 3 = 4cm

Vì

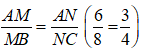
nên MN // BC (định lí Ta let đảo)

Suy ra: Tam giác AMN đồng dạng với tam giác ABC.

Ta có:

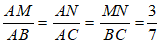
Chọn đáp án D

Bài 10: Cho 2 tam giác ABC và MNP đồng dạng với nhau. Biết chu vi tam giác ABC là 40cm; AB = 4cm; MN = 10cm . Tính chu vi tam giác MNP?

   A. 50cm     B. 60cm

   C. 100cm     D. 80cm

Vì tam giác ABC đồng dạng với tam giác MNP nên;

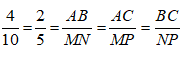
Theo tính chất dãy tỉ số bằng nhau ta có:

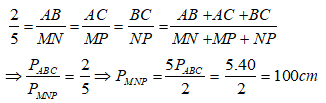
Chọn đáp án C