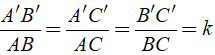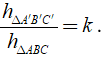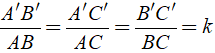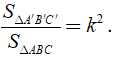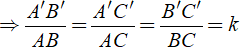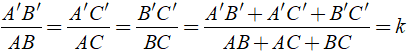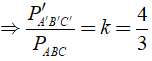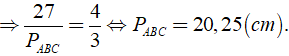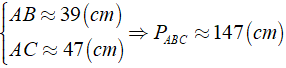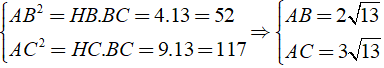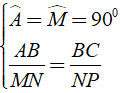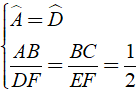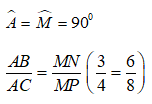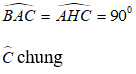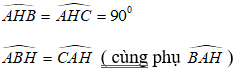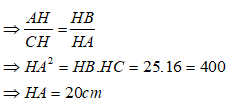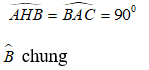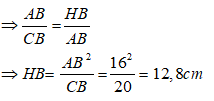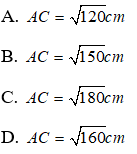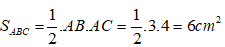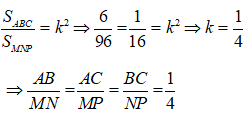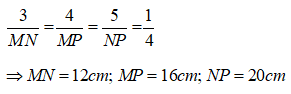Bài 63: Các trường hợp đồng dạng của tam giác vuông

A. Lý thuyết

1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông

Hai tam giác vuông đồng dạng với nhau nếu:

+ Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.

+ Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.

2. Dấu hiệu đặc biệt nhận biết hai tam vuông đồng dạng

Định lý 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

Tổng quát: Δ ABC,Δ A'B'C', Aˆ = A'ˆ = 90⁰; B'C'/BC = A'B'/AB

\Rightarrow Δ ABC ∈ Δ A'B'C'.

3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng

Định lý 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.

Tổng quát: Ta có tỉ số đồng dạng là

Tỉ số hai đường cao là :

Định lý 3: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

Tổng quát: Ta có tỉ số đồng dạng là

Tỉ số diện tích hai tam giác đồng dạng là :

4. Mở rộng

Nếu hai tam giác đồng dạng với nhau thì:

+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

+ Tỉ số các chu vi bằng tỉ số đồng dạng.

+ Tỉ số các diện tích bằng bình phương tỉ số đồng dạng.

5. Ví dụ áp dụng

Ví dụ: Cho tam giác đồng dạng với tam giác ABC theo tỉ số k = 4/3. Tính chu vi của tam giác ABC, biết chu vi của tam giác A'B'C' bằng 27cm.

Hướng dẫn:

Ta có Δ A'B'C' ∈ Δ ABC theo tỉ số k

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

6. Bài tập tự luyện

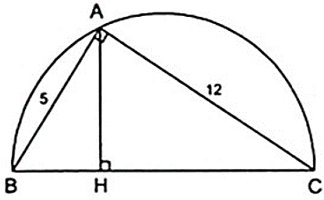
Bài 1: Cho hình bên là tam giác ABC vuông tại A, đường cao AH

a) Trong hình bên có bao nhiêu cặp tam giác đồng dạng với nhau. Hãy chỉ ra các cặp đồng dạng và theo các đỉnh tương ứng.

b) Cho biết AB = 5cm, AC = 12cm. Tinh độ dài các đoạn thẳng BC, AH, BH và CH.

Hướng dẫn:

a) Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.

b) Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta có:

BC² = CA² + AB² ⇒ BC² = 12² + 5² = 13² ⇔ BC = 13( cm )

Vì S_ABC = 1/2AB.AC = 1/2AH.BC ⇒ AH.BC = AB.AC

Hay 12.5 = AH.13 ⇒ AH = 60/13 ( cm )

Từ câu a ta có: Δ BHA ∼ Δ BAC ⇒ BH/BA = BA/BC hay BH/5 = 5/13 ⇔ BH = 25/13( cm )

Do đó: CH = BC - BH = 13 - 25/13 = 144/13( cm )

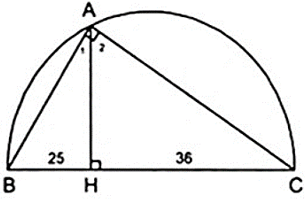
Bài 2: Chân đường cao AH chia cạnh huyền BC thành hai đoạn thẳng có độ dài lần lượt là 25 cm và 36 cm. Tính chu vi và diện tích của tam giác đó.

Hướng dẫn:

Ta có: Δ AHB ∼ Δ CHA ⇒ AH/HC = HB/HA

Hay HA/36 = 25/HA ⇔ HA² = 30² ⇒ HA = 30( cm )

Ta có: S_ABC = 1/2AH.BC = 1/2.30.61 = 915( cm² )

Áp dụng định lý Py – ta –go ta được:

B. Bài tập trắc nghiệm

Bài 1: Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?

   A. S_ABC = 39cm²   B. S_ABC = 36cm²

   C. S_ABC = 78cm²   D. S_ABC = 18cm²

Bài 2: Cho Δ ABC và Δ MNP có Aˆ = Mˆ = 90⁰, AB/MN = BC/NP thì?

   A. Δ ABC ∼ Δ PMN

   B. Δ ABC ∼ Δ NMP

   C. Δ ABC ∼ Δ MNP

   D. Δ ABC ∼ Δ MPN

Bài 3: Nếu hai tam giác đồng dạng với nhau thì: Chọn phát biểu sai trong các phát biểu sau?

   A. Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

   B. Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

   C. Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

   D. Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng.

Bài 4: Cho hai tam giác ABC và DEF có Aˆ = Dˆ = 90⁰ ,AB = 3cm, BC = 5cm,EF = 10cm, DF = 6cm. Chọn phát biểu đúng trong các phát biểu sau?

   A. Δ ABC ∼ Δ DEF   B. Δ ABC ∼ Δ EDF

   C. Δ ABC ∼ Δ DFE   D. Δ ABC ∼ Δ FDE

Bài 5: Cho tam giác ABC có AB = 3cm; AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; MP = 8cm. Tìm khẳng định sai

   A. Tam giác ABC là tam giác vuông

   B. Δ ABC và ΔMNP đồng dạng với nhau

   C. NP = 10 cm

   D. Có hai phương án sai

Bài 6: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Tìm tam giác đồng dạng với tam giác ABC?

   A. ΔHAC     B. ΔAHC

   C. ΔAHB     D. ΔABH

Bài 7: Cho ta giác ABC vuông tại A, kẻ AH vuông góc BC. Biết BH = 25 và HC = 36. Tính AH?

   A. 18cm     B. 25cm

   C. 20cm     D. 32cm

Bài 8: Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. Biết BC = 20cm, AC = 12cm. Tính BH?

   A. 12cm     B. 12,5cm

   C. 15cm     D. 12,8cm

Bài 9: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 6cm, BH = 3cm. Tính AC?

Bài 10: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm . Tam giác MNP đồng dạng với tam giác ABC và diện tích tam giác MNP là 96cm². Tính độ dài các cạnh của tam giác MNP?

   A. 9cm, 12cm, 15cm

   B. 12cm, 16cm ; 20cm

   C. 6cm, 8cm, 10cm

   D. Đáp án khác