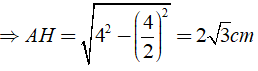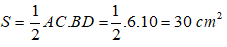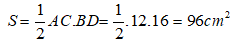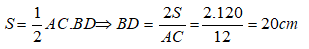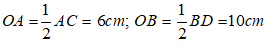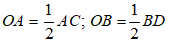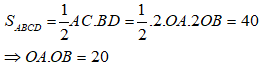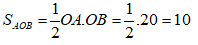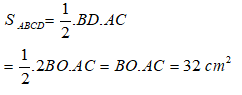Toán lớp 8 Bài 41: Diện tích hình thoi
Lý thuyết tổng hợp Toán học lớp 8 Bài 41: Diện tích hình thoi chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 41: Diện tích hình thoi
A. Lý thuyết
1. Công thức tính diện tích hình thoi
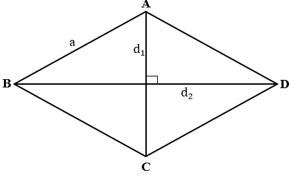
Diện tích hình thoi bằng nửa tích hai đường chéo.
Ta có: S = 1/2d1.d2
Ví dụ: Cho hình thoi có lần lượt độ dài hai đường chéo là 10cm, 15cm. Tính diện tích hình thoi đó ?
Hướng dẫn:
Diện tích hình thoi là : S = 1/2.10.15 = 75( cm2 ).

2. Bài tập tự luyện
Bài 1: Cho hình thoi ABCD có AB = 13cm, AC = 10cm. Tính diện tích của hình thoi ?
Hướng dẫn:
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HA = HC = 5( cm )
Áp dụng định lí Py – to – go ta có:
AB2 = AH2 + HB2 ⇒ BH = √ (AB2 - AH2)
⇒ HB = √ (132 - 52) = 12( cm )
⇒ BD = HB + HD = 2HB = 2.12 = 24( cm )
Khi đó ta có SABCD = 1/2AC.BD = 1/2.10.24 = 120( cm2 ).
Vậy diện tích của hình thoi là 120( cm2 )
Bài 2: Tính diện tích hình thoi có cạnh là 17cm và tổng hai đường chéo là 46cm.
Hướng dẫn:
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46( cm )
⇔ ( HB + HD ) + ( HC + HA ) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có: HA + HB = 23 ⇔ ( HA + HB )2 = 232
⇔ HA2 + 2HA.HB + HB2 = 232 ( 1 )
Mặt khác, theo định lí Py – to – go ta có: AH2 + HB2 = AB2 = 172 ( 2 )
Từ ( 1 ) và ( 2 ) ta có: 172 + 2HA.HB = 232 ⇒ HA.HB = (232 - 172)/2 = 120.
Hay AC/2.BD/2 = 120 ⇔ 1/2.AC.BD = 240 ⇒ SABCD = 240( cm2 )
Vậy diện tích hình thoi là 240cm2.
B. Bài tập trắc nghiệm
Bài 1: Cho hình thoi có độ dài hai đường chéo lần lượt là 8cm, 10cm. Diện tích hình thoi là?
A. 80cm2. B. 40cm2.
C. 18cm2. D. 9cm2.
Đáp ánDiện tích của hình thoi là S = 1/2d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = 1/2.8.10 = 40( cm2 )
Chọn đáp án B.
Bài 2: Hình thoi có độ dài hai đường chéo lần lượt là a√ 2 ,cm, a√ 3 cm. Diện tích của hình thoi là ?
A. a2√ 6 ( cm2 )
B. (a2√ 6 )/3( cm2 )
C. (a2√ 6 )/2( cm2 )
D. (a2√ 5 )/2( cm2 )
Đáp ánDiện tích của hình thoi là S = 1/2d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = 1/2. a√ 2 . a√ 3 = (a2√ 6 )/2( cm2 )
Chọn đáp án C.
Bài 3: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và BACˆ = 600. Diện tích của hình thoi ABCD là ?
A. 8( cm2 ) B. 8√ 3 ( cm2 )
C. 16( cm2 ) D. 16√ 3 ( cm2 )
Đáp ánXét hình thoi ABCD có BACˆ = 600.
Ta có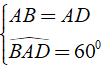
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – to – go ta có:
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2)
⇒ AC = 2AH = 4√ 3 ( cm )
Do đó SABCD = 1/2AC.BD = 1/2.4√ 3 .4 = 8√ 3 ( cm2 )
Chọn đáp án B.
Bài 4: Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là ?
A. 16( cm2 )
B. 8√ 21 ( cm2 )
C. 16√ 21 ( cm2 )
D. 8( cm2 )
Đáp ánGọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2) = √ (102 - 42) = 2√ 21 ( cm )
⇒ AC = 2AH = 4√ 21 ( cm )
Do đó SABCD = 1/2.BD.AC = 1/2.4√ (21) .8 = 16√ 21 ( cm2 )
Chọn đáp án C.
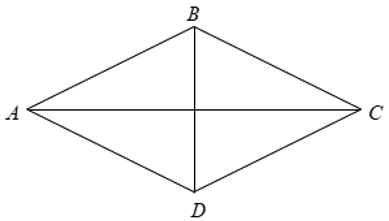
Bài 5: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Biết OA = 3cm và OB = 5cm. Tính diện tích hình thoi?
A. 30cm2 B. 35cm2
C. 40cm2 D. 45cm2
Đáp ánVÌ ABCD là hình thoi nên O là trung điểm của AC và BD
Suy ra: AC = 2OA = 2.3 = 6cm
Và BD = 2.OB = 2.5= 10cm
Diện tích hình thoi là:
Chọn đáp án A
Bài 6: Cho hình bình hành ABCD có AB = BC = 10 cm và O là giao điểm của hai đường chéo sao cho OA = 6cm. Tính diện tích hình bình hành ABCD
A. 96 B. 80
C. 72 D. 64
Đáp ánVì hình bình hành ABCD có 2 cạnh liền kề bằng nhau AB = BC nên ABCD là hình thoi
Suy ra: AB = BC = CD= DA = 10cm và O là trung điểm của AC và trung điểm của BD
Ta có: AC = 2AO = 2. 6 = 12cm
Áp dụng định lí py tago vào tam giác AOD có:
AD2 = AO2 + OD2 suy ra: OD2 = AD2 – AO2 = 102 – 62 = 64 nên OD = 8cm
Suy ra: BD = 2OD = 16cm
Diện tích hình thoi ABCD là:
Chọn đáp án A
Bài 7: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Diện tích của hình thoi là 120cm2; AC = 12cm . Tính độ dài cạnh của hình thoi
A. 2√30cm B. 2√34cm
C. 8cm D. 9cm
Đáp ánDiện tích của hình thoi là:
Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD.
Suy ra:
Áp dụng định lí Pytago vào tam giác OAB có:
AB2 = OA2 + OB2 = 62 + 102 = 136
⇒ AB = 2√34cm
Chọn đáp án B
Bài 8: Cho hình thoi ABCD có diện tích là 24cm2. Tỉ số độ dài hai đường chéo là 3: 4. Tính độ dài hai đường chéo của hình thoi
A. 9cm và 12cm B. 12cm và 16cm
C. 6cm và 8cm D. 3cm và 4cm
Đáp ánChọn đáp án C
Bài 9: Cho hình thoi ABCD có diện tích là 40cm2. Gọi O là giao điểm của hai đường chéo.. Tính diện tích tam giác AOB?
A. 10 cm2 B. 12 cm2
C. 8 cm2 D. 5 cm2
Đáp ánVì ABCD là hình thoi có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD.
Suy ra
Diện tích hình thoi ABCD là:
Diện tích tam giác vuông OAB là:
Chọn đáp án A
Bài 10: Cho hình thoi ABCD có O là giao điểm của hai đường chéo biết diện tích tam giác ABC là 16cm2. Tính diện tích hình thoi ABCD?
A. 24cm2 B. 32cm2
C. 48cm2 D. 64cm2
Đáp ánDo ABCD là hình thoi nên hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
Diện tích tam giác ABC là
Suy ra: BO.AC = 32
Diện tích hình thoi ABCD là:
Chọn đáp án B