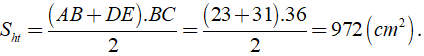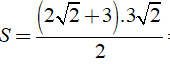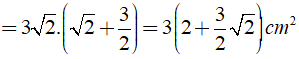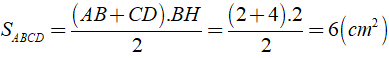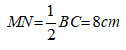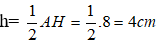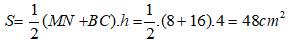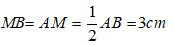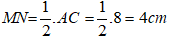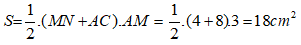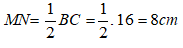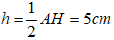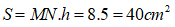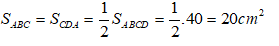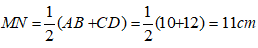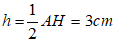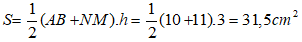Toán lớp 8 Bài 40: Diện tích hình thang
Lý thuyết tổng hợp Toán học lớp 8 Bài 40: Diện tích hình thang chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 40: Diện tích hình thang
A. Lý thuyết
1. Công thức diện tích của hình thang
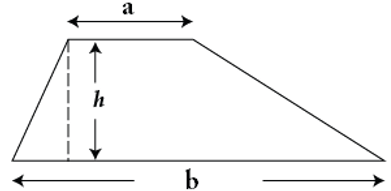
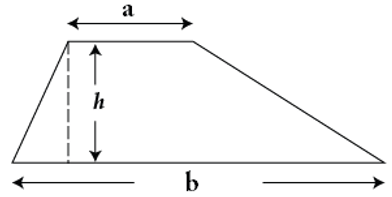
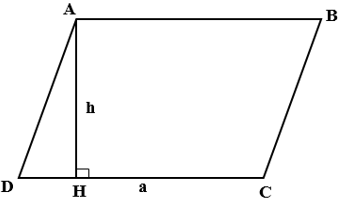
Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
Ta có: S = 1/2( a + b ).h
Lý thuyết tính diện tích hình thang: Muốn tính diện tích hình thang ta cộng tổng hai đáy rồi nhân với chiều cao, sau đó chia đôi.
Ví dụ: Cho hình thang ABCD ( AB//CD ) có AB = 3cm; CD = 5cm, chiều cao hình thang là h = 4cm. Tính diện tích hình thang ?
Hướng dẫn:
Diện tích hình thang cần tìm là SABCD = 1/2( AB + CD ).h = 1/2( 3 + 5 ).4 = 16( cm2 )
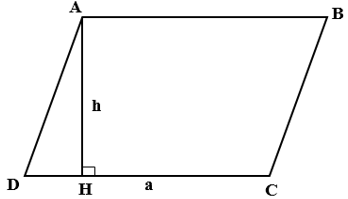
2. Công thức tính diện tích hình bình hành
Ta có : S = a.h
Ví dụ: Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 5cm, độ dài đường cao hình bình hành là h = 4cm. Tính diện tích của hình bình hành?
Diện tích hình hình hành là SABCD = AB.h = 4.5 = 20( cm2 )
3. Bài tập tự luyện
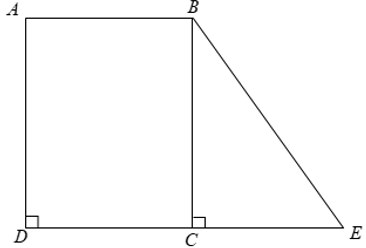
Bài 1: Tính diện tích mảnh đất hình thang ABED có AB = 23cm, DE = 31cm và diện tích hình chữ nhật ABCD là 828cm2.
Hướng dẫn:
Theo bài ra ta có SABCD = AB.BC = 23.BC = 828 ⇒ BC = 36 ( cm )
Khi đó ta có
Vậy diện tích hình thang ABED là 972( cm2 )
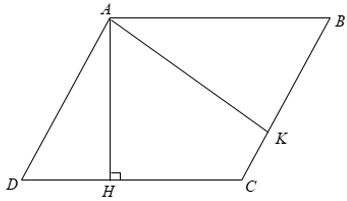
Bài 2: Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp án ?
Hướng dẫn:
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
+ Shbh = AH.CD = 8.AH
+ Shbh = AK.BC = 6.AK
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = (8.5)/6 = 20/3( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = (6.5)/8 = 15/4( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số
B. Bài tập trắc nghiệm
Bài 1: Hình thang có độ dài đáy lần lượt là 2√ 2 cm, 3cm và chiều cao là 3√ 2 cm. Diện tích của hình thang là ?
A. 2( 2 + √ 2 )cm2.
B. 3( 2 + 3/2√ 2 )cm2.
C. 3( 3 + √ 2 )cm2.
D. 3( 2 + √ 2 /2 )cm2
Đáp ánTa có: S = 1/2( a + b ).h
Khi đó ta có:
Chọn đáp án B.
Bài 2: Hình thang có độ dài đáy lần lượt là 6cm, 4cm và diện tích hình thang đó là 15cm2. Chiều cao hình thang có độ dài là ?
A. 3cm. B. 1,5cm
C. 2cm D. 1cm
Đáp ánDiện tích của hình thang là S = 1/2( a + b ).h
⇒ ( a + b ).h = 2S ⇔ h = (2S)/(a + b).
Khi đó, chiều cao của hình thang là h = (2.15)/(6 + 4) = 3( cm ).
Chọn đáp án A.
Bài 3: Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 4cm, độ dài đường cao hình bình hành là h = 2cm. Diện tích của hình bình hành là?
A. 4( cm2 ) B. 8( cm2 )
C. 6( cm2 ) D. 3( cm2 )
Đáp ánTa có : S = a.h
Khi đó ta có: S = 4.2 = 8( cm2 ).
Chọn đáp án B.
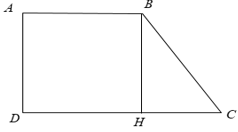
Bài 4: Cho hình thang vuông ABCD ( Aˆ = Dˆ = 900 ), trong đó có Cˆ = 450, AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3( cm2 ) B. 8( cm2 )
C. 4( cm2 ) D. 6( cm2 )
Đáp ánXét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.
Mà BCDˆ = 450 ⇒ BDCˆ = 450
⇒ DBCˆ = 1800 - ( BCDˆ + BDCˆ ) = 1800 - 900 = 900.
⇒ Δ BDC là tam giác vuông cân tại B nên BH = 1/2DC = 2cm.
Do đó
Chọn đáp án D.
Bài 5: Cho tam giác ABC có BC = 16cm ,đường cao AH = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính diện tích của tứ giác MNCB?
A. 48cm2 B. 40cm2
C. 54cm2 D. 60cm2
Đáp ánXét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.
Suy ra: MN // BC và
Do đó, tứ giác MNCB là hình thang .
Vì AH = 8cm nên đường cao kẻ từ M đến BC bằng
Diện tích hình thang MNCB là :
Chọn đáp án A
Bài 6: Cho tam giác ABC vuông tại A có AB = 6cm và BC = 10cm . Gọi M và N theo thứ tự là trung điểm của AB và BC. Tính diện tích của tứ giác MNCA?
A. 10 cm2 B. 12cm2
C. 15cm2 D. 18cm2
Đáp ánVì M là trung điểm của AB nên:
Áp dụng định lí py tago vào tam giác ABC có:
BC2 = AB2 + AC2 suy ra: AC2 = BC2 - AB2 = 102 - 62 = 64
Suy ra: AC = 8cm
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC nên: MN// AC và
Suy ra: tứ giác MNCA là hình thang vuông.
Diện tích hình thang MNCA là:
Chọn đáp án
Bài 7: Cho tam giác ABC có M, N và P lần lượt là trung điểm của AB, AC và P. Biết đường cao AH = 10cm và BC = 16cm . Tính diện tích tứ giác MNPB?
A. 20cm2 B. 30cm2
C. 40cm2 D. 50cm2
Đáp ánXét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra: MN// BC và
Tương tự, có NP là đường trung bình của tam giác nên: NP // AB
Xét tứ giác MNPB có MN// BC và NP // AB
Suy ra: tứ giác MNPB là bình hành.
Tam giác ABC có đường cao AH = 10cm nên đường cao ứng với cạnh đáy của hình bình hành MNPB là:
Diện tích hình bình hành MNPB là:
Chọn đáp án C
Bài 8: Cho hình bình hành ABCD có diện tích là 40cm2. Tính diện tích tam giác ABC?
A. 10cm2 B. 15cm2
C. 20cm2 D. 18cm2
Đáp ánDo ABCD là hình bình hành nên: AB = CD và BC = AD
Xét tam giác ABC và tam giác CDA có :
AB = CD
BC = AD
AC chung
⇒ ΔABC = ΔCDA (c.c.c)
Suy ra: SABC = SCDA
Mà SABC + SCDA = SABCD
Do đó
Chọn đáp án C
Bài 9: Cho hình thang ABCD (AB// CD) có AB = 6cm và CD = 10cm. Biết diện tích hình thang ABCD là 60cm2. Tính diện tích tam giác ACD?
A. 37,5cm2 B. 35cm2
C. 30cm2 D. 40cm2
Đáp ánChọn đáp án A
Bài 10: Cho hình thang ABCD có AB// CD; AB = 10cm , CD = 12cm, đường cao AH = 6cm . Gọi M và N lần lượt là trung điểm của AD và BC. Tính diện tích tứ giác ABNM?
A. 30cm2 B. 29,5cm2
C. 27,5cm2 D.31,5cm2
Đáp ánXét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang:
Suy ra: MN// AB// CD và
Suy ra: tứ giác MNCD là hình thang.
Vì M là trung điểm của AD và đường cao AH = 6cm nên chiều cao xuất phát từA của hình thang MNCD là:
Diện tích hình thang ABNM là :
Chọn đáp án D