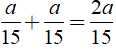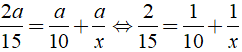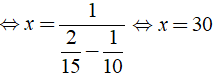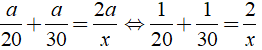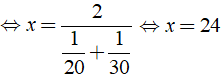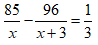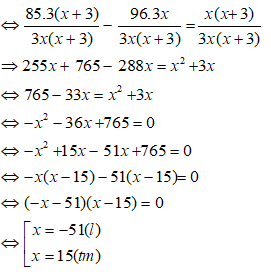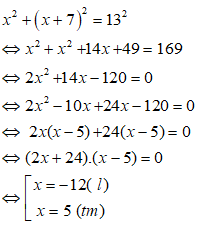Toán lớp 8 Bài 48: Giải bài toán bằng cách lập phương trình
Lý thuyết tổng hợp Toán học lớp 8 Bài 48: Giải bài toán bằng cách lập phương trình chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 48: Giải bài toán bằng cách lập phương trình
A. Lý thuyết
1. Cách giải toán
Các bước giải toán bằng cách lập phương trình:
Bước 1: Lập phương trình
+ Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
+ Biểu diễn các đại lượng chưa biết khác theo ẩn và các đại lượng đã biết.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Trả lời
Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
2. Chú ý về chọn ẩn và điều kiện thích hợp của ẩn
Thông thường thì bài toán hỏi về đại lượng gì thì chọn ẩnlà đại lượng đó.
Về điều kiện thích hợp của ẩn
+ Nếu x biểu thị một chữ số thì 0 ≤ x ≤ 9, x ∈ N
+ Nếu x biểu thị tuổi, sản phẩm, người thì x nguyên dương.
+ Nếu x biểu thị vận tốc của chuyển động thì x > 0.
Hướng dẫn:
Gọi x là số nhỏ trong hai số nguyên cần tìm; x ∈ Z.
⇒ x + 1 là số thứ hai cần tìm.
Theo giả thiết, ta có 2 lần số nhỏ cộng 3 lần số lớn bằng - 87
Khi đó ta có: 2x + 3( x + 1 ) = - 87
⇔ 2x + 3x + 3 = - 87 ⇔ 5x = - 90 ⇔ x = - 18.
So sánh với điều kiện x = - 18 thỏa mãn.
Vậy: Số thứ nhất cần tìm là - 18, số thứ hai là - 17.
Ví dụ 2: Một đội công nhân sửa một đoạn đường trong 3 ngày. Ngày thứ nhất đội sửa được 1/3 đoạn đường, ngày thứ hai đội sửa được một đoạn đường bằng 4/3 đoạn được làm được trong ngày thứ nhất, ngày thứ ba đội sửa 80m còn lại. Tính chiều dài đoạn đường mà đội phải sửa.
Hướng dẫn:
Gọi x ( m ) là độ dài đoạn đường đội công nhân đó phải sửa; x > 80.
+ Ngày thứ nhất đội đó sửa được x/3 ( m ) đường.
+ Ngày thứ hai đội đó sửa được 4/3.x/3 = (4x)/9 ( m ) đường
+ Ngày thứ ba đội đó sửa được x - x/3 - (4x)/9 = (2x)/9 ( m )
Theo giả thiết ngày thứ ba đội đó sửa được 80m
Khi đó ta có (2x)/9 = 80 ⇔ x = 80:2/9 = 360 ( m ).
Vậy độ dài quãng đường cần sửa là 360 m.
Chú ý: Một số dạng toán thường gặp
Dạng 1: Loại tìm số gồm hai hoặc ba chữ số
Số có hai chữ số có dạng: xy− = 10x + y. Điều kiện: x,y ∈ N, 0 < x ≤ 9, 0 ≤ y ≤ 9.
Số có ba chữ số có dạng: xyz− = 100x + 10y + z. Điều kiện: x,y,z ∈ N, 0 < x ≤ 9, 0 ≤ y,z ≤ 9.
Dạng 2: Làm công việc chung – riêng .
Năng suất làm việc là phần việc làm được trong một đơn vị thời gian.
Gọi A là khối lượng công việc, n là năng suất, t là thời gian làm việc. Ta có: A = n.t.
Tổng năng suất riêng bằng năng suất chung khi cùng làm.
Dạng 3: Loại toán chuyển động
Gọi s là quãng đường động tử đi, v là vận tốc, t là thời gian đi, ta có: s = v.t.
Vận tốc xuôi dòng nước = Vận tốc lúc nước yên lặng + Vận tốc dòng nước
Vận tốc ngược dòng nước = Vận tốc lúc nước yên lặng – Vận tốc dòng nước
Dạng 4: Loại toán về hình hình học
Hình chữ nhật có hai kích thước a, b. Diện tích: S = a.b; Chu vi: P = 2( a + b )
Tam giác vuông có hai cạnh góc vuông a, b. Diện tích: S = 1/2ab.
Hướng dẫn:
Gọi t ( h ) là thời gian từ lúc xe hơi chạy đến lúc đuổi kịp xe đạp; t > 0.
⇒ t + 3 ( h ) là thời gian kể từ lúc xe đạp đi đến lúc xe hơi đuổi kịp.
+ Quãng đường xe đạp đi được là s1 = 20( t + 3 ) km.
+ Quãng đường xe hơi đi được là s2 = 50t km.
Vì hai xe xuất phát tại điểm A nên khi gặp nhau s1 = s2.
Khi đó ta có: 20( t + 3 ) = 50t ⇔ 50t - 20t = 60 ⇔ 30t = 60 ⇔ t = 2( h ) (thỏa mãn)
Vậy xe hơi chạy được 2 giờ thì đuổi kịp xe đạp.
Ví dụ 4: Chu vi một khu vườn hình chữ nhật bằng 60m, hiệu độ dài của chiều dài và chiều rộng là 20m. Tìm độ dài các cạnh của hình chữ nhật.
Hướng dẫn:
Gọi x ( m ) là độ dài chiều rộng của hình chữ nhật; x > 0.
⇒ x + 20 ( m ) là độ dài chiều dài của hình chữ nhật.
Theo giả thiết ta có chu vi hình chữ nhật bằng 60 m.
Khi đó ta có P = 2( x + x + 20 ) = 60 ⇔ 2x + 20 = 30 ⇔ 2x = 10 ⇔ x = 5.
Do đó: Chiều rộng hình chữ nhật là 5m.
Chiều dài hình chữ nhật là 25m.
3. Bài tập tự luyện
Bài 1: Hai lớp A và B của một trường trung học tổ chức cho học sinh tham gia một buổi meeting. Người ta xem xét số học sinh mà một học sinh lớp A nói chuyện với học sinh lớp B thì thấy rằng: Bạn Khiêm nói chuyện với 5 bạn, bạn Long nói chuyện với 6 bạn, bạn Tùng nói chuyện với 7 bạn,…và đến bạn Hải là nói chuyện với cả lớp B. Tính số học sinh lớp B biết 2 lớp có tổng cộng 80 học sinh.
Hướng dẫn:
Gọi số học sinh lớp A là x (x ∈ N*, x < 80)
Bạn thứ nhất của lớp A (Khiêm) nói chuyện với 4 + 1 bạn
Bạn thứ hai của lớp A (Long) nói chuyện với 4 + 2 bạn
…………………
Bạn thứ x của lớp A (Hải) nói chuyện với bạn
Do đó số học sinh lớp B là 4 + x
Vì 2 lớp có tổng cộng 80 học sinh nên ta có:
x + (4 + x) = 80
⇔ 2x - 76 = 0
⇔ x = 38
Vậy số học sinh lớp B là: 80 - 38 = 42 (Học sinh)
Bài 2: Khiêm đi từ nhà đến trường Khiêm thấy cứ 10 phút lại gặp một xe buýt đi theo hướng ngược lại. Biết rằng cứ 15 phút lại có 1 xe buýt đi từ nhà Khiêm đến trường là cũng 15 phút lại có 1 xe buýt đi theo chiều ngược lại. Các xe chuyển động với cùng vận tốc. Hỏi cứ sau bao nhiêu phút thì có 1 xe cùng chiều vượt qua Khiêm.
Hướng dẫn:
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là:
Ta có phương trình:
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.
B. Bài tập trắc nghiệm
Bài 1: Mẹ hơn con 24 tuổi. Sau 2 năm nữa thì tuổi mẹ gấp 3 lần tuổi con. Tuổi của con hiện nay là:
A. 5. B. 10.
C. 15. D. 20.
Đáp ánGọi số tuổi của con hiện tại là x (Tuổi) (x ∈ N)
→ số tuổi của mẹ là x + 24 (Tuổi)
Theo bài ra ta có: 3(x + 2) = x + 24 + 2
⇔ 3x + 6 = x + 26
⇔ 2x - 20 = 0
⇔ x = 10
Vậy hiện tại tuổi của con là 10 tuổi.
Chọn đáp án B.
Bài 2: Tìm hai số tự nhiên chẵn liên tiếp biết biết tích của chúng là 24 là:
A. 2;4 B. 4;6
C. 6;8 D. 8;10
Đáp ánGọi 2 số chẵn liên tiếp cần tìm là x; x + 2 (x chia hết 2; x ∈ N)
Theo bài ra ta có: x(x + 2) = 24 ⇔ x2 + 2x - 24 = 0
⇔ (x - 4)(x + 6) = 0 ⇔ x = 4 (Do x + 6 > 0 ∀ x ∈ N)
Vậy hai số cần tìm là 4; 6.
Bài 3: Một hình chữ nhật có chiều dài hơn chiều rộng 3cm. Chu vi hình chữ nhật là 100cm. Chiều rộng hình chữ nhật là:
C. 100cm D. 3cm
Đáp ánGọi chiều rộng hình chữ nhật là x(cm) (x > 0)
→ Chiều dài hình chữ nhật là x + 3(cm)
Do chu vi hình chữ nhật là 100cm nên ta có:
2[ x + (x + 3) ] = 100 ⇔ 2x + 3 = 50 ⇔ x = 23,5
Vậy chiều rộng hình chữ nhật là 23,5cm
Chọn đáp án A.
Bài 4: Một xe đạp khởi hành từ điểm A, chạy với vận tốc 15 km/h. Sau đó 6 giờ, một xe hơi đuổi theo với vận tốc 60 km/h. Hỏi xe hơi chạy trong bao lâu thì đuổi kịp xe đạp?
A. 1h B. 2h
C. 3h D. 4h
Đáp ánGọi t ( h ) là thời gian từ lúc xe hơi chạy đến lúc đuổi kịp xe đạp; t > 0.
⇒ t + 6 ( h ) là thời gian kể từ lúc xe đạp đi đến lúc xe hơi đuổi kịp.
+ Quãng đường xe đạp đi được là s1 = 15( t + 6 ) km.
+ Quãng đường xe hơi đi được là s2 = 60t km.
Vì hai xe xuất phát tại điểm A nên khi gặp nhau s1 = s2.
Khi đó ta có: 15(t + 6) = 60t ⇔ 60t - 15t = 90 ⇔ t = 2(h) (thỏa mãn)
Vậy xe hơi chạy được 2 giờ thì đuổi kịp xe đạp.
Chọn đáp án B.
Bài 5: Một người đi từ A đến B. Trong nửa quãng đường đầu người đó đi với vận tốc 20km/h phần đường còn lại đi với tốc độ 30km/h. Vận tốc trung bình của người đó khi đi từ A đến B là
A. 20km/h B. 20km/h
C. 25km/h D. 30km/h
Đáp ánGọi vận tốc trung bình của người đó là: x(km/h)
Gọi độ dài nửa quãng đường AB là: a(km)
Khi đó ta có:
+ Thời gian đi nửa quãng đường đầu là: a/20(h)
+ Thời gian đi nửa quãng đường sau là: a/30(h)
→ Thời gian đi cả quãng đường AB là:
Do đó ta có:
Vậy vận tốc cần tìm là 24km/h
Chọn đáp án B.
Bài 6: Một người đi xe đạp từ A đến B cách nhau 24km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4km/h so với lúc đi, nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A đến B.
A. 12km /h B. 15km/h
C. 20km/h D.16km/h
Đáp ánĐổi 30 phút = 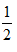
Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x > 0). Thời gian xe đi từ A đến B là 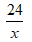
Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là 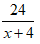
Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:
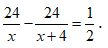
Giải phương trình:
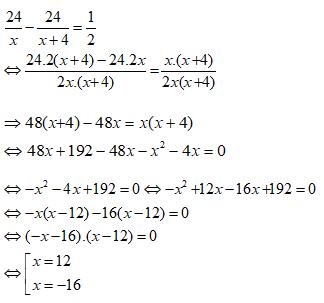
Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.
Chọn đáp án A
A. 10 B. 12
C. 15 D. 18
Đáp ánGọi số sản phẩm công nhân dự định làm trong một giờ là x (0 < x ≤ 20).
Thời gian dự kiến người đó làm xong 85 sản phẩm là 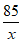
Thực tế mỗi giờ làm tăng thêm 3 sản phẩm nên số sản phẩm làm được mỗi giờ là x + 3.
Do đó 96 sản phẩm được làm trong 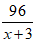
Thời gian hoàn thành công việc thực tế sớm hơn so với dự định là 20 phút = 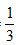
Vậy theo dự định mỗi giờ người đó phải làm 15 sản phẩm.
Chọn đáp án C
Bài 8: Một mảnh đất hình chữ nhật có độ dài đường chéo là 13m và chiều dài lớn hơn chiều rộng là 7m. Tính chiều dài của mảnh đất đó.
A. 5m B. 8m
C. 12m D. 10m
Đáp ánGọi chiều rộng của mảnh đất hình chữ nhật là x (m) (0 < x < 13)
Chiều dài mảnh đất hình chữ nhật lớn hơn chiều rộng 7m nên chiều dài của mảnh đất hình chữ nhật là x + 7 (m)
Biết độ dài đường chéo là 13m nên theo định lý Pitago ta có phương trình:
Vậy chiều rộng mảnh đất hình chữ nhật là 5m và chiều dài mảnh đất đó là 12m.
Chọn đáp án C
Bài 9: Một ô tô tải đi từ A đến B với vận tốc 45km/h. Sau 1 giờ 30 phút thì một xe con cũng xuất phát đi từ A đến B với vận tốc 60km/h và đến B cùng lúc với xe tải. Tính quãng đường AB.
A. 270 km B. 200km
C. 240 km D. 300km
Đáp ánGọi độ dài quãng đường AB là x (đơn vị km, x > 0)
Thời gian ô tô tải đi từ A đến B là 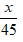
Thời gian xe con đi từ A đến B là 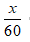
Vì xe con xuất phát sau xe tải 1 giờ 30 phút = 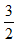
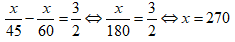
(thỏa mãn điều kiện)
Vậy độ dài quãng đường AB là 270km.
Chọn đáp án A
Bài 10: Hai bến sông A và B cách nhau 40km. Cùng một lúc với ca nô xuôi từ bến A có một chiếc bè trôi từ bến A với vận tốc 3km/h. Sau khi đến bến B, ca nô quay trở về bến A ngay và gặp bè, khi đó bè đã trôi được 8km. Tính vận tốc riêng của ca nô.
A. 20km/h B. 25km/h
C. 27 km /h D. 30km/h
Đáp ánGọi vận tốc ca nô là x(km/h), x > 3. Vận tốc ca nô xuôi dòng là x + 3(km/h)
Thời gian ca nô xuôi dòng từ A đến B là 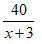
Vận tốc ca nô ngược dòng là x - 3 (km/h)
Quãng đường ca nô ngược dòng từ B đến địa điểm gặp bè là : 40 - 8 = 32 km
Thời gian ca nô ngược dòng từ B đến địa điểm gặp bè là: 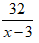
Thời gian bè trôi là:
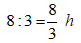
Ta có phương trình:
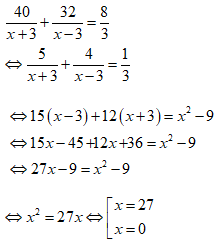
So sánh với điều kiện thì chỉ có nghiệm x = 27 thỏa mãn, suy ra vận tốc của ca nô là 27km/h.
Chọn đáp án C