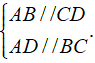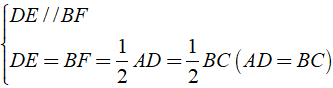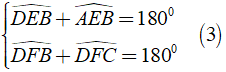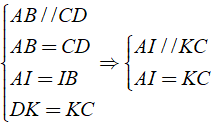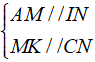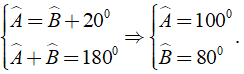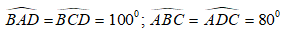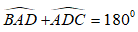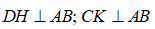Toán lớp 8 Bài 30: Hình bình hành
Lý thuyết tổng hợp Toán học lớp 8 Bài 30: Hình bình hành chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 30: Hình bình hành
A. Lý thuyết
1. Định nghĩa
Hình bình hành là tứ giác có các cạnh đối song song
Tứ giác ABCD là hình bình hành ⇔
Chú ý đặc biệt: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)
2. Tính chất hình bình hành
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết hình bình hành
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
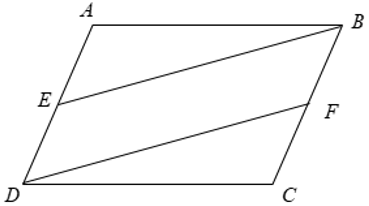
Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ABEˆ = CDFˆ .
Hướng dẫn:
Xét tứ giác BEDF có
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên BADˆ = BCDˆ ( 1 )
BEDF là hình bình hành nên BEDˆ = DFBˆ ( 2 )
Mà
Từ ( 2 ) và ( 3 ) ⇒ AEBˆ = DFCˆ ( 4 )
Xét Δ ABE có BAEˆ + AEBˆ + ABEˆ = 1800 (5)
Xét Δ DFC có DFCˆ + FCDˆ + FDCˆ = 1800 (5)
Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ABEˆ = CDFˆ (đpcm)

4. Bài tập tự luyện
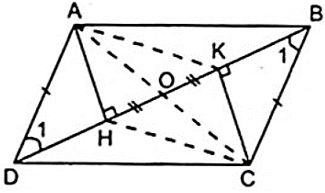
Bài 1: Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.
a) Chứng minh AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.
Hướng dẫn:
a) Từ giả thiết ta có: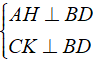
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
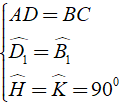
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
b) Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường
Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
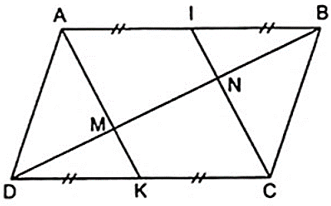
Bài 2: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:
a) AK//CI
b) DM = MN = NB
Hướng dẫn:
a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
b) Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có:
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
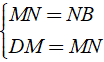
B. Bài tập trắc nghiệm
Bài 1: Chọn phương án sai trong các phương án sau?
A. Tứ giác có các cạnh đối song song là hình bình hành.
B. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
C. Tứ giác có hai góc đối bằng nhau là hình bình hành.
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Đáp án
Dấu hiệu nhận biết hình bình hành.
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
→ Đáp án C sai.
Chọn đáp án C.
Bài 2: Chọn phương án đúng trong các phương án sau.
A. Hình bình hành là tứ giác có hai cạnh đối song song.
B. Hình bình hành là tứ giác có các góc bằng nhau.
C. Hình bình hành là tứ giác có các cạnh đối song song.
D. Hình bình hành là hình thang có hai cạnh kề bằng nhau.
Đáp án
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
→ Đáp án C đúng.
Chọn đáp án C.
Bài 3: Cho hình bình hành ABCD có Aˆ = 1200, các góc còn lại của hình bình hành là?
A. Bˆ = 600, Cˆ = 1200, Dˆ = 600.
B. Bˆ = 1100, Cˆ = 800, Dˆ = 600.
C. Bˆ = 800, Cˆ = 1200, Dˆ = 800.
D. Bˆ = 1200, Cˆ = 600, Dˆ = 1200.
Đáp án
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
⇒ Aˆ = Cˆ = 1200.
Khi đó ta có: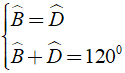
Chọn đáp án A.
Bài 4: Cho hình bình hành ABCD có Aˆ - Bˆ = 200. Xác định số đo góc A và B?
A. Aˆ = 800, Bˆ = 1000
B. Aˆ = 1000, Bˆ = 800
C. Aˆ = 800, Bˆ = 600
D. Aˆ = 1200, Bˆ = 1000
Đáp án
Theo giả thiết, ta có: Aˆ - Bˆ = 200 ⇒ Aˆ = Bˆ + 200
Mặt khác ABCD là hình bình hành nên Aˆ + Bˆ = 1800
Khi đó:
Chọn đáp án B.
Bài 5: Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
A. AC = BD
B. Δ ABD cân tại A.
C. BI là đường trung tuyến của Δ ABC
D. Aˆ + Cˆ = Bˆ + Dˆ.
Đáp án
Trong hình bình hành các góc đối bằng nhau
Hay 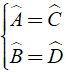
+ Δ ABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này
→ Đáp án B sai.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
→ Đáp án A sai vì theo giả thiết chưa đủ dữ kiện
Chọn đáp án C.
Bài 6: Cho tam giác ABC có M, N và P lần lượt là trung điểm AB, AC và BC. Tìm khẳng định sai ?
A. Tứ giác AMNP là hình bình hành.
B. MP // AC
C. MN = BC/2
D. Tứ giác MNCP là hình bình hành.
Đáp án
* Ta có M và N lần lượt là trung điểm của AB và AC
Suy ra: MN là đường trung bình của tam giác ABC.
⇒ MN // BC
* Vì M và P lần lượt là trung điểm của AB và BC nên MP là đường trung bình của tam giác ABC.
⇒ MP // AC
* Tứ giác MNCP có cạnh đối song song với nhau nên tứ giác MNCP là hình bình hành.
Chọn đáp án A
Bài 7: Cho hình thang ABCD có AD// BC và ∠BAD = 100o; ∠ADC = 80o. Tìm khẳng định sai
A. AB = CD; AD = BC
B. Tứ giác ABCD là hình bình hành
C.
D. AC = BD
Đáp án
* Ta có:
Và 2 góc này ở vị trí trong cùng phía nên AB// CD (1)
* Lại có: AD// BC ( giả thiết) (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).
* Suy ra: AB = CD; AD = BC;
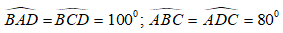
Chọn đáp án D
Bài 8: Cho hình bình hành ABCD, gọi E và F là trung điểm của AD và BC. Gọi I là giao điểm của AC và BD. Tìm khẳng định sai?
A. Tứ giác ABFE là hình bình hành
B. EI là đường trung bình của tam giác ACD
C. AI = ID
D. Tứ giác EFCD là hình bình hành
Đáp án
* Ta có ABCD là hình bình hành nên AB = CD; ABCD đồng thời là hình thang có 2 đáy là AB và CD.
Vì E và F lần lượt là trung điểm của AD và BC nên EF là đường trung bình của hình thang ABCD
Suy ra: EF// AB// CD và
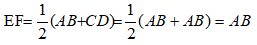
(vì AB = CD)
* Xét tứ giác ABFE có AB// EF và AE// BF nên ABFE là hình bình hành
Tương tự, tứ giác EFCD là hình bình hành.
* Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.
Tam giác ACD có E và I lần lượt là trung điểm của AD và AC nên EI là đường trung bình của tam giác
Chọn đáp án C
Bài 9: Cho hình bình hành ABCD có 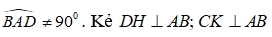
A. Tứ giác HKCD là hình bình hành.
B. AC = DK
C. ΔDHA = ΔCKB
D. HA = KB
Đáp án
* Ta có:
nên DH // CK.
Vì ABCD là hình bình hành nên AB // CD hay HK// CD.
Xét tứ giác HKCD có: DH// CK và HK// CD nên tứ giác HKCD là hình bình hành.
* Xét ΔDHA và ΔCKB có:
DH = CK (vì HKCD là hình bình hành)
AD = BC (vì ABCD là hình bình hành)
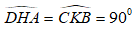
Suy ra: ΔDHA = ΔCKB (c.g.c)
Suy ra: HA = KB ( 2 cạnh tương ứng)
Chọn đáp án B
Bài 10: Cho tứ giác ABCD có: ∠A = 100o, ∠D = 80o và AB = CD. Tìm khẳng định sai?
A. AC = BD
B. Tứ giác ABCD là hình bình hành
C. AD = BC
D. ∠B = 80o, ∠C = 100o
Đáp án
* Ta có: ∠A + ∠D = 180o mà hai góc này ở vị trí trong cùng phía nên: AB // CD
* Lại có: AB = CD ( giả thiết)
Suy ra: Tứ giác ABCD là hình bình hành ( dấu hiệu nhận biết)
* Suy ra: AD = BC và ∠B = ∠D = 80o, ∠A = ∠C = 100o
Chọn đáp án A