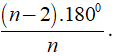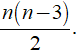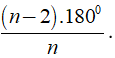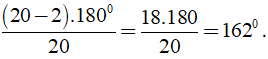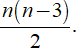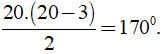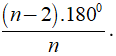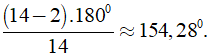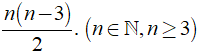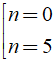Toán lớp 8 Bài 37: Đa giác. Đa giác đều
Lý thuyết tổng hợp Toán học lớp 8 Bài 37: Đa giác. Đa giác đều chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 8. Hy vọng bộ tổng hợp lý thuyết Toán lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8.
Bài 37: Đa giác. Đa giác đều
A. Lý thuyết
1. Khái niệm về đa giác
Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.

Chú ý: Từ nay nếu nhắc đến đa giác thì ta quy ước đó là đa giác lồi
2. Đa giác đều
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

3. Mở rộng
a) Góc trong đa giác
+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
+ Số đo của một góc của đa giác đều n cạnh là
b) Số đường chéo của đa giác n cạnh
Số đường chéo của đa giác n cạnh là
Ví dụ: Cho một đa giác đều có 20 cạnh. Tính số đo một góc và số đường chéo của đa giác đều đó ?
Hướng dẫn:
+ Số đo của một góc của đa giác đều n cạnh là
Khi đó số đo của một góc của đa giác đều 20 cạnh là:
+ Số đường chéo của đa giác n cạnh là
Khi đó số đường chéo của đa giác đều 20 cạnh là

4. Bài tập tự luyện
Bài 1: Cho đa giác đều có 14 cạnh. Tính :
a) Tổng số đo góc của đa giác đó
b) Số đo một góc của đa giác
c) Số đường chéo của đa giác.
Hướng dẫn:
a) Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
Tổng số đo của đa giác 14 cạnh là ( 14 - 2 ).1800 = 21600.
b) Số đo của một góc của đa giác đều n cạnh là
Số đo một góc của đa giác 14 cạnh là
c) Số đường chéo của đa giác n cạnh là
Số đường chéo của đa giác 14 cạnh là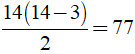
B. Bài tập trắc nghiệm
Bài 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
A. Hình vuông là đa giác đều.
B. Tổng các góc của đa giác lồi 8 cạnh là 10800.
C. Hình thoi là đa giác đều.
D. Số đo góc của hình bát giác đều là 135,50.
Đáp ánTa cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau
⇒ Hình vuông là đa giác đều.
⇒ Đáp án A đúng.
+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.
⇒ Hình thoi không phải là đa giác đều.
⇒ Đáp án C sai.
+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
Khi đó tổng các góc của đa giác lồi 8 cạnh là ( 8 - 2 ).1800 = 10800.
⇒ Đáp án B đúng.
+ Số đo của một góc của đa giác đều n cạnh là (( n - 2 ).1800)/n.
Khi đó số đo của hình bát giác đều là (( 8 - 2 ).1800)/8 = 1350.
⇒ Đáp án D sai.
Bài 2: Một đa giác 7 cạnh thì số đường chéo của đa giác đó là ?
A. 12. B. 13.
C. 14. D. Kết quả khác.
Đáp ánSố đường chéo của đa giác n cạnh là (n( n - 3 ))/2.
Khi đó số đường chéo của đa giác 7 cạnh là (7( 7 - 3 ))/2 = 14 (đường chéo)
Chọn đáp án C.
Bài 3: Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?
A. 5. B. 6.
C. 4. D. 7.
Đáp ánSố đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n2 - 3n - 2n = 0
⇔ n2 - 5n = 0 ⇔ n( n - 5 ) = 0 ⇔
So sánh điều kiện ta có n = 5 thỏa mãn.
Bài 4: Tổng số đo các góc của đa giác 12 cạnh là?
A. 1800o B.1600o
C. 1720o D. 1440o
Đáp ánTổng số đo các góc của đa giác n cạnh là (n -2).180o
Do đó, Tổng số đo các góc của đa giác 12 cạnh là (12 – 2).180o = 1800o
Chọn đáp án A
Bài 5: Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là?
A. 15 B. 16
C. 17 D. 18
Đáp ánSố đường chéo xuất phát từ 1 đỉnh của đa giác n cạnh là n – 3
Do đó, Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là: 20 – 3 = 17
Chọn đáp án C
Bài 6: Số đường chéo của đa giác 10 cạnh?
C. 70 D. 80
Đáp ánSố đường chéo xuất phát từ 1 đỉnh của đa giác 10 cạnh là: 10 – 3 = 7
Suy ra: số đường chéo của đa giác 10 cạnh là: 7.10 = 70 đường chéo
Chọn đáp án B
Bài 7: Số đo mỗi góc của 10- giác đều là:
A. 100o B. 120o
C. 136o D. 144o
Đáp ánTổng số đo các góc của 10 – giác đều là: (10 - 2). 180o = 1440o
Do đây là 10 – giác đều nên số đo các góc bằng nhau và bằng: 144o: 10 = 144o
Chọn đáp án D
Bài 8: Cho đa giác đều n cạnh. Biết số đo mỗi góc bằng 140o. Tìm n?
A. n = 9 B. n = 8
C. n = 7 D. n = 10
Đáp ánTổng số đo các góc của đa giác n cạnh là: 140.n
Mặt khác đa giác n cạnh thì có tổng số đo các góc của đa giác là: (n-2). 180
Suy ra: 140n = (n – 2). 180
⇔ 140n = 180n - 360
⇔ 40n = 360 ⇔ n = 9
Chọn đáp án A
Bài 9: Cho đa giác đều 11 cạnh có độ dài mỗi cạnh là 5cm. Tính chu vi đa giác
A. 45cm B. 50cm
C. 60cm D. 55cm
Đáp ánChu vi của đa giác đều 11 cạnh là: 5.11 = 55 cm
Chọn đáp án D
Bài 10: Hình vuông có mấy trục đối xứng?
A. 1 B. 2
C. 3 D. 4
Đáp ánHình vuông có 4 trục đối xứng bao gồm:
+ 2 đường chéo của hình vuông
+ 2 đường thẳng đi qua tâm và song song với 2 cạnh của hình vuông
Chọn đáp án D