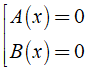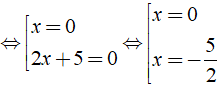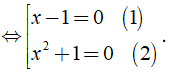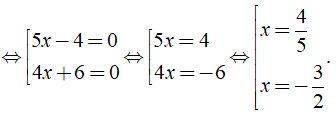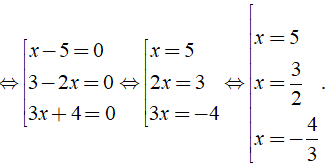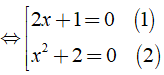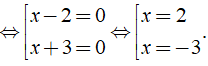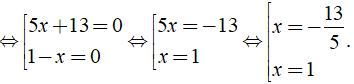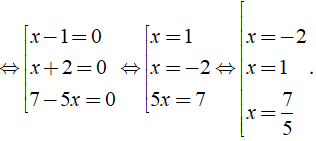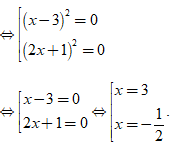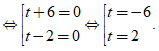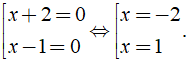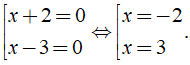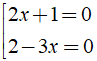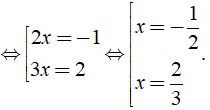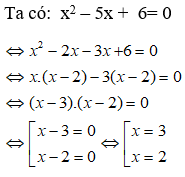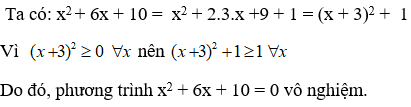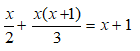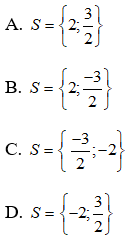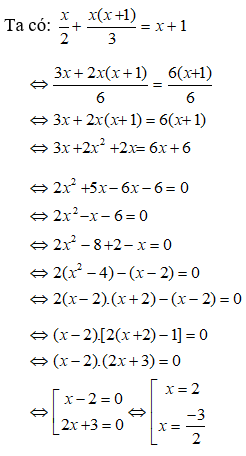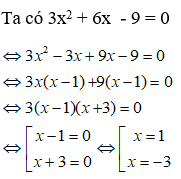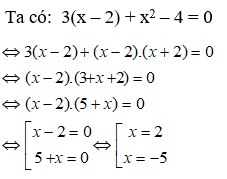Bài 46: Phương trình tích

A. Lý thuyết

1. Phương trình tích và cách giải

Cách giải phương trình tích A( x ).B( x ) = 0 ⇔ 

Cách bước giải phương trình tích

Bước 1: Đưa phương trình đã cho về dạng tổng quát A( x ).B( x ) = 0 bằng cách:

   Chuyển tất cả các hạng tử của phương trình về vế trái. Khi đó vế phải bằng 0.

   Phân tích đa thức ở vế phải thành nhân tử

Bước 2: Giải phương trình và kết luận

Ví dụ 1: Giải phương trình ( x + 1 )( x + 4 ) = ( 2 - x )( 2 + x )

Hướng dẫn:

Ta có: ( x + 1 )( x + 4 ) = ( 2 - x )( 2 + x ) ⇔ x² + 5x + 4 = 4 - x²

⇔ 2x² + 5x = 0 ⇔ x( 2x + 5 ) = 0

Vậy phương trình đã cho có tập nghiệm là S = { - 5/2; 0 }

Ví dụ 2: Giải phương trình x³ - x² = 1 - x

Hướng dẫn:

Ta có: x³ - x² = 1 - x ⇔ x²( x - 1 ) = - ( x - 1 )

⇔ x²( x - 1 ) + ( x - 1 ) = 0 ⇔ ( x - 1 )( x² + 1 ) = 0

( 1 ) ⇔ x - 1 = 0 ⇔ x = 1.

( 2 ) ⇔ x² + 1 = 0 (Vô nghiệm vì x² ≥ 0 ⇒ x² + 1 ≥ 1 )

Vậy phương trình đã cho có tập nghiệm là S = { 1 }.

2. Bài tập tự luyện

a) ( 5x - 4 )( 4x + 6 ) = 0

b) ( x - 5 )( 3 - 2x )( 3x + 4 ) = 0

c) ( 2x + 1 )( x² + 2 ) = 0

d) ( x - 2 )( 3x + 5 ) = ( 2x - 4 )( x + 1 )

Hướng dẫn:

a) Ta có: ( 5x - 4 )( 4x + 6 ) = 0

Vậy phương trình đã cho có tập nghiệm là S = { - 3/2; 4/5 }.

b) Ta có: ( x - 5 )( 3 - 2x )( 3x + 4 ) = 0

Vậy phương trình đã cho có tập nghiệm là S = { - 4/3; 3/2; 5 }.

c) Ta có: ( 2x + 1 )( x² + 2 ) = 0

Giải ( 1 ) ⇔ 2x + 1 = 0 ⇔ 2x = - 1 ⇔ x = - 1/2.

Ta có: x² ≥ 0 ⇒ x² + 2 ≥ 2 ∀ x ∈ R

⇒ Phương trình ( 2 ) vô nghiệm.

Vậy phương trình đã cho có tập nghiệm S = { - 1/2 }.

d) Ta có: ( x - 2 )( 3x + 5 ) = ( 2x - 4 )( x + 1 )

⇔ ( x - 2 )( 3x + 5 ) - 2( x - 2 )( x + 1 ) = 0

⇔ ( x - 2 )[ ( 3x + 5 ) - 2( x + 1 ) ] = 0

⇔ ( x - 2 )( x + 3 ) = 0

Vậy phương trình đã cho có tập nghiệm là S = { - 3;2 }.

Bài 2: Giải các phương trình sau:

a) ( 2x + 7 )² = 9( x + 2 )²

b) ( x² - 1 )( x + 2 )( x - 3 ) = ( x - 1 )( x² - 4 )( x + 5 )

c) ( 5x² - 2x + 10 )² = ( 3x² + 10x - 8 )²

d) ( x² + x )² + 4( x² + x ) - 12 = 0

Hướng dẫn:

a) Ta có: ( 2x + 7 )² = 9( x + 2 )²

⇔ ( 2x + 7 )² - 9( x + 2 )² = 0

⇔ [ ( 2x + 7 ) + 3( x + 2 ) ][ ( 2x + 7 ) - 3( x + 2 ) ] = 0

⇔ ( 5x + 13 )( 1 - x ) = 0

Vậy phương trình đã cho có tập nghiệm là S = { - 13/5; 1 }.

b) Ta có: ( x² - 1 )( x + 2 )( x - 3 ) = ( x - 1 )( x² - 4 )( x + 5 )

⇔ ( x² - 1 )( x + 2 )( x - 3 ) - ( x - 1 )( x² - 4 )( x + 5 ) = 0

⇔ ( x - 1 )( x + 1 )( x + 2 )( x - 3 ) - ( x - 1 )( x - 2 )( x + 2 )( x + 5 ) = 0

⇔ ( x - 1 )( x + 2 )[ ( x + 1 )( x - 3 ) - ( x - 2 )( x + 5 ) ] = 0

⇔ ( x - 1 )( x + 2 )[ ( x² - 2x - 3 ) - ( x² + 3x - 10 ) ] = 0

⇔ ( x - 1 )( x + 2 )( 7 - 5x ) = 0

Vậy phương trình có tập nghiệm là S = { - 2; 1; 7/5 }.

c) Ta có: ( 5x² - 2x + 10 )² = ( 3x² + 10x - 8 )²

⇔ ( 5x² - 2x + 10 )² - ( 3x² + 10x - 8 )² = 0

⇔ [ ( 5x² - 2x + 10 ) - ( 3x² + 10x - 8 ) ][ ( 5x² - 2x + 10 ) + ( 3x² + 10x - 8 ) ] = 0

⇔ ( 2x² - 12x + 18 )( 8x² + 8x + 2 ) = 0

⇔ 4( x² - 6x + 9 )( 4x² + 4x + 1 ) = 0

⇔ 4( x - 3 )²( 2x + 1 )² = 0

Vậy phương trình đã cho có tập nghiệm S = {- 1/2; 3}.

d) Ta có: ( x² + x )² + 4( x² + x ) - 12 = 0

Đặt t = x² + x, khi đó phương trình trở thành:

t² + 4t - 12 = 0 ⇔ ( t + 6 )( t - 2 ) = 0

+ Với t = - 6, ta có: x² + x = - 6 ⇔ x² + x + 6 = 0 ⇔ ( x + 1/2 )² + 23/4 = 0

Mà ( x + 1/2 )² + 23/4 ≥ 23/4 ∀ x ∈ R ⇒ Phương trình đó vô nghiệm.

+ Với t = 2, ta có x² + x = 2 ⇔ x² + x - 2 = 0

⇔ ( x + 2 )( x - 1 ) = 0 ⇔ 

Vậy phương trình có tập nghiệm là S = { - 2;1 }.

B. Bài tập trắc nghiệm

Bài 1: Nghiệm của phương trình ( x + 2 )( x - 3 ) = 0 là?

   A. x = - 2.   B. x = 3.

   C. x = - 2; x = 3.   D. x = 2.

Bài 2: Tập nghiệm của phương trình ( 2x + 1 )( 2 - 3x ) = 0 là?

   A. S = { - 1/2 }.   B. S = { - 1/2; 3/2 }

   C. S = { - 1/2; 2/3 }.   D. S = { 3/2 }.

Bài 3: Nghiệm của phương trình 2x( x + 1 ) = x² - 1 là?

   A. x = - 1.   B. x = ± 1.

   C. x = 1.   D. x = 0.

Bài 4: Giá trị của m để phương trình ( x + 2 )( x - m ) = 4 có nghiệm x = 2 là?

   A. m = 1.   B. m = ± 1.

   C. m = 0.   D. m = 2.

Bài 5: Giá trị của m để phương trình x³ - x² = x + m có nghiệm x = 0 là?

   A. m = 1.   B. m = - 1.

   C. m = 0.   D. m = ± 1.

Bài 6: Giải phương trình: x² - 5x + 6 = 0

A. x = 3 hoặc x = 2

B. x= -2 hoặc x = -3

C. x = 2 hoặc x = -3

D. x = -2 hoặc x = 3

Bài 7: Số nghiệm của phương trình x² + 6x + 10 = 0

A. 1             B. 2

C. 0             D. Vô nghiệm

Bài 8: Giải phương trình:

Bài 9: Giải phương trình : 3x² + 6x - 9 = 0

A. x = 1

B. x = 1 hoặc x = -3

C. x = 1 hoặc x = -2

D. x = -3 hoặc x = -2

Bài 10: Giải phương trình: 3(x - 2) + x² - 4 = 0

A. x = 1 hoặc x = 2

B. x = 2 hoặc x = -5

C. x = 2 hoặc x = - 3

D. Đáp án khác