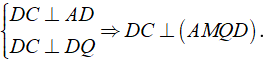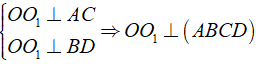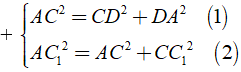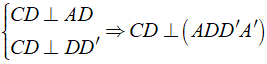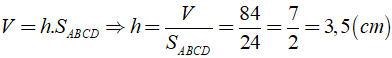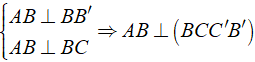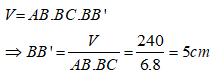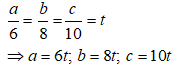Bài 67: Thể tích của hình hộp chữ nhật

A. Lý thuyết

1. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc

a) Đường thẳng vuông góc với mặt phẳng

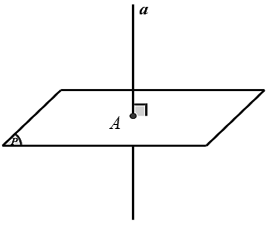
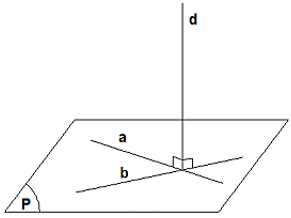
– Đường thẳng d gọi là vuông góc với mặt phẳng ( P ) nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng ( P ). Kí hiệu d ⊥ ( P ).

– Nếu một đường thẳng a vuông góc với mặt phẳng ( P ) tại điểm A thì nó vuông góc với mọi đường thẳng nằm trong ( P ) và đi qua điểm A.

b) Hai mặt phẳng vuông góc

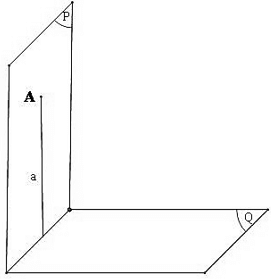
– Mặt phẳng ( P ) gọi là vuông góc với mặt phẳng ( Q ) nếu mặt phẳng ( P ) chứa đường thẳng vuông góc với mặt phẳng ( Q ). Kí hiệu ( Q ) ⊥ ( P ).

c) Ví dụ áp dụng

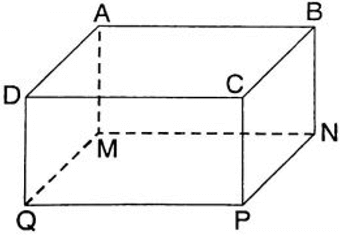
Ví dụ: Cho hình hộp chữ nhật ABCD.MNPQ. Chứng minh rằng ( AMQD ) ⊥ ( CPQD )

Hướng dẫn:

Ta có:

Mà DC ∈ ( DCPQ ) ⇒ ( AMQD ) ⊥ ( DCPQ )

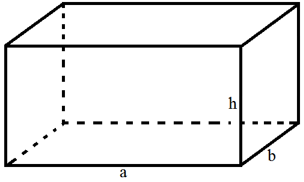
2. Thể tích hình hộp chữ nhật

a) Thể tích hình hộp chữ nhật

Ta có V = a.b.h

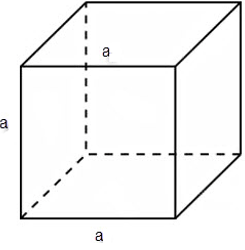
b) Thể thích hình lập phương

Ta có: V = a³.

c) Ví dụ áp dụng

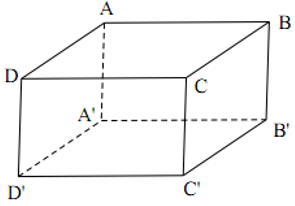
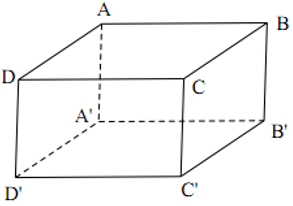
Ví dụ: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm. Tính thể tích hình hộp chữ nhật ABCD.A'B'C'D'.

Hướng dẫn:

Ta có V_{ABCD.A'B'C'D'} = AB.AD.AA' = 12.16.25 = 4800( cm³ ).

3. Bài tập tự luyện

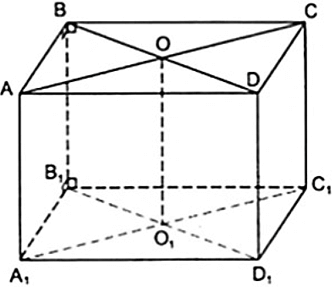
Bài 1: Cho hình hộp chữ nhật ABCD.A₁B₁C₁D₁ có ABCD là hình vuông. Gọi O là giao điểm của AC và BD, O₁ là giao điểm của A₁C₁ và B₁D₁. Chứng minh rằng:

a) BDD₁B₁ là hình chữ nhật.

b) OO₁ ⊥ ( ABCD )

Hướng dẫn:

a) Từ giả thiết ABCD.A₁B₁C₁D₁ là hình hộp chữ nhật nên các mặt bên ( BB₁A₁A ),( BB₁C₁C ) là hình chữ nhật, do đó ta có:

 ⇒ BB₁ ⊥ mp( ABCD )

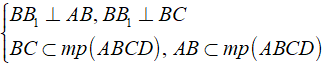
Mặt khác đường chéo BD ⊂ mp( ABCD ) và đi qua B nên:

BB₁ ⊥ BD ⇒ Bˆ₁BD = 90⁰

Chứng minh tương tự như trên, ta cũng được: BB₁D₁ˆ = BDD₁ˆ = 90⁰

Điều đó chứng tỏ tứ giác BDD₁B₁ có ba góc vuông nên là hình chữ nhật.

b) Chứng minh tương tự như câu a, ta có tứ giác ACC₁A₁ là hình chữ nhật

Áp dụng tính chất đường chéo và các hình vuông ABCD, A₁B₁C₁D₁ ta được O là trung điểm của AC và BD và O₁ là trung điểm của A₁C₁ và B₁D₁

⇒ OO₁ là đường trung bình của các hình chữ nhật BDD₁B₁ và ACC₁A₁

Do đó: OO₁//BB₁//DD₁//AA₁//CC₁

Suy ra

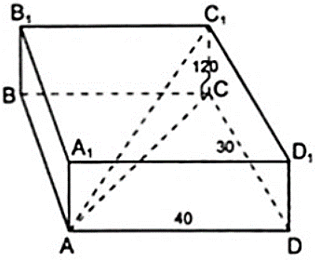
Bài 2: Các kích thức của hình hộp chữ nhật như trên hình vẽ. Tính độ dài của đoạn AC₁ ?

Hướng dẫn:

Vì ABCD.A₁B₁C₁D₁ là hình hộp chữ nên

CC₁ ⊥ mp( ABCD ) ⇒ CC₁ ⊥ AC hay tam giác ACC₁ vuông tại C, đáy ABCD là hình chữ nhật nên tam giác ACD vuông tại D.

Áp dụng định lý Py – ta – go ta có:

Thay đẳng thức ( 1 ) vào ( 2 ) ta được:

AC₁² = CD² + AD² + CC₁² ⇒ AC₁ = √ (CD² + AD² + CC₁²)

Hay AC₁ = √ (30² + 40² + 120²) = √ (130²) = 130( cm )

B. Bài tập trắc nghiệm

Bài 1: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chọn phát biểu đúng?

   A. CD ⊥ (A'B'C'D')

   B. DC ⊥ (ADD'A')

   C. A'D' ⊥ (BCC'B')

   D. CC' ⊥ (AA'B'B)

Bài 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2cm, AD = 3cm, AA' = 4cm. Thể tích hình hộp chữ nhật ABCD.A'B'C'D' ?

   A. 12( cm³ )   B. 24( cm³ )

   C. 18( cm³ )   D. 15( cm³ )

Bài 3: Cho hình lập phương có các cạnh có độ dài là 5cm. Thể tích của hình lập phương đó là?

   A. 100( cm³ )   B. 115( cm³ )

   C. 125/3( cm³ )   D. 125( cm³ )

Bài 4: Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích đáy S_ABCD = 24cm² và có thể tích V = 84( cm³ ). Chiều cao của hình hộp chữ nhật có độ dài là?

   A. h = 4( cm )   B. h = 3,5( cm )

   C. h = 5( cm )   D. h = 2( cm )

Bài 5: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chọn phát biểu đúng trong các phát biểu sau:

   A. ( ABCD ) ⊥ ( A'B'C'D' )

   B. ( ADD'A' ) ⊥ ( BCC'B' )

   C. ( ABB'A' ) ⊥ ( BCC'B' )

   D. ( ABB'A' ) ⊥ ( CDD'C' )

Bài 6: Cho hình hộp chữ nhật ABCD. MNPQ có AB = 6cm; BC = 8cm và thể tích của hình hộp là 240cm³. Tính AA’

   A. 5cm     B. 6cm

   C. 8cm     D. 10cm

Bài 7: Cho hình lập phương có thể tích là: 64cm³. Tính diện tích 1 mặt của hình lập phương?

   A. 8cm²     B. 12cm²

   C. 16cm²     D. 64cm²

Bài 8: Cho hình lập phương có diện tích 1 mặt bên 36cm². Tính thể tích của hình lập phương?

   A. 108cm³     B. 144cm³

   C. 125cm³     D. 216cm³

Bài 9: Cho một hình hộp chữ nhật có các kích thước tỉ lệ với 6; 8; 10 và thể tích của hình hộp là 480cm³. Khi đó, kích thước lớn nhất của hình hộp là:

   A. 12cm     B. 15cm

   C. 10cm     D. 20cm

Bài 10: Diện tích toàn phần của hình lập phương là 294 cm². Tính thể tích của nó?

   A. 343 cm³     B. 300cm³

   C. 320 cm³     D. 280cm³