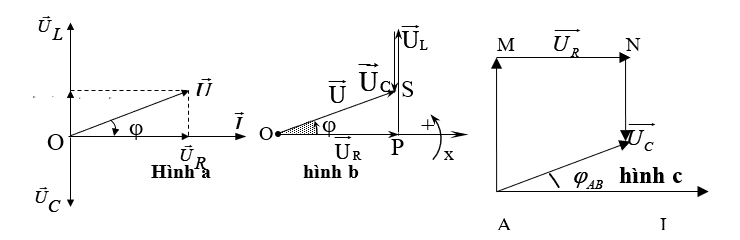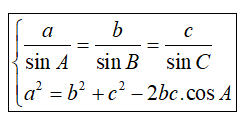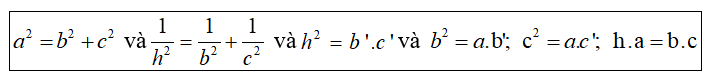Cách giải bài toán điện xoay chiều bằng Phương pháp giản đồ vectơ

I. Phương pháp

1. Các quy tắc cộng véc tơ

a) Quy tắc tam giác

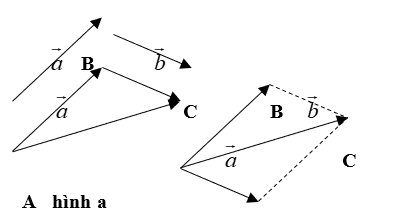
Nội dung của quy tắc tam giác là: Từ điểm A tuỳ ý ta vẽ véc tơ AB = a , rồi từ điểm B ta vẽ véc tơ BC = b . Khi đó véc tơ AC được gọi là tổng của hai véc tơ a và b (Xem hình a) .

b) Quy tắc hình bình hành

Nội dung của quy tắc hình bình hành là: Từ điểm A tuỳ ý ta vẽ hai véc tơ AB = a và véc tơ AD = b , sau đó dựng điểm C sao cho ABCD là hình bình hành thì véc tơ AC được gọi là tổng của hai véc tơ a và b (xem hình b) . Ta thấy khi dùng quy tắc hình bình hành các véc tơ đều có chung một gốc A nên gọi là các véc tơ buộc.

Vận dụng quy tắc hình bình hành để cộng các véc tơ trong bài toán điện xoay chiều ta có phương pháp véc tơ buộc, còn nếu vận dụng quy tắc tam giác thì ta có phương pháp véc tơ trượt (“các véc tơ nối đuôi nhau”).

2. Cơ sở vật lí của phương pháp giản đồ véc tơ

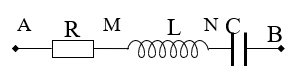
Xét mạch điện như hình a hoặc hình b. Đặt vào 2 đầu đoạn AB một điện áp xoay chiều. Tại một thời điểm bất kì, cường độ dòng điện ở mọi chỗ trên mạch điện là như nhau. Nếu cường độ dòng điện đó có biểu thức là: i = I_ocosωt (A) thì biểu thức điện áp giữa hai điểm AM, MN và NB lần lượt là:

    + Do : U_AB = U_AM + U_MN + U_NB .

    + Các đại lượng biến thiên điều hoà cùng tần số nên chúng có thể biểu diễn bằng các véc tơ Frexnel:

(trong đó độ lớn của các véc tơ biểu thị điện áp hiệu dụng của nó).

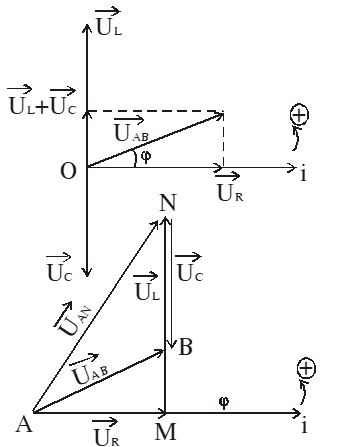
Cách vẽ giản đồ véc tơ cùng gốc: Vì i không đổi nên ta chọn trục cường độ dòng điện làm trục gốc, gốc tại điểm O, chiều dương là chiều quay lượng giác.( H.1)

- Chọn trục ngang là trục cường độ d điện

- Chọn gốc A

- Vẽ các vectơ nối duôi , hoặc vẽ cùng chung gốc O( là A)

Để thực hiện cộng các véc tơ trên ta phải vận dụng một trong hai quy tắc cộng véc tơ.

Chú ý: Vẽ giản đồ vectơ cùng gốc khi có sự bắt chéo RL với RC

Vectơ U_AM, U_MN, U_NB nối đuôi nhau theo nguyên tắc: R - đi ngang; L - đi lên; C - đi xuống.

Bước 3: Nối A với B thì véc tơ AB biểu diễn điện áp u_AB. Tương tự, véc tơ AN biểu diễn điện áp U_AN, véc tơ MB biểu diễn điện áp U_NB. Véc tơ AB chính là biểu diễn U_AB

Một số điểm cần lưu ý:

- Các điện áp trên các phần tử được biểu diễn bởi các vectơ mà độ lớn của các vectơ tỉ lệ với điện áp hiệu dụng của nó.

- Độ lệch pha giữa các điện áp là góc hợp bởi giữa các vectơ tương ứng biểu diễn chúng. Độ lệch pha giữa điện áp và cường độ dòng điện là góc hợp bởi vectơ biểu diễn nó với trục I. Véc tơ “nằm trên” (hướng lên trên) sẽ nhanh pha hơn véc tơ “nằm dưới” (hướng xuống dưới).

- Độ dài cạnh của tam giác trên giản đồ biểu thị điện áp hiệu dụng, độ lớn góc biểu thị độ lệch pha.

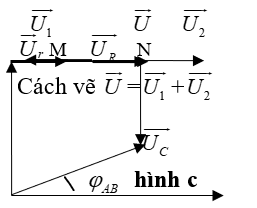
- Cộng hai véc tơ cùng phương ngược chiều U₁, U₁ thành U theo quy tắc hình bình hành (xem hình trên).

    + Nếu cuộn dây không thuần cảm (trên đoạn AM có cả L và r (Xem hình a dưới đây)) thì U_AB = U_L + U_r + U_R + U_C ta vẽ L trước như sau: L - đi lên, r - đi ngang, R - đi ngang và C - đi xuống (xem hình B. hoặc vẽ r trước như sau: r - đi ngang, L - đi lên, R - đi ngang và C - đi xuống (Xem hình c )

    + Nếu mạch điện có nhiều phần tử (Xem hình a) thì ta cũng vẽ được giản đồ một cách đơn giản như phương pháp đã nêu (Xem hình d).

    + Góc hợp bởi hai vec tơ a và b là góc BAD (nhỏ hơn 180 ^ο). Việc giải các bài toán là nhằm xác định độ lớn các cạnh và các góc của các tam giác hoặc tứ giác, nhờ các hệ thức lượng trong tam giác vuông, các hệ thức lượng giác, các định lí hàm số sin, hàm số cos và các công thức toán học.

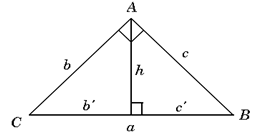
    + Trong toán học một tam giác sẽ giải được nếu biết trước 3 (hai cạnh một góc, hai góc một cạnh, ba cạnh) trong số 6 yếu (ba góc trong và ba cạnh). Để làm điều đó ta sử dụng các định lí hàm số sin và định lí hàm số cosin (xem hình bên).

Các công thức thường dùng cho tam giác vuông:

một số hệ thức trong tam giác vuông:

Tìm trên giản đồ véctơ tam giác biết trước ba yếu tố (hai cạnh một góc, hai góc một cạnh), sau đó giải tam giác đó để tìm các yếu tố chưa biết, cứ tiếp tục như vậy cho các tam giác còn lại.

2. Ví dụ

Ví dụ 1: Cho mạch điện xoay chiều gồm R,L,C nối tiếp .Các điện áp ở hai đầu đoạn mạch : U = 120V ; 2 đầu cuộn dây U_d = 120V; ở hai đầu tụ điện U_C = 120V.

Xác định hệ số công suất của mạch ?

A. 1/2          B. √3/2

C. 1          D. 1 / √3

Hướng dẫn:

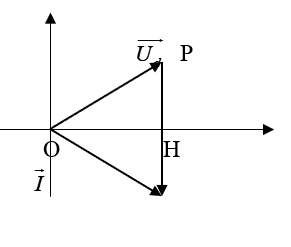
Ta vẽ giản đồ vectơ có: U = 120V; 2 đầu cuộn dây U_d = 120V ;

ở hai đầu tụ điện U_C = 120V. Thấy tam giác OPQ đều nên POH = POQ / 2 = π / 6 = φ_d ;

HOQ = π / 6 ⇒ φ = -π/3 ⇒ cosφ = OH / OQ = √3/2

Chọn đáp án B

Ví dụ 2: Cho mạch điện xoay chiều như hình vẽ. Cuộn dây thuần cảm. Cho biết điện áp hiệu dụng giữa hai điểm A, B là U_AB = 200 V , giữa hai điểm A, M là U_AM = 200√2 V và giữa M, B là U_MB = 200 V . Tính điện áp hiệu dụng giữa hai đầu điện trở và hai đầu tụ điện.

Hướng dẫn:

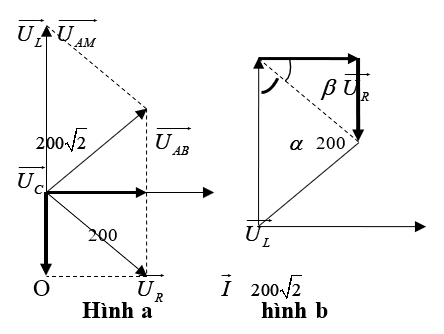
Cách 1: Phương pháp véctơ chung gốc (xem hình a).

    + Vì U_AB = U_MB = 200 V nên tam giác OU_ABU_MB là tam giác cân tại O. Chú ý 200² + 200² = (200√2)² nên tam giác đó là tam giác vuông cân tại O.

    + Do đó tam giác OU_RU_MB cũng là tam giác vuông cân tại U_R: ⇒ U_R = U_C = U_MB / 2 = 100√2 .

Cách 2: Phương pháp véctơ trượt (xem hình b).

    + Dễ thấy 200² + 200² = (200√2)² nên ΔABM vuông cân tại B, suy ra α = 45^ο ⇒ β= 45^ο → ΔMNB vuông cân tại N ⇒ U_R = U_C = MB / √2 = 100√2

Đáp số: U_R = U_C = 100√2