Cách tìm số lần vật đi qua vị trí có li độ x, có vận tốc v từ thời điểm t1 đến t2 hay, chi tiết

1. Phương pháp

* Giải phương trình lượng giác được các nghiệm

* Từ t₁ < t ≤ t₂ ⇒ Phạm vi giá trị của (với k ∈ Z)

* Tổng số giá trị của k chính là số lần vật đi qua vị trí đó.

Lưu ý:

+ Có thể giải bài toán bằng cách sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.

+ Trong mỗi chu kỳ (mỗi dao động) vật qua mỗi vị trí biên 1 lần còn các vị trí khác 2 lần.

2. Ví dụ

Ví dụ 1: Vật dao động điều hòa với phương trình : 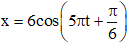 (1).

a) Trong khoảng thời gian 2,5 s vật qua vị trí x = 3 cm mấy lần.

b) Trong khoảng thời gian 2,0 s vật qua vị trí x = 4 cm theo chiều dương mấy lần.

c) Trong khoảng thời gian 2,5 s vật qua vị trí cân bằng theo chiều dương mấy lần.

d) Trong khoảng thời gian 2,86 s vật qua vị trí cân bằng mấy lần.

Hướng dẫn:

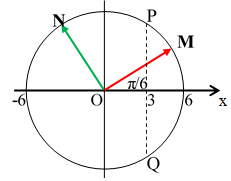
Trước tiên ta biểu diễn phương trình (1) trên vòng tròn, với φ = π/6 rad.

Vật xuất phát từ M, theo chiều âm.

a) Trong khoảng thời gian Δt = 2,5s

⇒ góc quét Δφ = Δt.ω = 2,5.5π = 12,5π = 6.2π + π/2

Từ vòng tròn ta thấy:

Trong một chu kỳ vật qua x = 3cm được 2 lần tại P(chiều âm) và Q(chiều dương)

Trong Δφ₁ = 6.2π ; 6 chu kỳ vật qua x = 3cm được 6.2 = 12 lần

Còn lại Δφ₂ = π/2 từ M → N vật qua x = 3cm một lần tại P(chiều âm).

Vậy: Trong khoảng thời gian Δt = 2,5s vật qua x = 3cm được 12 + 1 = 13 lần.

b. Trong khoảng thời gian Δt = 2 s

⇒ góc quét Δφ = Δt.ω = 2.5π = 10π = 5.2π

Vật thực hiện được 5 chu kỳ (quay được 5 vòng)

Từ vòng tròn ta thấy:

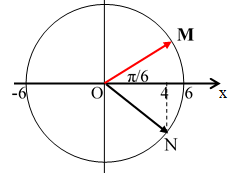
Trong một chu kỳ vật qua vị trí x = +4cm theo chiều dương được một lần (tại N)

Vậy: trong 5 chu kỳ thì vật qua vị trí x = 4cm theo chiều dương được 5 lần.

c. Trong khoảng thời gian Δt = 2,5s

⇒ góc quét Δφ = Δt.ω = 2,5.5π = 12,5π = 6.2π + π/2

Từ vòng tròn ta thấy:

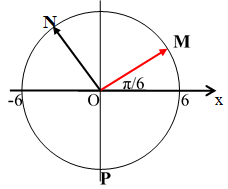
Trong một chu kỳ vật qua vị trí cân bằng theo chiều dương 1 lần tại P.

Trong Δφ₁ = 6.2π ; 6 chu kỳ vật qua vị trí cân bằng theo chiều dương 6 lần tại P.

Còn lại Δφ₂ = π/2 từ M → N vật qua không qua vị trí cân bằng theo chiều dương lần nào. Vậy trong khoảng thời gian Δt = 2,5s vật qua vị trí cân bằng theo chiều dương 6 lần.

d) Trong khoảng thời gian Δt = 2,86s

⇒ góc quét Δφ = Δt.ω = 2,86.5π = 14,3π = 7.2π + 0,3π

Từ vòng tròn ta thấy:

Trong một chu kỳ vật qua vị trí cân bằng 2 lần tại P_{(chiều âm)} và Q_{(chiều dương)}.

Trong Δφ₁ = 7.2π; 7 chu kỳ vật qua vị trí cân bằng 14 lần tại P và Q.

Còn lại Δφ₂ = 0,3π từ M → N vật qua không qua vị trí cân bằng lần nào.

Vậy trong khoảng thời gian Δt = 2,86s vật qua vị trí cân bằng 15 lần.