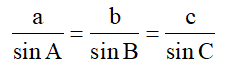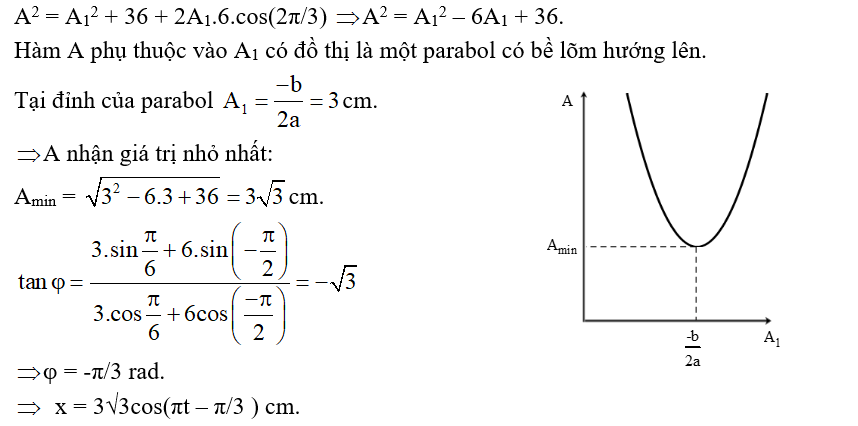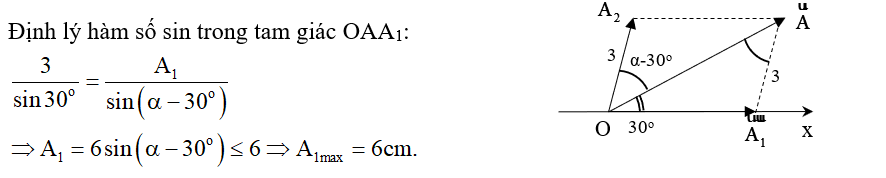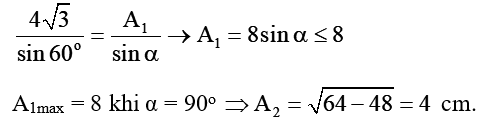Cách tìm điều kiện để biên độ A, A1, A2 đạt cực đại, cực tiểu hay, chi tiết

1. Phương pháp

- Dựng các véc tơ A₁, A₂, A hoặc xây dựng được các biểu thức thể hiện mối quan hệ giữa đại lượng cần đánh giá cực trị với các đại lượng khác.

- Dựa vào yêu cầu của bài toán áp dụng định lí Sin trong tam giác

Hoặc sử dụng các bất đẳng thức như cosin, Bunhiacopxki, cực trị của hàm số để suy ra điều kiện cần tìm.

- Áp dụng các hệ thức lượng trong tam giác để tính toán kết quả.

2. Ví dụ

Ví dụ 1: Câu 18 – ĐH2012 – M371. Cho x₁ = A₁cos(πt + π/6) cm và x₂ = 6cos(πt – π/2) cm là phương trình của hai dao động cùng phương. Dao động tổng hợp của hai dao động này có phương trình x = Acos(πt + φ) cm. Thay đổi A₁ cho đến khi biên độ A đạt giá trị cực tiểu thì

A. φ = 0 rad.          B. φ = –π/3 rad.          C. φ = –π/6 rad.          D. φ = π rad.

Hướng dẫn:

Ví dụ 2: Một chất điểm tham gia đồng thời hai dao động cùng phương. Phương trình ly độ của các dao động thành phần và dao động tổng hợp lần lượt là x₁ = A₁cos(ωt) cm; x₂ = 3cos(ωt + α) cm; và x = Acos(ωt+ π/6) cm. Biên độ dao động A1 có giá trị lớn nhất là

A. 9 cm.          B. 6 cm.          C. 8 cm.          D. 12 cm.

Hướng dẫn:

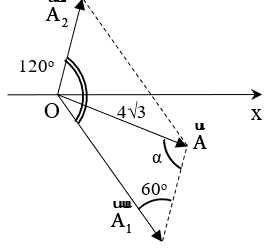
Ví dụ 3: Một chất điểm tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có phương trình là x₁ = A₁cos(ωt – π/3) và x₂ = A₂cos(ωt + π/3). Dao động tổng hợp có biên độ 4√3 cm. Khi A₁ đạt giá trị cực đại thì A₂ có giá trị là

A. 2 cm.          B. 3 cm.          C. 5 cm.          D. 4 cm.

Hướng dẫn:

Khi A₁ đạt giá trị cực đại

Độ lệch pha Δφ = π/3 – (-π/3) = 2π/3.

Áp dụng định lí hàm số sin trong tam giác OAA1: