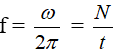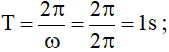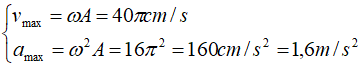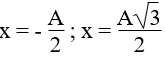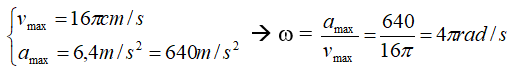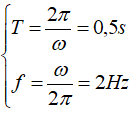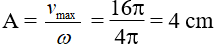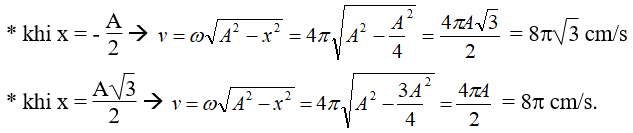Cách xác định các đại lượng đặc trưng trong dao động điều hòa

1. Phương pháp

Xác định các đại lượng như biên độ A, vận tốc góc ω, chu kỳ, tần số, pha ban đầu, ... bằng cách đồng nhất với phương trình chuẩn của dao động điều hòa.

- Dao động điều hòa là dao động mà li độ của vật được biểu thị bằng hàm cosin hay sin theo thời gian.

Hoặc là nghiệm của phương trình vi phân: x’’ + ω²x = 0 có dạng như sau:

x = Acos(ωt + φ)

Trong đó:

x: Li độ, li độ là khoảng cách từ vật đến vị trí cân bằng ( Đơn vị độ dài)

A: Biên độ (li độ cực đại) ( Đơn vị độ dài)

ω: Vận tốc góc (rad/s)

ωt + φ: Pha dao động (rad/s) tại thời điểm t, cho biết trạng thái dao động của vật ( gồm vị trí và chiều )

φ: Pha ban đầu (rad) tại thời điểm t = 0s, phụ thuộc vào cách chọn gốc thời gian, gốc tọa độ.

φ, A là những hằng số dương;

- Phương trình vận tốc v (m/s)

v = x’ = v = - Aωsin(ωt + φ) = ωAcos(ωt + φ + π/2 )

→ v_max = ωA Tại vị trí cân bằng x = 0

v_min = 0 Tại 2 biên x = 2 hoặc x = -2.

Nhận xét: Trong dao động điều hoà vận tốc sớm pha hơn li độ góc π/2.

- Phương trình gia tốc a (m/s²)

a = v’ = x’’ = a = - ω²Acos(ωt + φ) = - ω²x = ω²Acos(ωt + φ + π/2)

→ a_max = ω²A tại 2 biên

a_min = 0 tại vtcb x = 0

Nhận xét: Trong dao động điều hoà gia tốc sớm pha hơn vận tốc góc π/2 và ngược pha với li độ.

- Chu kỳ: 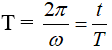 . Trong đó (t: thời gian; N là số dao động thực hiện trong khoảng thời gian t)

“Thời gian để vật thực hiện được một dao động hoặc thời gian ngắn nhất để trạng thái dao động lặp lại như cũ.”

- Tần số: 

“Tần số là số dao động vật thực hiện được trong một giây (số chu kỳ vật thực hiện trong một giây).”

2. Ví dụ

Ví dụ 1: Một vật dao động điều hòa với phương trình x = 4cos(2πt + π/2) cm. Xác định biên độ, chu kỳ và vị trí ban đầu của vật?

Hướng dẫn:

Đồng nhất phương trình với phương trình chuẩn dao động điều hòa x = Acos(ωt + φ), ta được:

A = 4; ω = 2π → 

Thời điểm ban đầu là lúc t = 0, thay vào phương trình, được x = 4cos (π/2) = 0, thời điểm ban đầu vật đang ở vị trí cân bằng.

Ví dụ 2: Một vật dao động điều hòa với biên độ 10 cm. Trong khoảng thời gian 90 giây, vật thực hiện được 180 dao động. Lấy π² = 10.

a) Tính chu kỳ, tần số dao động của vật.

b) Tính tốc độ cực đại và gia tốc cực đại của vật.

Hướng dẫn:

a) Ta có Δt = N.T → T = Δt/N = 90/180 = 0,5 s

Từ đó ta có tần số dao động là f = 1/T = 2 (Hz).

b) Tần số góc dao động của vật là

Tốc độ cực đại, gia tốc cực đại của vật được tính bởi công thức

Ví dụ 3: Một vật dao động điều hòa có v_max = 16π (cm/s); a_max = 6,4 (m/s² ). Lấy π² = 10.

a) Tính chu kỳ, tần số dao động của vật.

b) Tính độ dài quỹ đạo chuyển động của vật.

c) Tính tốc độ của vật khi vật qua các li độ 

Hướng dẫn:

a) Ta có

Từ đó ta có chu kỳ và tần số dao động là:

b) Biên độ dao động A thỏa mãn 

→ Độ dài quỹ đạo chuyển động là 2A = 8 (cm).

c) Áp dụng công thức tính tốc độ của vật ta được: