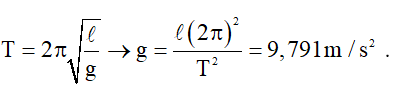Cách giải bài toán Con lắc trùng phùng hay, chi tiết

1. Phương pháp

♦ Một con lắc đơn A có chu kì T dao động trước mặt một con lắc đồng hồ gõ giây B (chu kì T’ = 2s). Khi hai con lắc cùng đi qua vị trí cân bằng theo cùng một chiều ta bảo hai con lắc trùng phùng. Gọi Δt là thời gian ngăn cách giữa hai lần trùng phùng liên tiếp.

Số dao động mà con lắc B làm được trong thời gian Δt là

Δt = N.T’ = 2N → N = Δt/2

• Nếu T rất gần và nhỏ hơn T’ thì tổng thời gian Δt con lắc A sẽ làm được N + 1 dao động.

• nếu T rất gần và lớn hơn T’ thì trong khoảng thời gian Δt con lắc A sẽ làm được N – 1 dao động

⇒ Ta có hệ thức: Δt = NT’ = ( n ± 1)T

2. Ví dụ

Ví dụ 1: Một con lắc đơn A dao động trước mặt con lắc đồng hồ gõ giây B ( biết T’ = 2s). Thời gian giữa hai lần trùng phùng liên tiếp của con lắc B là 9 phút 50 giây. Tính chu kì T_A của con lắc A biết rằng chu kì cả nó lớn hơn 2 s một chút.

A. 2 s          B. 1,9932 s          C. 2,0068 s          D. 2,01 s

Hướng dẫn:

⇒ Ta có: Δt = 590s→ N_B = Δt/T_B = 590/2 = 295T_A>T_B

⇒ N_A = N_B −1 = 294

⇒ Δt = N_A .T_A = N_B .T_B

⇒ T_A = 590/294 = 2,0068s

Ví dụ 2: Cho con lắc đơn dao động trước mặt một con lắc của đồng hồ gõ giây (có chu kì dao động là 2s). Con lắc đơn dao động chậm hơn con lắc đồng hồ một chút nên có những hai lần con lắc đó chuyển động cùng chiều và đi qua vị trí cân bằng cùng một lúc ( gọi là những lần trùng phùng). Quan sát cho thấy hai lần trùng phùng kế tiếp cách nhau 9 phút 30 giây. Biết chiều dài của con lắc là l = 1m. Hãy xác định gia tốc rơi tự do g tại vị trí đặt của con lắc.

A. 9,874 m/s²          B. 9,811m/s²          C. 9,791m/s²          D. 9,654m/s²

Hướng dẫn:

Vì con lắc đơn dao động chậm hơn con lắc đồng hồ ( nghĩa là trong cùng một khoảng thời gian số dao động của nó nhỏ hơn số dao động của con lắc đồng hồ), cho nên trong khoảng thời gian Δt = 9 phút 30 giây

Vì T > 2 nên Δt = NT = (N + 1)T_o → N = Δt/T_o = ΔT/T – 1 → 1/T = 1/T_o – 1/Δt

→ T = 2,0068 s.

Gia tốc trọng trường tại nơi quan sát:

Ví dụ 3: Một con lắc lò xo và một con lắc đơn, khi ở dưới mặt đất cả hai con lắc này cùng dao động với chu kì T = 2s. Đưa cả hai con lắc lên đỉnh núi (coi là nhiệt độ không thay đổi) thì hai con lắc dao động lệch chu kì nhau. Thỉnh thoảng chúng lại cùng đi qua vị trí cân bằng và chuyển động về cùng một phía, thời gian giữa hai lần liên tiếp như vậy là 8 phút 20 giây. Tìm chu kì con lắc đơn tại đỉnh núi đó.

A. 2,010s.          B. 1,992s.          C. 2,008s.          D. 1,008 s.

Hướng dẫn:

Ta biết rằng chu kì dao động của con lắc lò xo phụ thuộc vào m và k chứ không phụ thuộc vào vị trí đặt con lắc, nên khi đưa con lắc từ mặt đất lên đỉnh núi thì chu kì dao động của con lắc lò xo không đổi và chỉ có con lắc đơn là thay đổi.

- Khi đưa con lắc đơn lên đỉnh núi thì chu kì dao động tăng, nghĩa là T > 2 s

- Δt = NT = (N+1)T_o → N = ΔtT = ΔtT_o – 1

→1/T = 1/T_o−1/Δt → T = 2,008s

→ Chọn C.