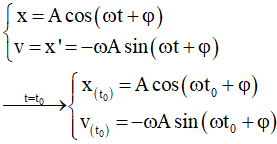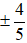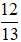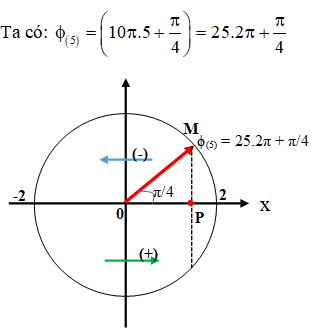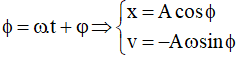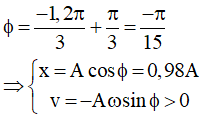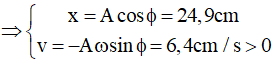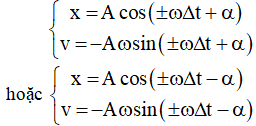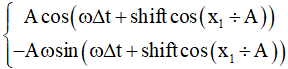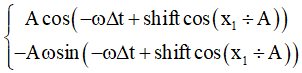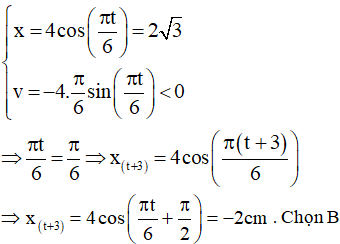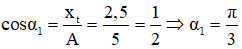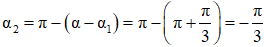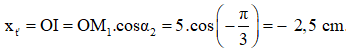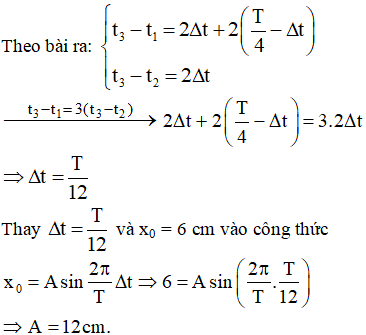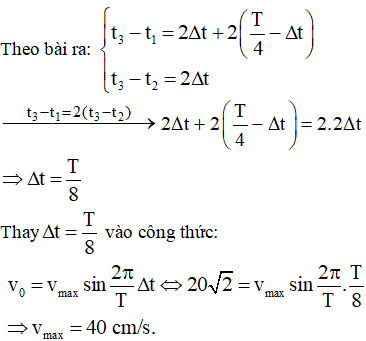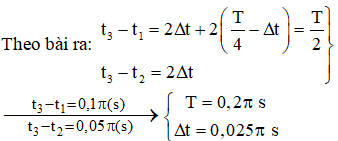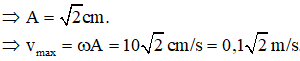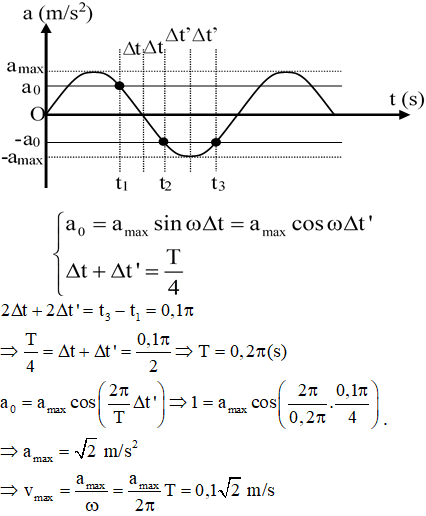Cách tìm li độ của vật tại thời điểm t hay, chi tiết

a) Tìm li độ và hướng chuyển động.

Vật chuyển động về vị trí cân bằng là nhanh dần (không đều) và chuyển động ra xa vị trí cân bằng là chậm dần (không đều).

Cách 1:

+ v(t₀) > 0: Vật đi theo chiều dương (x đang tăng).

+ v(t₀) < 0: Vật đi theo chiều âm (x đang giảm).

Cách 2:

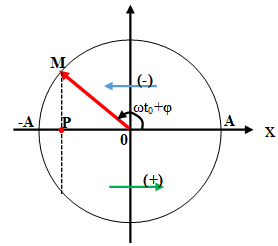
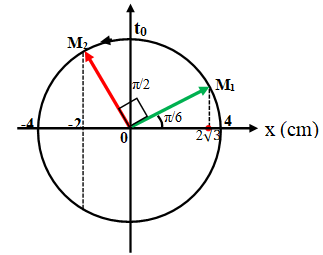
Xác định vị trí trên vòng lượng giác ở thời điểm t₀: ϕ = ωt₀ + φ.

Hạ M xuống trục Ox ta được vị trí của vật ở thời điểm t₀.

Nếu véctơ quay thuộc nửa trên vòng tròn lượng giác thì hình chiếu chuyển động theo chiều âm (li độ đang giảm).

Nếu véctơ quay thuộc nửa dưới vòng tròn lượng giác thì hình chiếu chuyển động theo chiều dương (li độ đang tăng).

Vậy li độ dao động điều hòa: x = A.cosϕ(t₀) = A.cos(ωt₀ + φ)

Vận tốc dao động điều hòa: v = x’ = -ωAsin ϕ(t₀) = - ωAsin(ωt₀ + φ).

Ví dụ 1: Một vật dao động điều hoà với phương trình x = 5cos(5πt + π/3)(cm). Biết ở thời điểm t có li độ là 3cm. Li độ dao động ở thời điểm sau đó 1/10(s) là:

A. 4cm.    B. 3cm.    C. -3cm.    D. 2cm

Hướng dẫn:

+ Ở thời điểm t: x = 5cos(5πt + π/3) = 3 cm

⇒ cos(5πt + π/3) = 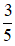 ⇒ sin(5πt + π/3) = 

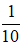
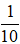
+ Ở thời điểm (t +  ): x = 5cos[5π(t +  ) + π/3] = 5cos(5πt + π/3 + π/2) = -5sin(5πt + π/3) = 4cm.

Chọn A

Ví dụ 2: Một vật dao động điều hòa với biên độ 13cm, t = 0 tại biên dương. Sau khoảng thời gian t (kể từ lúc ban đầu chuyển động) thì vật cách vị trí cân bằng O một đoạn 12cm. Sau khoảng thời gian 2t (kể từ t = 0) vật cách O một đoạn bằng x. Giá trị x gần giá trị nào nhất sau đây?

A. 9,35cm    B. 8,75cm

C. 6,15cm    D. 7,75cm

Hướng dẫn:

+ Phương trình dao động của vật là x = 13cosωt (cm).

+ Tại thời điểm t ta có: 12 = 13cosωt ⇒ cosωt = 

+ Tại thời điểm 2t ta có: x = 13cos²ωt = 13.[2cos²ωt –1] = 13.[2.(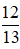 )2-1] = 9,15cm.

Chọn A

Ví dụ 3: Một vật doa động điều hòa có phương trình 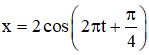 cm, trong đó t được tính bằng đơn vị giây (s). Lúc t = 5s vật chuyển động

A. nhanh dần theo chiều dương của trục Ox.

B. nhanh dần theo chiều âm của trục Ox.

C. chậm dần theo chiều dương của trục Ox.

D. chậm dần theo chiều âm của trục Ox.

Hướng dẫn:

Quan sát đường tròn lượng giác ta thấy vật đang chuyển động theo chiều âm về vị trí cân bằng (nhanh dần).

Chọn B

b) Tìm trạng thái quá khứ và tương lai đối với bài toán chưa cho biết phương trình của x, v, a, F...

Phương pháp chung:

Cách 1:

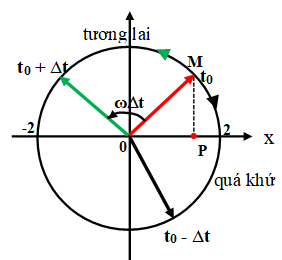
+ Dựa vào trạng thái ở thời điểm t₀ để xác định vị trí tương ứng trên vòng tròn lượng giác.

+ Để tìm trạng thái ở thời điểm quá khứ (t₀ – ∆t) ta quét 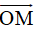 theo theo chiều âm của vòng tròn một góc ∆φ = ω.∆t.

+ Để tìm trạng thái ở thời điểm tương lai (t₀ + ∆t) ta quét 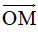 theo theo chiều dương của vòng tròn một góc ∆φ = ω.∆t.

Cách 2: Dùng phương trình lượng giác:

+ Chọn gốc thời gian t = t₀ = 0 và dùng vòng tròn lượng giác để viết pha dao động: ϕ = ωt + φ

+ Lần lượt thay t = -∆t và t = +∆t để tìm trạng thái quá khứ và tương lai:

Nếu v > 0: Vật đi theo chiều dương (x đang tăng).

Nếu v < 0: Vật đi theo chiều âm (x đang giảm).

Ví dụ 1: Một vật thực hiện dao động điều hòa với biên độ A, tại thời điểm t₁ = 1,2s vật đang ở vị trí x = A/2 theo chiều âm, tại thời điểm t₂ = 9,2s vật đang ở biên âm và đã đi qua vị trí cân bằng 3 lần tính từ thời điểm t₁. Hỏi tai thời điểm ban đầu thì vật đang ở đâu và đi theo chiều nào.

A. 0,98 chuyển động theo chiều âm.

B. 0,98A chuyển động theo chiều dương.

C. 0,588A chuyển động theo chiều âm.

D. 0,55A chuyển động theo chiều dương.

Hướng dẫn:

Cách 1:

Chọn lại gốc thời gian t = t₁ = 1,2s thì pha dao động có dạng: ϕ = ωt + π/3

Từ M₁ quay một vòng(ứng với thời gian T) thì vật qua vị trí cân bằng 2 lần, rồi lại trở về vị trí cũ, sau đó vật quay tiếp 1 góc 2π/3 (ứng với khoảng thời gian T/3) vật đến biên âm và tổng cộng đã đi qua VTCB 3 lần.

Do vậy: t₂ – t₁ = T + T/3 = 9,2 – 1,2 → T = 6s → ω = 2π/T = π/3.

Để tìm trạng thái ban đầu ta cho t = -1,2s thì ϕ = ωt + π/3

Chọn B

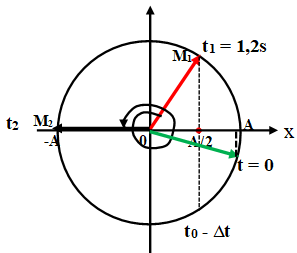
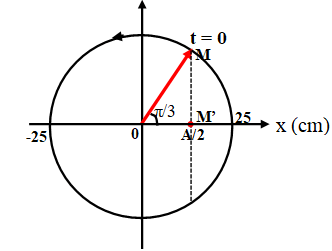
Cách 2: Ta xác định được vị trí của vật tại thời điểm t₁ = 1,2s trên vòng tròn lượng giác là ứng với điểm M₁.

Từ M₁ quay một vòng(ứng với thời gian T) thì vật qua vị trí cân bằng 2 lần, rồi lại trở về vị trí cũ, sau đó vật quay tiếp 1 góc 2π/3 (ứng với khoảng thời gian T/3) vật đến biên âm và tổng cộng đã đi qua VTCB 3 lần.

Do vậy: t₂ – t₁ = T + T/3 = 9,2 – 1,2 → T = 6s→ ω = 2π/T = π/3.

Để tìm trạng thái ban đầu ta cho M₁ quay theo chiều âm 1 góc:

∆φ = ω.∆t = π/3.1,2 = 0,4π (rad) = 72º

Khi đó, ta được vị trí ban đầu của vật có x = A.cos(0,4π-π/3) = 0,98A, và v > 0 (vecto quay khi đó nằm ở nữa dưới vòng tròn). Chọn B

Ví dụ 2: Một chất điểm chuyển động tròn đều với tốc độ 0,75 m/s trên đường tròn bán kính 0,25m. Hình chiếu M’ của điểm M lên đường kính của đường tròn dao động điều hòa. Biết tại thời điểm ban đầu, M’ đi qua vị trí x = A/2 theo chiều âm. Tại thời điểm t = 8s, M’ có tọa độ:

A. 24,9 cm đi theo chiều dương.

B. 24,9 cm đi theo chiều âm.

C. 22,6 cm đi theo chiều dương.

D. 22,6 cm đi theo chiều âm.

Hướng dẫn:

Biên độ và tần số góc: A = 25cm, ω = vT/A = 3 (rad/s)

→ Pha dao động: ϕ = 3t + π/3

Thay t = 8s thì ϕ = 3.8 + π/3 

Chọn A

Ví dụ 3: Một chất điểm chuyển động tròn đều với tốc độ 1 m/s trên đường tròn đường kính 0,5m. Hình chiếu M’ của điểm M lên đường kính của đường tròn dao động điều hòa. Biết tại thời điểm t – t₀, M’ đi qua vị trí qua vị trí cân bằng theo chiều âm. Hỏi trước thời điểm và sau thời điểm t₀ là 8,5s hình chiếu M’ ở ví trí nào và đi theo chiều nào?

Hướng dẫn:

Biên độ và tần số góc lần lượt là: A = 50/2 = 25cm; ω = vd/A = 100/25 = 4 (rad/s)

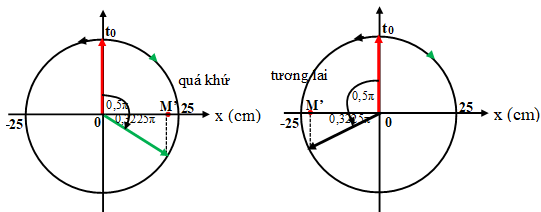
Góc cần quét: ∆φ = ω.∆t = 4.8,5 = 34 rad = 5.2π + 0,08225π.

+ Để tìm trạng thái ở thời điểm t = t₀ – 8,5s ta chỉ cần quét theo chiều âm 1 góc 0,8225π (rad):

x = 25.cos(0,8225π – π/2) = 13,2 > 0. Đồng thời ta thấy chất điểm nằm ở nữa dưới nên hình chiếu đi chiều dương.

+ Để tìm trạng thái ở thời điểm t = t₀ + 8,5s ta chỉ cần quét theo chiều dương 1 góc 0,8225π (rad):

x = 25.cos(0,8225π + π/2) = -13,2 < 0. Đồng thời ta thấy chất điểm nằm ở nữa dưới nên hình chiếu đi chiều dương.

c) Tìm trạng thái quá khứ và tương lai đối với bài toán cho biết phương trình của x, v, a, F...

Phương pháp chung: Biết tại thời điểm t vật có li độ x = x₁.

Cách 1: Giải bằng phương trình lượng giác (PTLG)

Từ phương trình dao động điều hòa x = Acos(ωt + φ) cho x = x₁.

Lấy nghiệm ωt + φ = α ứng với x đang giảm (vật chuyển động theo chiều âm vì v < 0) hoặc lấy nghiệm ωt + φ = -α ứng với x đang tăng (vật chuyển động theo chiều dương vì v > 0).

* Li độ và vận tốc dao động sau (trước) thời điểm đó ∆t giây là:

Dùng máy tính Casio 570ES, 570ESphus…ta có quy trình giải nhanh như sau:

* Li độ và vận tốc dao động sau thời điểm đó ∆t giây là:

* Li độ và vận tốc dao động trước thời điểm đó ∆t giây là:

Lưu ý: Lấy dấu cộng trước shiftcos(x₁ + A) nếu ở thời điểm t li độ đang giảm (theo chiều âm) và lấy dấu trừ (-) nếu ở thời điểm t li độ đang tăng (theo chiều dương).

Cách 2: Dùng vòng tròn lượng giác (VTLG)

+ Dánh dấu vị trí x₀ trên trục Ox. Kẻ đoạn thẳng vuông góc Ox, cắt đường tròn tại hai điểm. căn cứ vào chiều chuyển động để chọn vị trí M duy nhất trên đường tròn.

+ Vẽ bán kính OM. Trong khoảng thời gian ∆t, góc ở tâm mà OM quét được là α = ω.∆t > 0.

+ Vẽ OM’ lệch với OM một góc α, từ M’ hạ đường vuông góc với Ox cắt ở đâu thì đó là li độ cần xác định.

Ví dụ 1: Một vật dao động điều hòa theo phương trình x = 4cos(πt/6) cm (t tính bằng giây). Tại thời điểm t₁ li độ của vật là 2√3 cm và đang giảm. Tính li độ sau thời điểm t₁ là 3s

A. -2,5cm.    B. -2cm.    C. 2cm.    D. 3cm.

Hướng dẫn:

Cách 1: Dùng phương trình lượng giác.

Bấm máy tính: Chọn đơn vị góc trong máy tính là rad.

Bấm nhẩm: 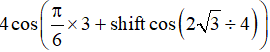 rồi bấm = sẽ được -2. Chọn B.

Cách 2. Dùng VTLG

Tại thời điểm t₁ có li độ là 2√3 cm và đnag giảm nên chất điểm chuyển động tròn đều trên vòng tròn nằm tai M₁.

+ Để tìm trạng thái ở thời điểm t = t₁ + 3s ta quét theo chiều dương góc: ∆ϕ = ω∆t + π/2 và lúc này chuyển động tròn đều tại M₂. Điểm M₂ nằm ở nửa trên vòng tròn nên hình chiếu của nó đi theo chiều âm (x đang giảm).

Li độ của dao động lúc này là: 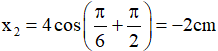 . Chọn B

Ví dụ 2: Một chất điểm dao động theo trục Ox có phương trình dao động là 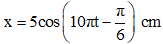 . Tại thời điểm t vật có li độ x = 2,5 cm và đang có xu hướng tăng, thì tại thời điểm t’ = t + 0,1 s vật có li độ là:

A. 5 cm    B. 2,5 cm    C. – 5 cm    D. – 2,5 cm

Hướng dẫn:

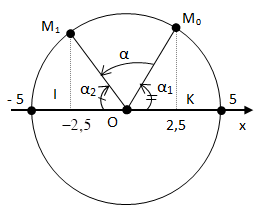
Tại thời điểm t do vật đang ở vị trí x = 2,5 cm và đang có xu hướng tăng nên vật sẽ đi cùng với chiều dương của trục tọa độ. Khi đó, vật quét 1 góc ở tâm là α1:

Sau thời gian t’ = t + 0,1 vật sẽ quét thêm 1 góc α như hình vẽ.

Khi đó: α = ω∆t = 10π.0,1 = π

Suy ra: 

Xét tam giác vuông OIM₁ ta có:

Chọn D

d) Li độ, vận tốc, gia tốc, … tại 3 thời điểm t₁, t₂, t₃

Các đại lượng li độ, vận tốc, gia tốc, động lượng và lực kéo về biến thiên điều hòa cùng tần số

Một đại lượng x biến thiên điều hòa với biên độ A thì phân bố thời gian trên trục và trên vòng tròn lượng giác như sau:

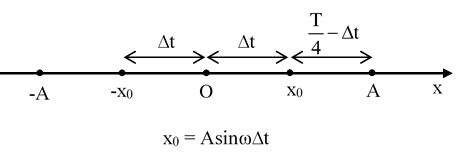
Đối với dạng bài toán cho hệ thức liên hệ giữa t₁, t₂, t₃ với nhau và thỏa mãn điều kiện về li độ x, gia tốc a và vận tốc v ta thường làm theo các bước sau:

+ Xác định li độ (vận, tốc, gia tốc) và chiều chuyển động của chất điểm tại các thời điểm t₁, t₂, t₃. Lưu ý bước này rất quan trọng trong quá trình giải dạng bài toán này.

+ Dựa vào giả thuyết bài toán vẽ thật chính xác sơ đồ thời gian.

+ Dựa vào các hệ thức liên hệ và sơ đồ thời gian để xác định các đại lượng mà bài toán yêu cầu.

Ví dụ 1: Một vật dao động điều hòa mà 3 thời điểm liên tiếp t₁, t₂, t₃ với t₃ – t₁ = 3(t₃ –t₂), li độ thỏa mãn x₁ = x₂ = – x₃ = 6 cm. Biên độ dao động của vật là

A. 12 cm.    B. 8 cm.    C. 16 cm.    D. 10 cm.

Hướng dẫn:

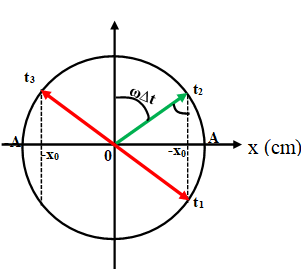
Không làm mất tính tổng quát có thể xem ở thời điểm t₁ vật có li độ x₀ và đang tăng, đến thời điểm t₂ vật có li độ x₀ và đang giảm, đến thời điểm t₃ vật có li độ – x₀ và đang giảm.

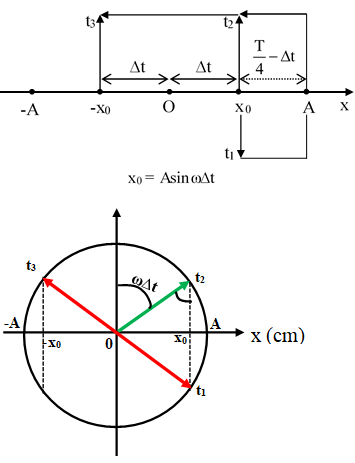
Chọn đáp án A

Ví dụ 2: Một dao động điều hòa mà 3 thời điểm liên tiếp t₁, t₂, t₃ với t₃ – t₁ = 2(t₃ –t₂), vận tốc có cùng độ lớn là 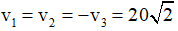 cm/s. Vật có vận tốc cực đại là

A. 28,28 cm/s.    B. 40 cm/s.

C. 32,66 cm/s.    D. 56,57 cm/s.

Hướng dẫn:

Không làm mất tính tổng quát có thể xem ở thời điểm t₁ vật có vận tốc v₀ và đang tăng, đến thời điểm t₂ vật có vận tốc v₀ và đang giảm, đến thời điểm t₃ vật có vận tốc – v₀ và đang giảm.

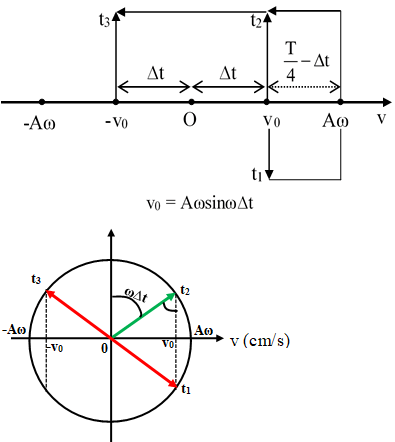
Chọn đáp án B

Ví dụ 3: Một chất điểm dao động điều hòa, ba thời điểm liên tiếp t₁, t₂, t₃ có gia tốc lần lượt là a₁, a₂, a₃. Biết t₃ – t₁ = 2(t₃ – t₂) = 0,1π s; a₁ = – a₂ = – a₃ = 1 m/s². Tính tốc độ cực đại của dao động điều hòa.

Hướng dẫn:

Cách 1: Không làm mất tính tổng quát có thể xem ở thời điểm t₁ vật có gia tốc a₀ và đang giảm, đến thời điểm t₂ vật có gia tốc - a₀ và đang giảm, đến thời điểm t₃ vật có gia tốc - a₀ và đang tăng.

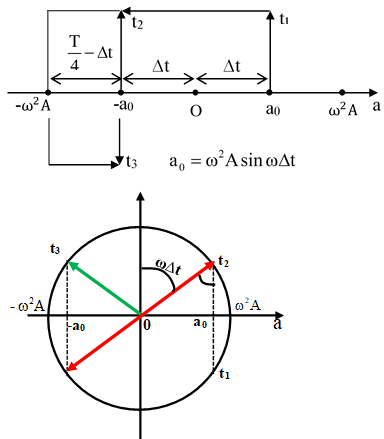
a₀ = ω²Asinω∆t

Chọn đáp án A

Cách 2: Dựa vào đồ thị gia tốc theo thời gian:

Chọn đáp án A