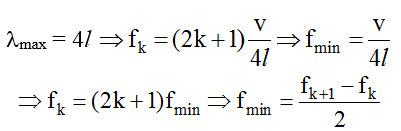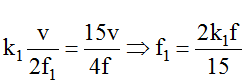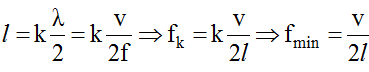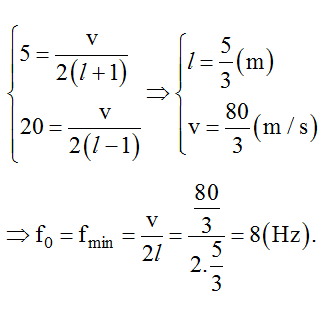Cách tìm điều kiện để có sóng dừng, tìm số nút, số bụng trên dây đang có sóng dừng

A. Phương pháp giải

1. Điều kiện có sóng dừng trên một sợi dây dài l

* Khi hai đầu cố định thì chiều dài dây phải thỏa mãn: l = kλ/2 ( k ∈ N*)

+ Số bụng sóng = số bó sóng = k

Số nút sóng = k + 1

* Khi một đầu cố định, một đầu tự do thì chiều dài dây phải thỏa mãn: l = (2k+1) λ/4 ( k ∈ N)

+ Số bó sóng nguyên = k

Số bụng sóng = số nút sóng = k + 1

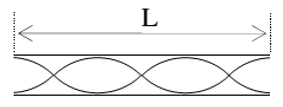
* Trường hợp sóng dừng với 2 đầu tự do (2 đầu đều là bụng sóng): Đây là trường hợp xảy ra trong ống sáo có chiều dài L hở 2 đầu và có âm phát ra cực đại.

+ Chiều dài dây: l = kλ/2 ( k ∈ N*)

+ Số bụng sóng = k +1; số bó sóng = k -1;

số nút sóng = k.

2. Số nút, số bụng giữa 2 điểm M, N bất kì trên dây đang có sóng dừng

* Nếu tại M là nút, còn N không phải nút hoặc bụng thì phân tích: MN = kλ/2 + ∆x

Sau đó so sánh ∆x với λ/4

+ Nếu ∆x > λ/4 thì số nút = số bụng = k + 1.

+ Nếu ∆x < λ/4 thì số nút = k + 1, số bụng = k.

* Nếu tại M là bụng, còn N không phải nút hoặc bụng thì phân tích: MN = kλ/2 + kλ/4 + ∆x

Sau đó so sánh ∆x với λ/4.

+ Nếu ∆x > λ/4 thì số nút = số bụng = k + 1.

+ Nếu ∆x < λ/4 thì số nút = k, số bụng = k + 1.

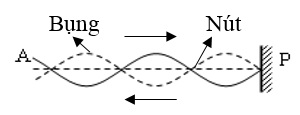
* Nếu một đầu dây được gắn với âm thoa để tạo sóng dừng thì đầu dây đó luôn là nút sóng, việc xác định tính chất của hai đầu dây chủ yếu là xác định được đầu còn lại là nút hay bụng. Nếu đề bài cho đầu còn lại cố định thì nó là bụng, còn nếu đầu còn lại lơ lửng thì đó là bụng sóng.

* Từ các điều kiện về chiều dài và tần số ta có chiều dài nhỏ nhất hay tần số nhỏ nhất để có sóng dừng là:

+ Trường hợp sóng dừng với hai đầu nút (vận cản cố định) và trường hợp sóng dừng với 2 đầu tự do.

λ_max/ = 2l => f_k = k v/2l => f_min = v/2l

=> f_k = kf_min => f_min = f_k+1 - f_k

(tần số gây ra sóng dừng bằng bội số nguyên lần tần số nhỏ nhất gây ra sóng dừng)

Trường hợp sóng dừng với một đầu là nút B (cố định), một đầu là bụng A (tự do):

(tần số gây ra sóng dừng bằng bội số nguyên lẻ lần tần số nhỏ nhất gây ra sóng dừng)

3. Một số chú ý

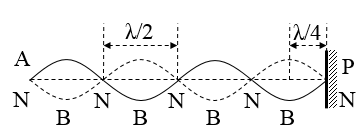
+ Khoảng cách gần nhất giữa hai bụng sóng là λ/2. Khoảng cách gần nhất giữa hai nút sóng là λ/2.

+ Khoảng cách gần nhất giữa nút sóng và bụng sóng là λ/4.

+ Đầu cố định hoặc đầu dao động nhỏ là nút sóng. Đầu tự do là bụng sóng

+ Hai điểm đối xứng với nhau qua nút sóng luôn dao động ngược pha. Hai điểm đối xứng với nhau qua bụng sóng luôn dao động cùng pha.

+ Các điểm trên dây đều dao động với biên độ không đổi  năng lượng không truyền đi.

+ Khoảng thời gian giữa hai lần sợi dây căng ngang (các phần tử đi qua VTCB) là T/2.

=> Khoảng thời gian giữa n lần liên tiếp sợi dây duỗi thẳng là:

+ Sóng dừng được tạo bởi sự rung của nam châm điện với tần số dòng điện f thì tần số sóng là 2f.

+ Khi cho dòng điện có tần số f chạy trong dây kim loại, dây kim loại được đặt giữa 2 cực của nam châm thì sóng dừng trên dây sẽ có tần số là f.

B. Ví dụ minh họa

Ví dụ 1: Một sợi dây AB dài 100cm căng ngang, đầu B cố định, đầu A gắn với một nhánh của âm thoa dao động điều hòa với tần số 40Hz. Trên dây AB có một sóng dừng ổn định, A được coi là nút sóng. Tốc độ truyền sóng trên dây là 20m/s. Kể cả A và B, trên dây có:

A. 5 nút và 4 bụng    B. 3 nút và 2 bụng

C. 9 nút và 8 bụng    D. 7 nút và 6 bụng

Hướng dẫn giải:

Chọn A

Bước sóng của hai nguồn: λ = v/f = 20/40 = 0,5m = 50cm.

Số bụng sóng trên dây:

Do hai đầu A và B của sợi dây cố định nên: l = kλ/2 (với k là số bụng sóng)

=> k = 2l/λ = 2.100/50 = 4

Số nút sóng trên dây: Số nút = Số bụng + 1 = 4 + 1 = 5 (nút)

Ví dụ 2: Một dây đàn dài 0,6 m, hai đầu cố định dao động với tần số 50 Hz, có một bụng ở giữa dây.

a) Tính bước sóng và tốc độ truyền sóng.

b) Nếu dây dao động với 3 bụng thì bước sóng là bao nhiêu?

Hướng dẫn giải:

a) Dây dao động với một bụng, ta có l = λ/2 . Suy ra λ = 2l =2.0,6 = 1,2 m.

Tốc độ truyền sóng: v = λ.f = 1,2.50 = 60 m/s.

b) Khi dây dao động với 3 bụng ta có: l = 3λ'/2 => λ' = 2l/3 = 0,4m.

Ví dụ 3: Một sợi dây căng giữa hai điểm cố định cách nhau 75cm. Người ta tạo sóng dừng trên dây. Hai tần số gần nhau nhất cùng tạo ra sóng dừng trên dây là 150Hz và 200Hz. Vận tốc truyền sóng trên dây đó bằng:

A. 7,5m/s    B. 300m/s    C. 225m/s     D. 75m/s

Hướng dẫn giải:

Chọn D

Sóng dừng hai đầu cố định: l = kλ/2 = k v/2f => f = k v/2l.

Hai tần số gần nhau nhất tạo sóng dừng nên f₁ = k v/2l = 150 Hz và f₂ = (k+1) v/2l = 200 Hz .

Trừ vế theo vế ta có:

(k+1) v/2l - k v/2l = 200 - 150 = 50 => v/2l = 50 => v = 100l = 75 m/2

Ví dụ 4: Dây AB = 90cm có đầu A cố định, đầu B tự do. Khi tần số trên dây là 10Hz thì trên dây có 8 nút sóng dừng.

a. Tính khoảng cách từ A đến nút thứ 7

A. 0,84m.    B. 0,72m.    C. 1,68m.    D. 0,80m.

b. Nếu B cố định và tốc độ truyền sóng không đổi mà muốn có sóng dừng trên dây thì phải thay đổi tần số f một lượng nhỏ nhất bằng bao nhiêu?

A. 1/3Hz.    B. 2/3Hz.    C. 10,67 Hz.    D. 10,33 Hz.

Hướng dẫn giải:

a) Chọn B    b) Chọn B

a) Ta có điều kiện có sóng dừng: AB = (k+0,5) λ/2

Trên dây có 8 nút sóng => k = 7 => λ = 24cm.

Nút thứ 7 là D: AD = ; từ A đến D có 7 nút => k’ = 6 => AD = 0,72m.

b. Khi B cố định thì điều kiện có sóng dừng: AB = k₁. λ₁/2 = k₁. v/2f₁ (1)

Khi B tự do: AB = (k +0,5)λ/2 = (7 + 0,5)v/2f (2)

Từ (1) và (2), ta có:

Độ thay đổi tần số: ∆f = f - f₁ = ( 1- 2k₁f/15)f.

Để Δf_min thì k_max = 7 => Δf_min= 2/3 Hz.

Ví dụ 5: Một sợi dây đàn hồi hai đầu cố định. Tần số dao động bé nhất để sợi dây có sóng dừng là f_o. Tăng chiều dài thêm 1 m thì tần số dao động bé nhất để sợi dây có sóng dừng là 5 Hz. Giảm chiều dài bớt 1 m thì tần số dao động bé nhất để sợi dây có sóng dừng là 20 Hz. Giá trị của f_o là

A. 4 Hz.     B. 7 Hz.     C. 9 Hz.     D. 8 Hz.

Hướng dẫn giải:

Vì sợi dây hai đầu cố định nên điều kiện sóng dừng là:

Áp dụng công thức này cho hai trường hợp: