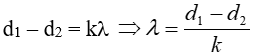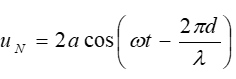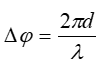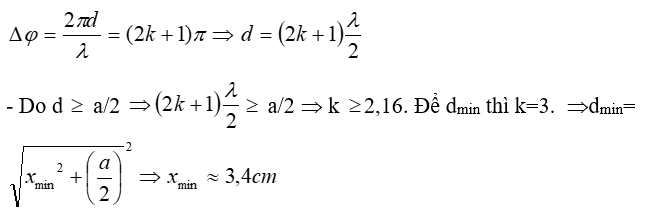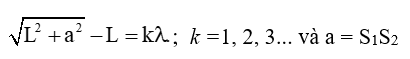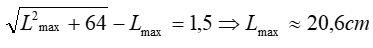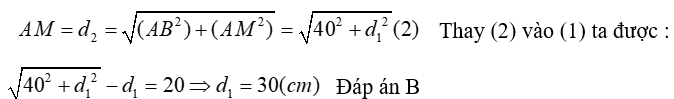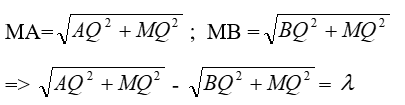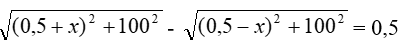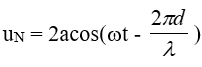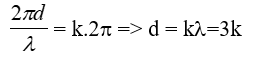Cách giải bài tập Điểm M có tính chất đặc biệt trong Giao thoa sóng hay, chi tiết

1. Phương pháp

Sử dụng các điều kiện cực đại, cực tiểu trong giao thoa sóng và áp dụng kiến thức hình học để giải quyết bài toán dạng này.

2. Ví dụ

Ví dụ 1: Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn kết hợp S₁, S₂ cách nhau 8cm dao động cùng pha với tần số f = 20Hz. Tại điểm M trên mặt nước cách S₁, S₂ lần lượt những khoảng d₁ = 25cm, d₂ = 20,5cm dao động với biên độ cực đại, giữa M và đường trung trực của AB có hai dãy cực đại khác.

a. Tính tốc độ truyền sóng trên mặt nước.

b. N là một điểm thuộc đường trung trực của đoạn thẳng S₁S₂ dao động ngược pha với hai nguồn. Tìm khoảng cách nhỏ nhất từ N đến đoạn thẳng nối S₁S₂.

c. Điểm C cách S₁ khoảng L thỏa mãn CS₁ vuông góc với S₁S₂. Tính giá trị cực đại của L để điểm C dao động với biên độ cực đại.

Hướng dẫn:

a. Tính tốc độ truyền sóng:

- Tại M sóng có biên độ cực nên: 

- Giữa M và trung trực của AB có hai dãy cực đại khác ⇒ k = 3

- Từ đó ⇒ λ = 1,5 cm , vận tốc truyền sóng: v = λf = 30 cm/s

b. Tìm vị trí điểm N

- Giả sử u₁ = u₂ = acosωt, phương trình sóng tại N:

- Độ lệch pha giữa phương trình sóng tại N và tại nguồn: 

-Để dao động tại N ngược pha với dao động tại nguồn thì :

c. Xác định L_max

- Để tại C có cực đại giao thoa thì: 

- Khi L càng lớn đường CS1 cắt các cực đại giao thoa có bậc càng nhỏ (k càng bé), vậy ứng với giá trị lớn nhất của L để tại C có cực đại là k =1

- Thay các giá trị đã cho vào biểu thức trên ta nhận được:

Ví dụ 2: Trên bề mặt chất lỏng có hai nguồn kết hợp AB cách nhau 40cm dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số f=10(Hz), vận tốc truyền sóng 2(m/s). Gọi M là một điểm nằm trên đường vuông góc với AB tại đó A dao động với biên độ cực đại. Đoạn AM có giá trị lớn nhất là :

A. 20cm          B. 30cm          C. 40cm          D.50cm

Hướng dẫn:

Ta có λ = v/f = 200/10 = 20(cm)

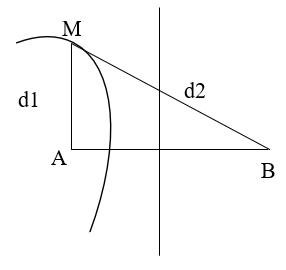
Do M là một cực đại giao thoa nên để đoạn AM có giá trị lớn nhất thì M phải nằm trên vân cực đại bậc 1 như hình vẽ và thỏa mãn :

d₂ - d₁ = kλ = 1. 20 = 20(cm) (1). ( do lấy k= +1)

Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có :

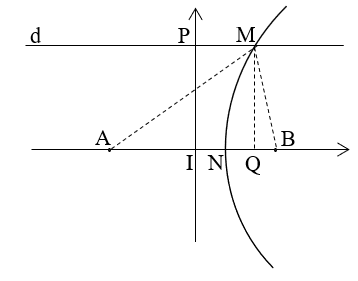
Ví dụ 3: Hai nguồn sóng AB cách nhau 1m dao động cùng pha với bước sóng 0,5m. I là trung điểm AB. P là điểm nằm trên đường trung trực của AB cách I 100m. Gọi d là đường thẳng qua P và song song với AB. Tìm điểm M thuộc d và gần P nhất, dao động với biên độ cực đại. (Tìm khoảng cách MP)

Hướng dẫn:

Vì A và B cùng pha và M gần P nhất và dao động với biên độ cực đại nên M thuộc cực đại ứng với k =1

Ta có: MA – MB = k.λ = λ ; Theo hình vẽ Ta có:

Đặt MP = IQ = x, có PI = MQ = 100m

Ta có: 

Giải phương trình tìm được x = 57,73m

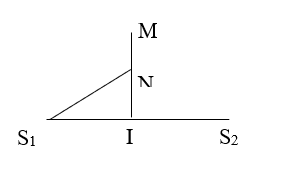
Ví dụ 4: Thực hiện giao sóng cơ trên mạch nước với hai nguồn S₁;S₂ cánh nhau 12 cm, biết bước sóng của sóng trên mặt nước là λ = 3cm. Trên đường trung trực của hai nguồn có 1 điểm M, M cách trung điểm I của hai nguồn 8cm. Hỏi trên MI có bao nhiêu nhiêu điểm dao động cùng pha với 2 nguồn?

A:4 điểm          B:2 điểm          C: 6 điểm          D:3 điểm

Hướng dẫn:

Giả sử phương trình sóng ở hai nguôn: u = acosωt.

Xét điểm N trên MI: S₁N = S₂N = d.

IN = x Với 0 ≤ x ≤ 8 (cm)

Biểu thức sóng tại N: 

Để u_N dao động cùng pha với hai nguồn:

d² = SI² + x² = 6² + x² ⇒ 9k² = 36 + x² ⇒ 0 ≤ x² = 9k² – 36 ≤ 64

6 ≤ 3k ≤ 10 ⇒ 2 ≤ k ≤ 3.

Có hai giá trị của k: k = 2; x = 0 (N ≡ I) và k = 3 ; x = 3√5 (cm) Chọn B.