Cách tìm quãng đường, quãng đường lớn nhất, nhỏ nhất (smax, smin) vật đi được hay, chi tiết
Với Cách tìm quãng đường, quãng đường lớn nhất, nhỏ nhất (smax, smin) vật đi được hay, chi tiết Vật lý lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách tìm quãng đường, quãng đường lớn nhất, nhỏ nhất (smax, smin) vật đi được hay, chi tiết
Cách tìm quãng đường, quãng đường lớn nhất, nhỏ nhất (smax, smin) vật đi được hay, chi tiết
1. Phương pháp
a) Loại 1: Bài toán xác định quãng đường vật đi được trong khoảng thời gian Δt.
Chú ý:
+ Trong thời gian t = 1T vật đi được quãng đường S = 4A
+ Trong thời gian nửa chu kỳ T vật đi được quãng đường S = 2A
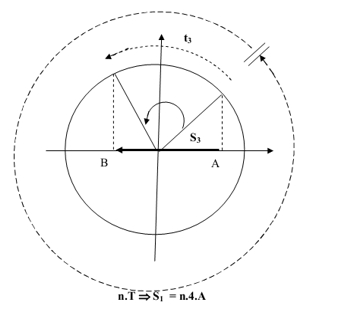
Bước 1: Xác định vị trí hoặc thời điểm t1, t2 cho trước trên đường tròn. Tìm Δt, Δt = t2 - t1.
Bước 2: Tách Δt = n.T + t* ⇔ Δφ = n.vong + φ*
Bước 3: Tìm quãng đường. S = n.4.A + S*.
Căn cứ vào vị trí và chiều chuyển động của vật tại t1 và t2 để tìm ra S3
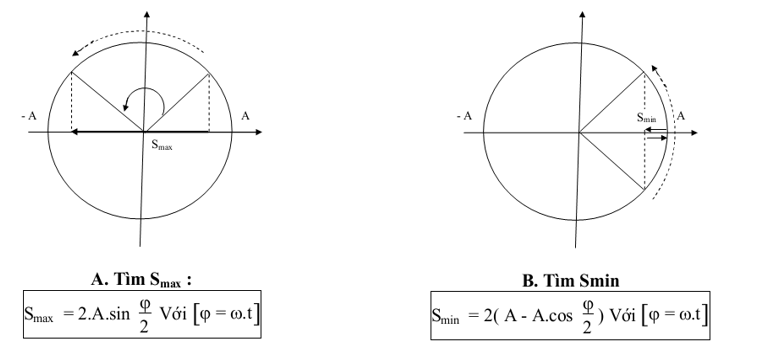
b) Loại 2: Bài toán xác định Smax - Smin vật đi được trong khoảng thời gian Δt (Δt < T/2 )
Nhận xét:
+ Quãng đường max đối xứng qua VTCB
+ Quãng đường min thì đối xứng qua biên
BẢNG TÍNH NHANH CÁC GIÁ TRỊ CỰC ĐẠI – CỰC TIỂU CỦA QUÃNG ĐƯỜNG
| Δt | T/6 | T/4 | T/3 | T/2 | 2T/3 | 3T/4 | 5T/6 | T |
| Smax | A | A√2 | A√3 | 2A | 2A + A | 2A + A√2 | 2A + A√3 | 4A |
| Smin | 2A - A√3 | 2A - A√2 | A | 2A | 4A - A√3 | 4A - A√2 | 3A | 4A |

2. Ví dụ
Ví dụ 1: Một vật dao động điều hòa với phương trình x = 6cos(4πt + π/3) cm. Tính quãng đường vật đi được sau 1 s kể từ thời điểm ban đầu.
A. 24 cm B. 60 cm C. 48 cm D. 64 cm
Hướng dẫn:
Ta có: T = 2π/ ω = 0,5s ⇒ Δt/T = 1/0,5 = 2
⇒ Δt = 2T
⇒ S = 2. 4A = 48cm
Ví dụ 2: Một vật dao động điều hòa với phương trình x = 6cos(4πt + π/3) cm. Tính quãng đường vật đi được sau 2,125 s kể từ thời điểm ban đầu?
A. 104 cm B. 104,78cm C. 104,2cm D. 100 cm
Hướng dẫn:
Ta có: T = 2π/ω = 0,5s ⇒ Δt/T = 2,125/0,5 = 4,25
⇒ Δt = 4T + T/4
⇔ Δφ = 4.vong + 90ο
⇒ S = 4. 4A + s*
Tính s*:
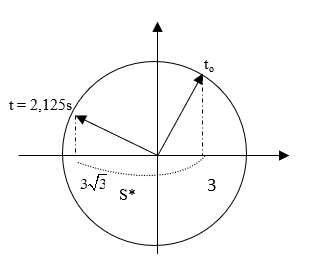
Xác định điểm xuất phát và chiều chuyển động
t = 0 ⇒ x = A/2 và vật đi theo chiều (-) vì φ > 0
Dùng đường tròn để biểu diễn đoạn đường đi của vật hết thời gian T/4 ⇔ 30ο + 60ο
s* = A/2 + A√3/2 = 3 + 3√2 = 8,2 cm
⇒ 16.6 + 8,2 = 104,2 cm
Ví dụ 3: Vật dao động điều hòa với phương trình x = 5cos(4πt + π/6) cm. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian
A. 5 cm B. 5 cm C. 5 cm D. 10 cm
Hướng dẫn:
Sử dụng công thức tính Smax