Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 4
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 10 Bài tập cuối chương 4 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài tập cuối chương 4. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài tập cuối chương 4
Bài tập
Lời giải:
Áp dụng định lí côsin ta có:
c2 = a2 + b2 - 2ab.cos C = 492 + 26,42 - 2 . 49 . 26,4 . cos ≈ 1 344,53
c ≈ 36,67
Áp dụng hệ quả của định lí côsin ta có:
cos A = ≈ -0,19.
≈ 101o.
Khi đó ≈ 31o40’.
Bài 2 trang 78 Toán lớp 10 Tập 1: Cho tam giác ABC. Biết a = 24, b = 13, c = 15. Tính các góc .
Lời giải:
Áp dụng hệ quả của định lí côsin ta có:
Áp dụng định lí sin ta có:
Bài 3 trang 78 Toán lớp 10 Tập 1: Cho tam giác ABC có a = 8, b = 10, c = 13.
a) Tam giác ABC có góc tù không?
b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.
c) Lấy điểm D đối xứng với A qua C. Tính độ dài BD.
Lời giải:
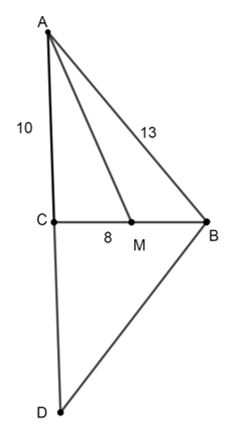
a) Áp dụng định lí côsin ta có:
Vậy tam giác ABC có góc là góc tù.
b) Vì M là trung điểm của CB (vì AM là đường trung tuyến ) nên
CM = MB = 8 : 2 = 4 cm
Áp dụng định lí côsin ta có:
Ta có:
Vì D đối xứng với A qua C nên
Áp dụng định lí côsin ta có:
Bài 4 trang 79 Toán lớp 10 Tập 1: Cho tam giác ABC có , b = 8, c = 5. Tính:
c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.
Lời giải:
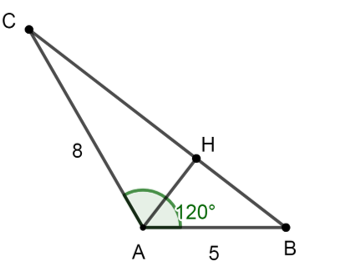
a) Áp dụng định lí côsin ta có:
Áp dụng định lí sin ta có:
b)
c) Ta có:
Xét tam giác AHB vuông tại H ta có:
Bài 5 trang 79 Toán lớp 10 Tập 1: Cho hình bình hành ABCD.
a) Chứng minh 2(AB2 + BC2) = AC2 + BD2.
b) Cho AB = 4, BC = 5, BD = 7. Tính AC.
Lời giải:
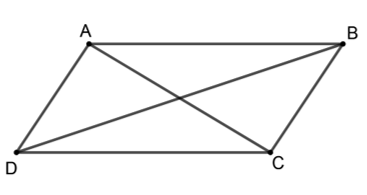
a) Áp dụng định lí côsin ta có:(1)
Mà theo tính chất của hình bình hành : CB = AD và (Vì AD//BC và là hai góc trong cùng phía)
(2)
Cộng (1) và (2) vế theo vế ta được:
(đpcm)
b) Áp dụng kết quả đã chứng minh được ở câu a) ta được:
Bài 6 trang 79 Toán lớp 10 Tập 1: Cho tam giác ABC có a = 15, b = 20, c = 25.
a) Tính diện tích tam giác ABC.
b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Lời giải:
a) Ta có:
Áp dụng công thức Heron:
b)
Bài 7 trang 79 Toán lớp 10 Tập 1: Cho tam giác ABC. Chứng minh rằng:
Lời giải:
Ta có: cotA + cot B + cot C
Mà áp dụng hệ quả của định lí côsin ta có:
(1)
Ta có: (2)
Kết hợp (1) và (2) ta được:
(đpcm)
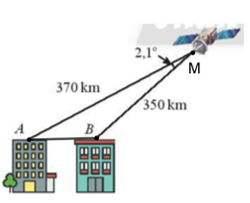
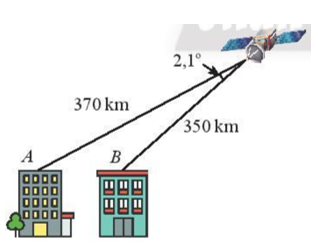
Gọi vị trí của máy bay là điểm M
Áp dụng định lí côsin ta có:
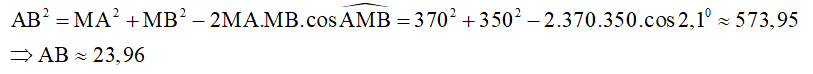
Vậy khoảng cách giữa 2 nóc toà cao ốc khoảng 23,96 km
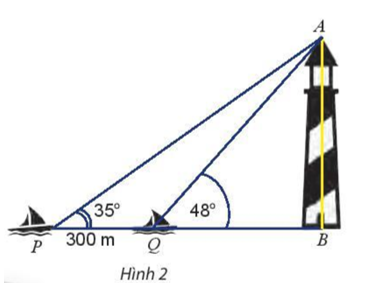
Ta có:
Trong tam giác APQ có:
Áp dụng định lí sin ta có:
m
Xét tam giác ABQ vuông tại B ta có: m.
Vậy chiều cao của tháp hải đăng khoảng 568,45 m.
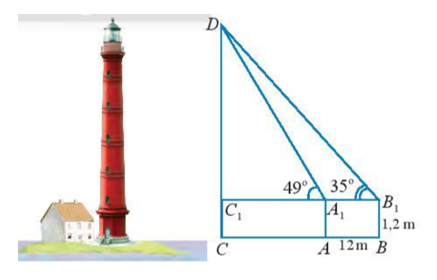
Ta có:
Xét tam giác có:
Áp dụng định lí sin ta có:
Xét tam giác vuông tại ta có:
Ta có: CD = 21,47 + 1,2 = 22,67 m.
Vậy chiều cao của tháp khoảng 22,67 m.
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo với cuộc sống hay, chi tiết khác:
Giải Toán 10 Bài 2: Định lí côsin và định lí sin - Chân trời sáng tạo
Giải Toán 10 Bài 3: Giải tam giác và ứng dụng thực tế - Chân trời sáng tạo
Giải Toán 10 Bài 1: Khái niệm vectơ - Chân trời sáng tạo
Giải Toán 10 Bài 2: Tổng và hiệu của hai vectơ - Chân trời sáng tạo
Giải Toán 10 Bài 3: Tích của một số với một vectơ - Chân trời sáng tạo