Giải bài tập Toán 10 Bài tập cuối chương 2

Video giải bài tập Toán 10 Bài tập cuối chương 2

Bài tập

Bài 1 trang 39 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ Oxy.

a) -2x + y - 1 ≤ 0;

b) -x + 2y > 0;

c) x – 5y < 2

d) -3x + y + 2 ≤ 0;

e) 3(x – 1) + 4(y – 2 ) < 5x – 3.

Lời giải:

a) –2x + y – 1 ≤ 0           

Vẽ đường thẳng d: –2x + y – 1 =  0 qua hai điểm (0; 1) và (–1; –1)

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ d và –2.0 + 0 – 1 = –1 < 0 . Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không gạch chéo).

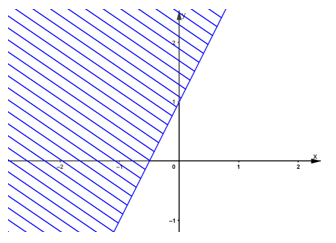
b) –x + 2y > 0

Vẽ đường thẳng d: –x + 2y = 0 đi qua hai điểm (0; 0) và (2; 1)

Xét điểm A(1; 1) ta thấy: A ∉ d và –1 + 2.1 = 1 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm A (không kể bờ d) (miền không gạch chéo).

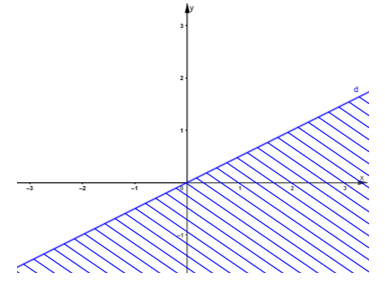
c) x – 5y < 2 ⇔ x – 5y – 2 < 0 

Vẽ đường thẳng d: x – 5y – 2 = 0  qua hai điểm (2; 0) và (7; 1).

Xét điểm O(0; 0) ta thấy: O ∉ d và 0 – 5.0 – 2 = -2  < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không gạch chéo).

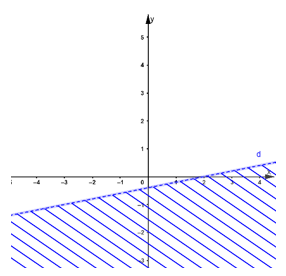
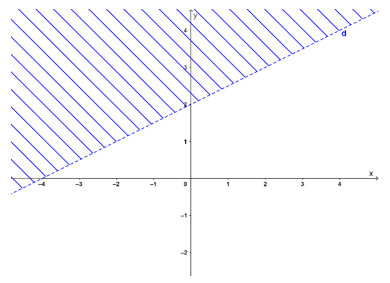
d) –3x + y + 2 ≤ 0

Vẽ đường thẳng d: –3x + y + 2 = 0 qua hai điểm (0; - 2); (1; 1).

Xét điểm O(0; 0) ta thấy: O ∉ d và –3.0 + 0 + 2 = 2 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm O (không kể bờ d) (miền không gạch chéo).

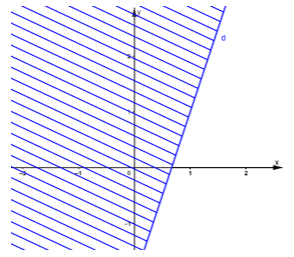
e) 3(x – 1) + 4. ( y – 2)  < 5x – 3

⇔ 3x – 3 +4y – 8 – 5x + 3 < 0

⇔ – 2x + 4y – 8 < 0

⇔ – x + 2y – 4 < 0

Vẽ đường thẳng d: – x + 2y – 4 = 0 qua hai điểm (0;  2) và (-2; 1)

Xét điểm O(0; 0) ta thấy: O ∉ d và –0 + 2.0 – 4 = –4 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không gạch chéo).

Bài 2 trang 39 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy.

$\left\{\begin{array}{c}x-2y>0\\ x+3y<3.\end{array}\right.$

Lời giải:

- Vẽ đường thẳng x – 2y = 0 qua hai điểm (0; 0) và (2; 1)

Xét điểm A(1; 1) ta thấy: A không thuộc đường thẳng x – 2y = 0  và 1 – 2.1 = -1  < 0. Do đó, miền nghiệm của bất phương trình x - 2y > 0 là nửa mặt phẳng không chứa điểm A và không kể đường thẳng x – 2y = 0 (miền không gạch chéo).

- Vẽ đường thẳng x + 3y = 3 qua hai điểm (0; 1) và (3; 0)

Xét điểm O(0; 0) ta thấy: O không thuộc đường thẳng x + 3y = 3 và 0 + 3.0 – 3 = -3 < 0. Do đó, miền nghiệm của bất phương trình x + 3y < 3 là nửa mặt phẳng chứa điểm O (miền không gạch chéo).

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

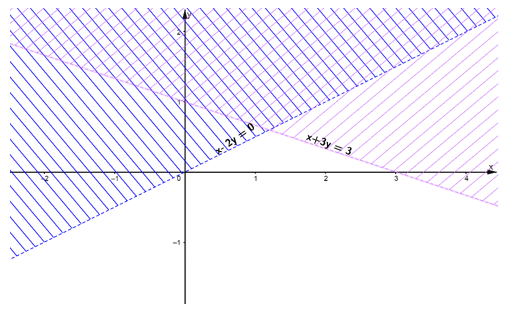
Vậy miền nghiệm của hệ bất phương trình trên là miền không bị gạch chéo.

Bài 3 trang 39 Toán lớp 10 Tập 1: Một công ty dự định sản xuất hai loại sản phẩm A và B. Các sản phẩm này được chế tạo từ ba loại nguyên liệu I, II, III. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại cần dùng để sản xuất 1 kg sản phẩm được cho trong bảng sau:

Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất ? Biết rằng, mỗi kilogam sản phẩm loại A lãi 30 triệu đồng, mỗi sản phẩm loại B lãi 50 triệu đồng.

Lời giải:

Gọi x và y lần lượt là số kilôgam của sản phẩm loại A và loại B.

Theo đề ta có:

+ Số kilôgam nguyên liệu I dùng để sản xuất ra 2 loại sản phẩm không vượt quá 8kg nên 2x + y ≤ 8

+ Số kilôgam nguyên liệu II dùng để sản xuất ra 2 loại sản phẩm không vượt quá 24kg nên 4x + 4y ≤ 24 hay x + y ≤ 6

+ Số kilôgam nguyên liệu III dùng để sản xuất ra 2 loại sản phẩm không vượt quá 24kg nên x + 2y ≤ 8

Suy ra hệ bất phương trình mô tả các điều kiện ràng buộc là: $\left\{\begin{array}{l}2x+y\le 8\\ x+y\le 6\\ x+2y\le 8\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình : 2x + y ≤ 8

Vẽ đường thẳng 2x + y – 8 = 0 đi qua hai điểm (4 0) và (0; 8).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng 2x + y – 8 = 0 và 0.2 + 0 – 8 = -8 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình : x + y ≤ 6

Vẽ đường thẳng x + y - 6 = 0 đi qua hai điểm (6; 0); (0; 6).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng x + y – 6 = 0 và 0 + 0 – 6 = - 6 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía bên phải trục tung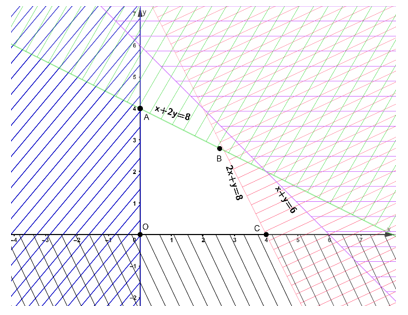

Miền nghiệm của hệ bất phương trình  là tứ giác OABC với các đỉnh O(0; 0);  A(0; 4);  B;$(\frac{8}{3};\frac{8}{3})$ C(4; 0).

Gọi F là số tiền lãi thu được (đơn vị: triệu đồng), ta được: F = 30x + 50y.

Giá trị của F tại các đỉnh của tứ giác:

Tại O(0; 0) ta có: F = 30.0 + 50.0 = 0;

Tại A(0; 4) ta có: F = 30.0 + 50.4 = 200;

Tại B$(\frac{8}{3};\frac{8}{3})$ ta có: ;$F=30.\frac{8}{3}+50.\frac{8}{3}=\frac{640}{3}$

Tại C(4; 0) ta có: F = 30.4 + 50.0 = 120;

F đạt giá trị lớn nhất bằng $\frac{640}{3}$ tại B.$(\frac{8}{3};\frac{8}{3})$

Vậy công ty cần sản xuất 8/3 kilôgam sản phẩm loại A và 8/3 kilôgam sản phẩm loại

B để số tiền lãi thu về là lớn nhất.

Bài 4 trang 39 Toán lớp 10 Tập 1: Một công ty cần mua các tủ đựng hồ sơ. Có hai loại tủ: Tủ loại A chiếm 3 m² sàn, loại này có sức chứa 12 m³ và có giá 7,5 triệu đồng ; tủ loại B chiếm 6 m² sàn, loại này có sức chứa 18 m³ và có giá 5 triệu. Cho biết công ty chỉ thu xếp được nhiều nhất là 60 m² mặt bằng cho chỗ đựng hồ sơ và ngân sách mua tủ không quá 60 triệu đồng. Hãy lập kế hoạch mua sắm để công ty có thể được thể tích đựng hồ sơ lớn nhất.

Lời giải:

Gọi x và y lần lượt là kích thước của tủ hồ sơ loại A và loại B (x ≥ 0, y ≥ 0)

Theo đề ta có:

+ Công ty chỉ thu xếp được nhiều nhất là 60 m² mặt bằng cho chỗ đựng hồ sơ nên

3x + 6y ≤ 60 hay x + 2y ≤ 20.

+ Ngân sách được sử dụng để mua tủ không quá 60 triệu đồng nên 7,5x + 5y ≤ 60.

Suy ra hệ bất phương trình mô tả các điều kiện ràng buộc là: $\left\{\begin{array}{l}x+2y\le 20\\ 7,5x+5y\le 60\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình : x + 2y ≤ 20

Vẽ đường thẳng x + 2y - 20 = 0 đi qua hai điểm (20; 0) và (0; 10).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng x + 2y – 20 = 0 và 0 + 2.0 – 20 = - 20  < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình : 7,5x + 5y ≤ 60

Vẽ đường thẳng 7,5x + 5y – 60 = 0 đi qua hai điểm (8; 0) và (0; 12).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng 7,5x + 5y – 60 = 0 và 7,5.0 + 5.0 – 60 = -60 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía bên phải trục tung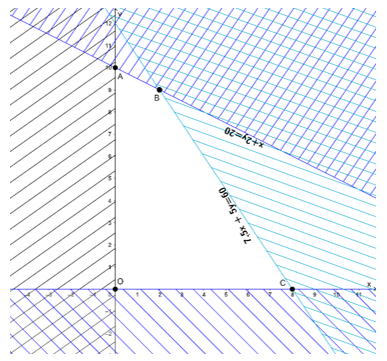

Miền nghiệm là tứ giác OABC với các đỉnh O(0; 0); A(0; 10); B(2; 9) ;C(8; 0).

Gọi F là thể tích để đựng hồ sơ (đơn vị: m³), ta được: F = 12x + 18y.   

Giá trị của F tại các đỉnh của tứ giác:

Tại O(0; 0) ta có: F = 12.0 + 18.0 = 0;

Tại A(0; 10) ta có: F = 12.0 + 18.10 = 180;

Tại B(2; 9) ta có: F = 12.2 + 18.9 = 186;

Tại C(8; 0) ta có: F = 12.8 + 18.0 = 96;

F đạt giá trị lớn nhất bằng 186 tại B(2; 9).

Vậy công ty cần phải mua 2 tủ loại A và 9 tủ loại B để có thể tích đựng hồ sơ lớn nhất.

Bài 5 trang 39 Toán lớp 10 Tập 1: Một nông trại thu hoạch được 180 kg cà chua và 15 kg hành tây. Chủ nông trại muốn làm các hũ tương cà để bán. Biết rằng, để làm ra một hũ tương cà loại A cần 10 kg cà chua cùng với 1kg hành tây và khi bán lãi được 200 nghìn đồng, còn để làm được một hũ tương cà loại B cần 5 kg cà chua cùng với 0,25 kg hành tây và khi bán lãi được 150 nghìn đồng. Thăm dò thị hiếu của khách hàng cho thấy cần phải làm số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B. Hãy giúp chủ nông trại lập kế hoạch làm tương cà để có được nhiều tiền lãi nhất.

Lời giải:

Gọi x và y lần lượt là số lượng hũ tương cà loại A và loại B.

+ Số kg cà chua để làm 2 loại tương ớt không được vượt quá 180 kg nên 10x + 5y ≤180  hay 2x + y ≤ 36

+ Số kg hành tây để làm 2 loại tương ớt không được vượt quá 15 kg nên x + 0,25y ≤ 15

+ Theo yêu cầu cần phải làm số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B nên x ≥ 3,5y

Suy ra hệ bất phương trình mô tả các điều kiện ràng buộc là:$\left\{\begin{array}{l}2x+y\le 36\\ x+0,25y\le 15\\ x\ge 3,5y\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình : 2x + y ≤ 36

Vẽ đường thẳng 2x + y - 36 = 0 đi qua hai điểm (18; 0) và (0; 36).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng 2x + y – 36 = 0 và 2.0 + 0 – 36 = - 36  < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình : x + 0,25y ≤ 15

Vẽ đường thẳng x + 0,25y – 15 = 0 đi qua hai điểm (15; 0); (0; 60).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng x + 0,25y – 15 = 0 và 0

+ 0,25.0 - 15 = -15< 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình : x ≥  3,5y hay x - 3,5y ≥ 0

Vẽ đường thẳng x - 3,5y = 0 đi qua hai điểm (0; 0); (7; 2).

Xét gốc toạ độ A(1; 1) ta thấy: A không thuộc đường thẳng x - 3,5y = 0 và 1 - 3,5.1 = -2.5 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm A

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía bên phải trục tung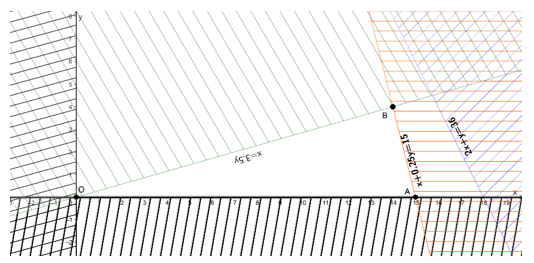

Miền nghiệm là tam giác OAB với các đỉnh O(0; 0); A(15; 0); B(14; 4).

Gọi F là số tiền lãi thu được (đơn vị: nghìn đồng), ta được: F = 200x + 150y.                                                                                                     

Giá trị của F tại các đỉnh của tam giác:

Tại O(0; 0) ta có: F = 200.0 + 150.0 = 0;

Tại A(15; 0) ta có: F = 200.15 + 150.0 = 3 000;

Tại B(14; 4) ta có: F = 200.14 + 150.4 = 3 400;

F đạt giá trị lớn nhất bằng 3 400 tại B(14; 4).

Vậy chủ nông trại cần làm 14 hũ tương cà loại A và 4 hũ tương cà loại B để thu được số tiền lãi lớn nhất.

Bài 6 trang 39 Toán lớp 10 Tập 1: Một xưởng sản xuất có hai máy đặc chủng A, B sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng máy A trong 6 giờ và dùng máy B trong 2 giờ. Để sản xuất một tấn sản phẩm Y cần dùng máy A trong 2 giờ và dùng máy B trong 2 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm. Máy A làm việc không quá 12 giờ một ngày; máy B làm việc không quá 8 giờ một ngày. Một tấn sản phẩm X lãi 10 triệu đồng và một tấn sản phẩm Y lãi 8 triệu đồng. Hãy lập kế hoạch sản xuất mỗi ngày sao cho tổng số tiền lãi cao nhất.

Lời giải:

Gọi x và y lần lượt là số tấn loại sản phẩm X và Y của nhà máy.

Theo đề ta có:

+ Thời gian làm việc của máy A để sản xuất ra hai loại sản phẩm X, Y không vượt qua 12 giờ nên 6x + 2y ≤ 12 hay 3x + y ≤ 6

+ Thời gian làm việc của máy B để sản xuất ra hai loại sản phẩm X, Y không vượt qua 8 giờ nên 2x + 2y ≤ 8 hay x + y ≤ 4

Suy ra hệ bất phương trình mô tả các điều kiện ràng buộc là: $\left\{\begin{array}{l}3x+y\le 6\\ x+y\le 4\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình : 3x + y ≤ 6

Vẽ đường thẳng 3x + y - 6 = 0 đi qua hai điểm (2; 0); (0; 6).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng 3x + y - 6 = 0  và 3.0 + 0 - 6 = - 6  < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình : x + y ≤ 4

Vẽ đường thẳng x + y – 4 = 0 đi qua hai điểm (4; 0); (0; 4).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng x + y – 4 = 0 và 0 + 0 - 4 = - 4< 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía bên phải trục tung

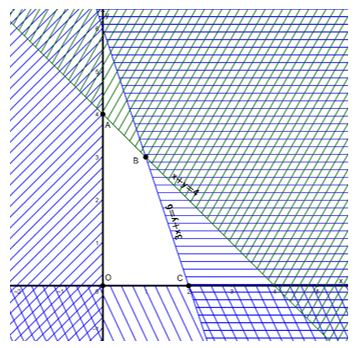
Miền nghiệm của hệ bất phương trình là tứ giác OABC với các đỉnh O(0; 0); A(0; 4); B(1; 3); C(2; 0).

Gọi F là số tiền lãi thu được (đơn vị: triệu đồng), ta được: F = 10x + 8y.                                                                                                              

Giá trị của F tại các đỉnh của tứ giác:

Tại O(0; 0) ta có: F = 10.0 + 8.0 = 0;

Tại A(0; 4) ta có: F = 10.0 + 8.4 = 32;

Tại B(1; 3) ta có: F = 10.1 + 8.3 = 34;

Tại C(2; 0) ta có: F = 10.2 + 8.0 = 20;

F đạt giá trị lớn nhất bằng 34 tại B(1; 3).

Vậy mỗi ngày cần sản xuất 1 tấn sản phẩm loại X và 3 tấn sản phẩm loại Y để thu được số tiền lãi lớn nhất.

Giải Toán 10 Bài 1: Mệnh đề - Chân trời sáng tạo

Giải Toán 10 Bài 2: Tập hợp - Chân trời sáng tạo

Giải Toán 10 Bài 3: Các phép toán trên tập hợp - Chân trời sáng tạo

Giải Toán 10 Bài tập cuối chương 1 - Chân trời sáng tạo