Giải bài tập Toán 10 Bài 1: Tọa độ của vectơ 

Hoạt động khởi động trang 38 Toán lớp 10 Tập 2: Hãy tìm cách xác định vị trí các quân mã trên bàn cờ vua.

Lời giải:

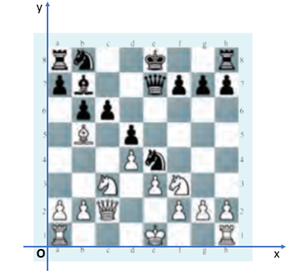
Để xác định vị trí quân mã trên bàn cờ vua ta gắn bàn cờ vua với hệ trục tọa độ Oxy như hình vẽ trên.

Khi đó, với mỗi vị trí của quân mã ta dõng thẳng xuống hai trục tọa độ Ox và Oy từ đó xác định được tọa độ tương ứng là (x; y).

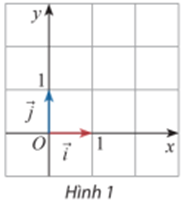
Hoạt động khám phá 1 trang 38 Toán lớp 10 Tập 2: Hãy nêu nhận xét về độ lớn, phương và chiều của  $\overrightarrow{i}$ trên trục Ox và  $\overrightarrow{j}$  trên trục Oy (Hình 1).

Lời giải:

Vì khoảng cách giữa điểm đầu và điểm cuối của hai vectơ $\overrightarrow{i}$  và $\overrightarrow{j}$  bằng 1 đơn vị nên vectơ đều có độ lớn bằng 1, tức là  $\left|\overrightarrow{i}\right|$ = 1 và $\left|\overrightarrow{j}\right|$  = 1.

Phương của vectơ $\overrightarrow{i}$  trùng với trục Ox, chiều của vectơ $\overrightarrow{i}$  trùng với chiều dương của trục Ox.

Phương của vectơ $\overrightarrow{j}$  trùng với trục Oy, chiều của vectơ $\overrightarrow{j}$  trùng với chiều dương của trục Oy.

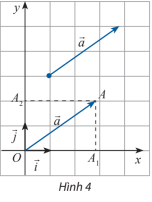
Hoạt động khám phá 2 trang 38 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho một vectơ $\overrightarrow{a}$ tùy ý. Vẽ  $\overrightarrow{OA}$ = $\overrightarrow{a}$  và gọi A₁, A₂ lần lượt là hình chiếu vuông góc của A lên Ox và Oy (Hình 4). Đặt $\overrightarrow{O{A}_1}$ = x $\overrightarrow{i}$ , $\overrightarrow{O{A}_2}$ = y $\overrightarrow{j}$ . Biểu diễn vectơ  $\overrightarrow{a}$ theo hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$ . 

Lời giải:

Theo quy tắc hình bình hành ta có: $\overrightarrow{OA}=\overrightarrow{O{A}_1}+\overrightarrow{O{A}_2}$ .

Mà $\overrightarrow{OA}$ = $\overrightarrow{a}$  và $\overrightarrow{O{A}_1}$ = x $\overrightarrow{i}$ , $\overrightarrow{O{A}_2}$ = y $\overrightarrow{j}$ nên ta có $\overrightarrow{OA}=\overrightarrow{O{A}_1}+\overrightarrow{O{A}_2}$ ⇔ $\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}$ .

Vậy$\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}$.

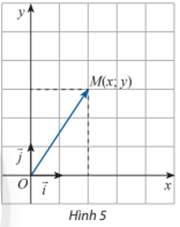
Hoạt động khám phá 3 trang 39 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ  $\overrightarrow{OM}$.

Lời giải:

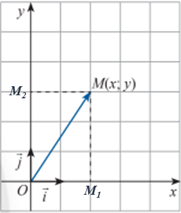
Gọi M1 và M2 lần lượt là hình chiếu vuông góc của M lên Ox và Oy.

Khi đó $\overrightarrow{OM}=\overrightarrow{O{M}_1}+\overrightarrow{O{M}_2}$  (quy tắc hình bình hành)

Mặt khác, vì điểm M(x; y) nên OM1 = x và OM2 = y.

Suy ra $\overrightarrow{O{M}_1}=x\overrightarrow{i}$  và $\overrightarrow{O{M}_2}=y\overrightarrow{j}$ .

Do đó $$$\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}$ .

Vậy $\overrightarrow{OM}$  = (x; y).

Thực hành 1 trang 40 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho ba điểm D(−1; 4), E(0; −3), F(5; 0).

a) Vẽ các điểm D, E, F trên mặt phẳng Oxy.

b) Tìm tọa độ của các vectơ  $\overrightarrow{OD}$, $\overrightarrow{OE}$ , $\overrightarrow{OF}$ .

c) Vẽ và tìm tọa độ của hai vectơ đơn vị  $\overrightarrow{i}$ ,  $\overrightarrow{j}$ lần lượt trên hai trục tọa độ Ox, Oy.

Lời giải:

a) Ta vẽ được các điểm D, E, F trên mặt phẳng Oxy như sau :

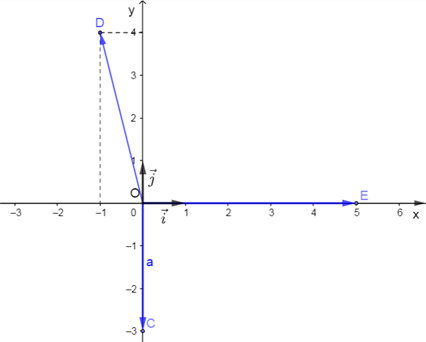
b) Vì D(−1; 4), E(0; −3), F(5; 0) nên $\overrightarrow{OD}$  = (−1; 4); $\overrightarrow{OE}$  = (0; −3); $\overrightarrow{OF}$  = (5; 0).

Vậy $\overrightarrow{OD}$  = (−1; 4); $\overrightarrow{OE}$  = (0; −3); $\overrightarrow{OF}$  = (5; 0).

c) Ta có $\overrightarrow{i}=1\overrightarrow{i}+0\overrightarrow{j}$  và $\overrightarrow{j}=0\overrightarrow{i}+1\overrightarrow{j}$  nên $\overrightarrow{i}$  = (1; 0) và $\overrightarrow{j}$  = (0; 1)

Vậy $\overrightarrow{i}$  = (1; 0) và $\overrightarrow{j}$  = (0; 1).

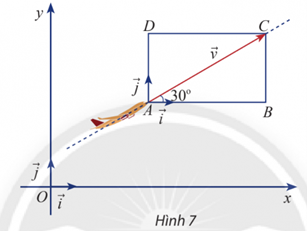
Vận dụng 1 trang 40 Toán lớp 10 Tập 2:  Một máy bay đang cất cánh với tốc độ 240 km/h theo phương hợp với phương nằm ngang một góc 30° (Hình 7).

a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD.

b) Biểu diễn vectơ vận tốc  $\overrightarrow{v}$  theo hai vectơ $\overrightarrow{i}$  và $\overrightarrow{j}$

c) Tìm tọa độ của $\overrightarrow{v}$.

Lời giải:

a) Vì ABCD là hình chữ nhật nên $\widehat{B}={90}^o$ , do đó tam giác ABC vuông tại B.

Ta có AB = AC.cos$\widehat{CAB}$  = AC. cos30° = $\left|\overrightarrow{v}\right|$ .cos30° = 240.$\frac{\sqrt{3}}{2}$ = $120\sqrt{3}$  (km).

Tương tự BC = AC.sin30° = 240.sin30°  = 120 (km).

Mặt khác, vì ABCD là hình chữ nhật nên DC = AB = $120\sqrt{3}$ (km) và AD = BC = 120 (km).

Vậy DC = AB = $120\sqrt{3}$  (km) và AD = BC = 120 (km).

b) Theo hình vẽ ta thấy hai vectơ $\overrightarrow{AB}$  và $\overrightarrow{i}$  cùng hướng và AB = $\left|\overrightarrow{AB}\right|$  = $120\sqrt{3}\left|\overrightarrow{i}\right|$  nên $\overrightarrow{AB}=120\sqrt{3}\overrightarrow{i}$ .

Tương tự, theo hình vẽ ta thấy hai vectơ $\overrightarrow{AD}$  và $\overrightarrow{j}$  cùng hướng và AD = $\left|\overrightarrow{AD}\right|$  = $120\left|\overrightarrow{j}\right|$ nên $\overrightarrow{AD}=120\overrightarrow{j}$ .

Mặt khác, ta có $\overrightarrow{v}$  = $\overrightarrow{AC}$  = $\overrightarrow{AB}+\overrightarrow{AD}$  (quy tắc hình bình hành)

⇒ $\overrightarrow{v}$ = $120\sqrt{3}\overrightarrow{i}+120\overrightarrow{j}$ .

Vậy  $\overrightarrow{v}$ = $120\sqrt{3}\overrightarrow{i}+120\overrightarrow{j}$ .

c) Từ $\overrightarrow{v}$  = $120\sqrt{3}\overrightarrow{i}+120\overrightarrow{j}$  (theo ý b).

Suy ra $\overrightarrow{v}$  = $\left(120\sqrt{3};120\right)$ .

Vậy $\overrightarrow{v}$  = $\left(120\sqrt{3};120\right)$ .

Hoạt động khám phá 4 trang 40 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho hai vectơ  $\overrightarrow{a}$ = (a₁; a₂), $\overrightarrow{b}$ = (b₁; b₂) và số thực k. Ta đã biết có thể biểu diễn từng vectơ $\overrightarrow{a}$ , $\overrightarrow{b}$ theo hai vectơ $\overrightarrow{i}$ , $\overrightarrow{j}$  như sau:  $\overrightarrow{a}$ = a₁ $\overrightarrow{i}$ + a₂ $\overrightarrow{j}$ ;  $\overrightarrow{b}$ = b₁ $\overrightarrow{i}$ + b₂ $\overrightarrow{j}$.

a) Biểu diễn từng vectơ: $\overrightarrow{a}$  + $\overrightarrow{b}$ ,  $\overrightarrow{a}$ − $\overrightarrow{b}$ , k$\overrightarrow{a}$  theo hai vectơ $\overrightarrow{i}$ , $\overrightarrow{j}$ .

b) Tìm: $\overrightarrow{a}$ . $\overrightarrow{b}$ theo tọa độ của hai vectơ  $\overrightarrow{a}$ và $\overrightarrow{b}$ .

Lời giải:

a) Ta có  

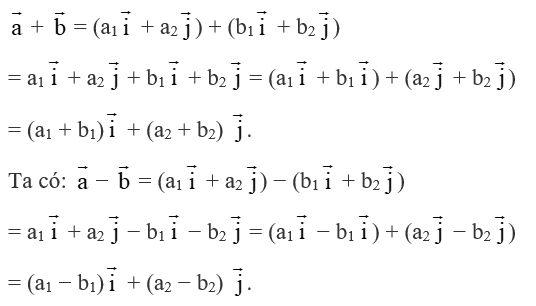
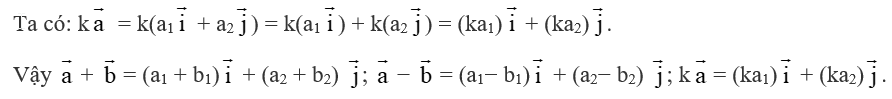
Thực hành 2 trang 41 Toán lớp 10 Tập 2:   Cho hai vectơ  $\overrightarrow{m}$ = (−6; 1),  $\overrightarrow{n}$ = (0; 2).

a) Tìm tọa độ các vectơ $\overrightarrow{m}$+ $\overrightarrow{n}$, $\overrightarrow{m}$− $\overrightarrow{n}$, 10$\overrightarrow{m}$, −4$\overrightarrow{n}$

b) Tính các tích vô hướng $\overrightarrow{m}$.$\overrightarrow{n}$ , (10$\overrightarrow{m}$ ). (−4$\overrightarrow{n}$ ).

Lời giải:

a) Ta có: $\overrightarrow{m}$  + $\overrightarrow{n}$ = (−6 + 0; 1 + 2) = (−6; 3)

$\overrightarrow{m}$ − $\overrightarrow{n}$ = (−6 − 0; 1 − 2) = (−6; −1)

10 $\overrightarrow{m}$  = (10. (−6); 10. 1) = (−60; 10)

−4$\overrightarrow{n}$ = (−4. 0; −4.2) = (0; −8)

Vậy $\overrightarrow{m}$  + $\overrightarrow{n}$  = (−6; 3); $\overrightarrow{m}$  − $\overrightarrow{n}$ = (−6; −1); 10 $\overrightarrow{m}$  = (−60; 10); −4$\overrightarrow{n}$  = (0; −8).

b) $\overrightarrow{m}$ . $\overrightarrow{n}$ = −6. 0 + 1. 2 = 2

(10$\overrightarrow{m}$ ).(−4$\overrightarrow{n}$) =  −60.0 + 10. (−8) =  −80.

Vậy $\overrightarrow{m}$.$\overrightarrow{n}$ = 2; (10$\overrightarrow{m}$ ).(−4$\overrightarrow{n}$ ) =  −80.

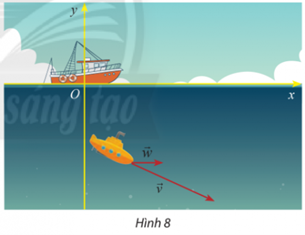
Vận dụng 2 trang 41 Toán lớp 10 Tập 2: Một thiết bị thăm dò đáy biển đang lặn với vận tốc $\overrightarrow{v}$  = (10; −8) (Hình 8). Cho biết vận tốc của dòng hải lưu vùng biển là $\overrightarrow{\text{w}}$ = (3,5; 0). Tìm tọa độ tổng hai vận tốc  $\overrightarrow{v}$ và  $\overrightarrow{\text{w}}$.

Lời giải:

Ta có: $\overrightarrow{v}$  + $\overrightarrow{\text{w}}$  = (10 +3,5; −8 + 0) = (13,5; −8).

Vậy tọa độ của vectơ tổng hai vận tốc $\overrightarrow{v}$ và  $\overrightarrow{\text{w}}$ là (13,5; −8).

Hoạt động khám phá 5 trang 41 Toán lớp 10 Tập 2: Cho hai điểm A(x_A; y_A), B(x_B; y_B). Từ biểu thức $\overrightarrow{AB}$ = $\overrightarrow{OB}$ − $\overrightarrow{OA}$ , tìm tọa độ vectơ  $\overrightarrow{AB}$ theo tọa độ hai điểm A, B.

Lời giải:

Vì A(xA; yA), B(xB; yB) nên $\overrightarrow{OA}$ = (xA; yA), $\overrightarrow{OB}$ = (xB; yB)

Ta có: $\overrightarrow{AB}$  = $\overrightarrow{OB}$  − $\overrightarrow{OA}$  = (xB − xA; yB − yA).

Vậy $\overrightarrow{AB}$  = $\overrightarrow{OB}$  −  $\overrightarrow{OA}$ = (xB − xA; yB − yA).

Thực hành 3 trang 42 Toán lớp 10 Tập 2: Cho E(9; 9); F(8; −7), G(0; −6). Tìm tọa độ của các vectơ $\overrightarrow{FE}$ , $\overrightarrow{FG}$ , $\overrightarrow{EG}$ .

Lời giải:

$\overrightarrow{FE}$= (9 − 8; 9 − (−7)) = (1; 16).

$\overrightarrow{FG}$ = (0 − 8; −6 −(−7)) = (−8; 1).

$\overrightarrow{EG}$ = (0 − 9; −6 − 9) = (−9; −15).

Vậy $\overrightarrow{FE}$ = (1; 16); $\overrightarrow{FG}$  = (−8; 1); $\overrightarrow{EG}$  = (−9; −15).

Hoạt động khám phá 6 trang 42 Toán lớp 10 Tập 2:  Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh là A(x_A; y_A), B(x_B; y_B), C(x_C; y_C). Gọi M(x_M; y_M) là trung điểm của đoạn thẳng AB, G(x_G; y_G) là trọng tâm của tam giác ABC.

a) Biểu thị vectơ $\overrightarrow{OM}$ theo hai vectơ  $\overrightarrow{OA}$ và $\overrightarrow{OB}$

b) Biểu thị vectơ $\overrightarrow{OG}$ theo ba vectơ  $\overrightarrow{OA}$, $\overrightarrow{OB}$ và  $\overrightarrow{OC}$.

c) Từ các kết quả trên, tìm tọa độ điểm M và G theo tọa độ của các điểm A, B, C.

Lời giải:

a) Vì M là trung điểm AB nên: $\overrightarrow{AM}$  = $\frac{1}{2}\overrightarrow{AB}$

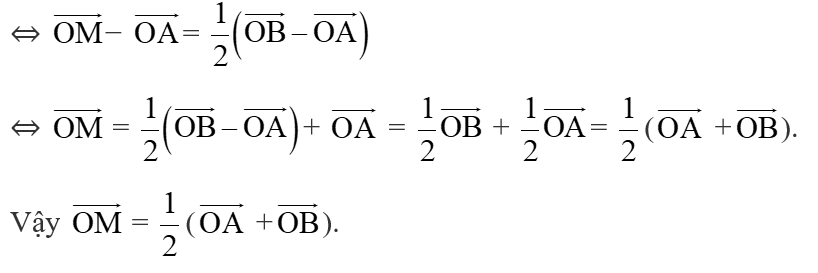
b) Vì G là trọng tâm tam giác ABC nên 3$\overrightarrow{OG}$ = $\overrightarrow{OA}$ + $\overrightarrow{OB}$ + $\overrightarrow{OC}$

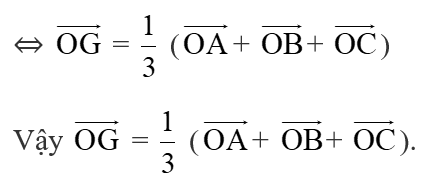
c) Vì A(x_A; y_A) nên $\overrightarrow{OA}$  = (x_A; y_A); B(x_B; y_B) nên $\overrightarrow{OB}$  = (x_B; y_B); C(x_C; y_C) nên $\overrightarrow{OC}$  = (x_C; y_C).

Khi đó: $\overrightarrow{OA}$  + $\overrightarrow{OB}$ = (x_A+ x_B; y_A+ y_B)

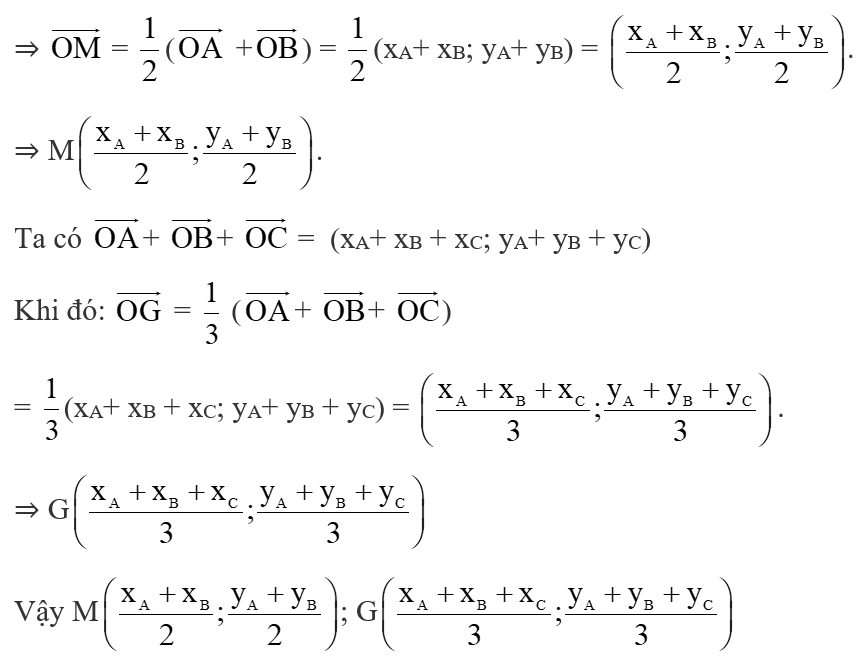
Thực hành 4 trang 43 Toán lớp 10 Tập 2:  Cho tam giác QRS có tọa độ các đỉnh là Q(7; − 2), R(−4; 9) và S(5; 8).

a) Tìm tọa độ trung điểm M của cạnh QS.

b) Tìm tọa độ trọng tâm G của tam giác QRS.

Lời giải:

a) Vì M là trung điểm của cạnh QS nên ta có : M$\left(\frac{x_Q+x_S}{2};\frac{y_Q+y_S}{2}\right)$

⇒ M $\left(\frac{7+5}{2};\frac{-2+8}{2}\right)$ ⇒ M$\left(2;3\right)$ .

Vậy M$\left(2;3\right)$ .

b) Vì G là trọng tâm của tam giác QRS nên ta có: G $\left(\frac{x_Q+x_R+x_S}{3};\frac{y_Q+y_R+y_S}{3}\right)$

⇒ G $\left(\frac{7+(-4)+5}{3};\frac{-2+9+8}{3}\right)$ ⇒ G $\left(\frac{8}{3};5\right)$.

Vậy G $\left(\frac{8}{3};5\right)$.

Hoạt động khám phá 7 trang 43 Toán lớp 10 Tập 2:  Cho hai vectơ $\overrightarrow{a}$ = (a₁; a₂), $\overrightarrow{b}$ = (b₁; b₂) và hai điểm A(x_A; y_A), B(x_B; y_B). Hoàn thành các phép biến đổi sau:

a) $\overrightarrow{a}$  ⊥  $\overrightarrow{b}$ ⇔ $\overrightarrow{a}$ . $\overrightarrow{b}$  = 0 ⇔ a1b1 + a2b2 = ..?..;

b) $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương ⇔ $\left\{\begin{array}{l}{a}_1=t{b}_1\\ a_2=t{b}_2\end{array}\right.$ hay $\left\{\begin{array}{l}{b}_1=k{a}_1\\ b_2=k{a}_2\end{array}\right.$ ⇔ a1b2 − a2b1 = ..?..;

c) $\left|\overrightarrow{a}\right|$  = $\sqrt{{\left(\overrightarrow{a}\right)}^2}$ = $\sqrt{\mathrm{..}?.}$ ;

d) $\overrightarrow{AB}$ = (xB – xA; yB – yA) ⇒ AB = $\sqrt{{\left(\overrightarrow{AB}\right)}^2}$ = $\sqrt{\mathrm{..}?.}$ ;

e) cos( $\overrightarrow{a}$,$\overrightarrow{b}$) = $\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}$ = $\frac{.?.}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$  ( $\overrightarrow{a}$, $\overrightarrow{b}$  khác $\overrightarrow{0}$ ).

Lời giải:

a) Vì$\overrightarrow{a}$⊥$\overrightarrow{b}$nên ta có ($\overrightarrow{a}$,$\overrightarrow{b}$) = 90°

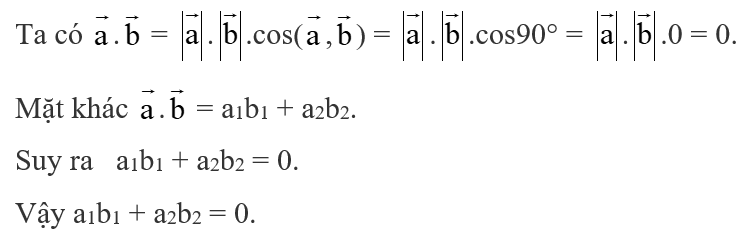
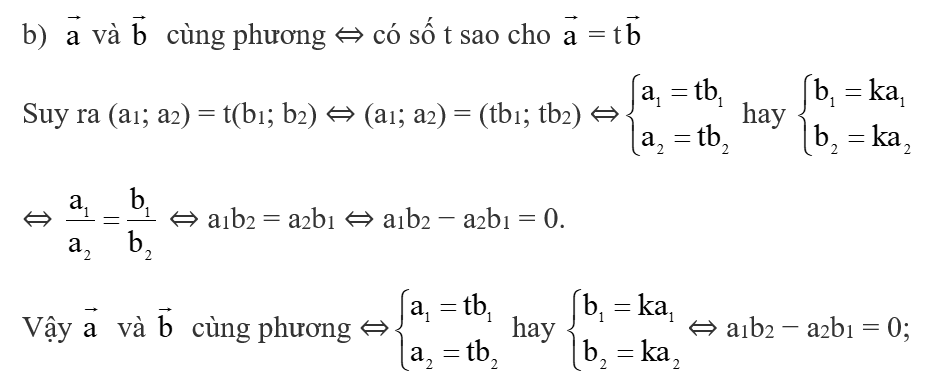
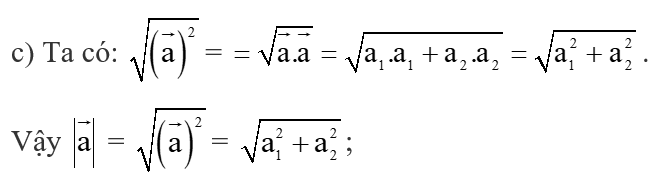
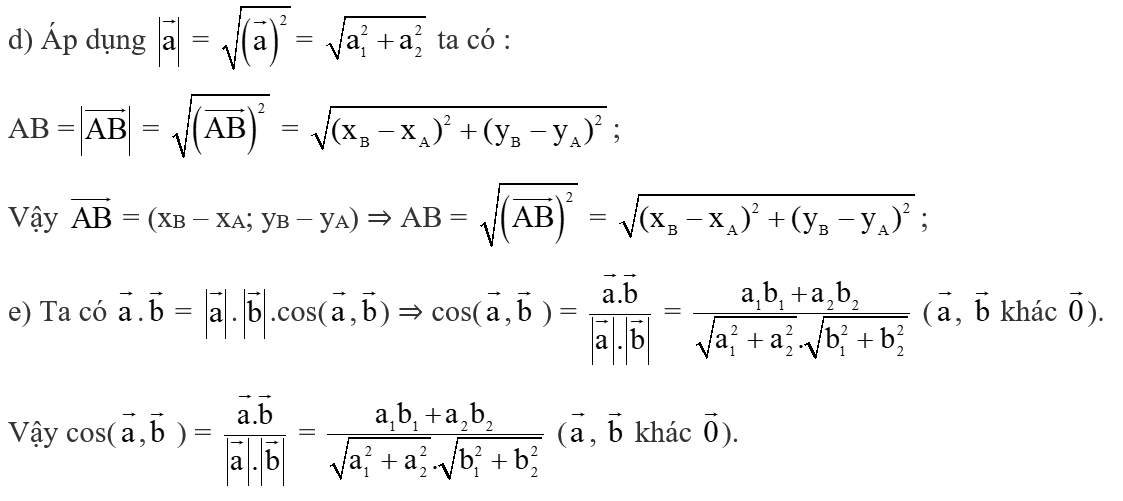
Thực hành 5 trang 44 Toán lớp 10 Tập 2:   Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ các đỉnh là D(2; 2), E(6;2) và F(2;6).

a) Tìm tọa độ điểm H là chân đường cao của tam giác DEF kẻ từ D.

b) Giải tam giác DEF.

Lời giải:

a) Gọi điểm H(x; y) là chân đường cao kẻ từ D của tam giác DEF.

Khi đó $\overrightarrow{DH}$ = (x − 2; y − 2), $\overrightarrow{EH}$ = (x − 6; y − 2), $\overrightarrow{EF}$ = (−4; 4).

H(x; y) là chân đường cao của tam giác DEF kẻ từ D, nên ta có:

$\overrightarrow{DH}$. $\overrightarrow{EF}$ = 0 ⇔ (x − 2).(−4) + (y − 2). 4 = 0 ⇔ −4x + 4y = 0 (1)

Hai vectơ $\overrightarrow{EH}$ , $\overrightarrow{EF}$  cùng phương ⇔ (x − 6). 4 − (y − 2). (−4) = 0 ⇔ 4x + 4y − 32 = 0 (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{array}{l}-4x+4y=0\\ 4x+4y-32=0\end{array}\right.$

Giải hệ trên ta được $\left\{\begin{array}{l}x=\text{ 4}\\ y=4\end{array}\right.$

Vậy H(4; 4)

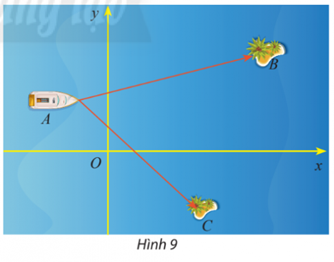
Vận dụng 3 trang 44 Toán lớp 10 Tập 2:  Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ B(50; 30) và C(32; −23). Một con tàu đang neo đậu tại điểm A(−10; 20).

a) Tính số đo của  $\widehat{BAC}$.

b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1 km. Tính khoảng cách từ con tàu đến mỗi hòn đảo.

Lời giải:

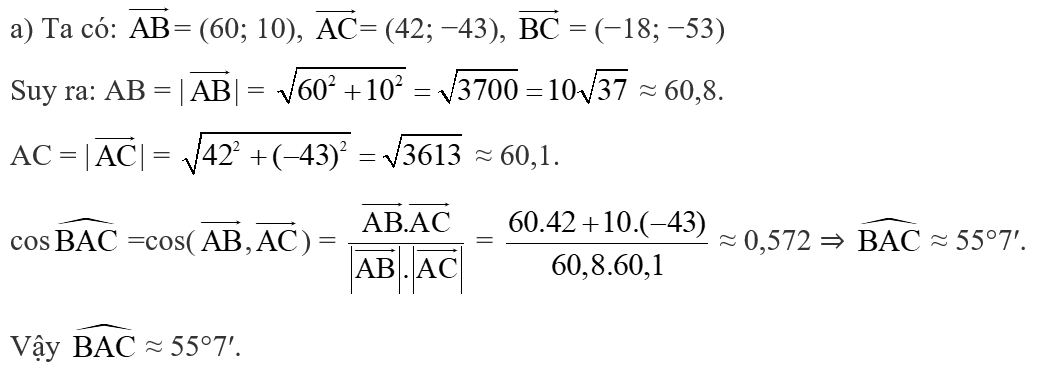
b) Mỗi đơn vị trên hệ trục tọa độ tương ứng với 1 km nên ta có:

Khoảng cách từ con tàu đến hòn đảo B là: AB ≈ 60,8 (km).

Khoảng cách từ con tàu đến hòn đảo C là AC ≈ 60,1 (km).

Vậy khoảng cách từ con tàu đến hòn đảo B khoảng 60,8 (km); Khoảng cách từ con tàu đến hòn đảo C khoảng 60,1 (km).

Bài tập 1 trang 44 Toán lớp 10 Tập 2:  Trên trục (O; $\overrightarrow{e}$) cho các điểm A, B, C, D có tọa độ lần lượt là 4; −1; −5; 0.

a) Vẽ trục và biểu diễn các điểm đã cho lên trên trục đó.

b) Hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng hướng hay ngược hướng?

Lời giải:

a) Ta có hình vẽ biểu diễn các điểm A, B, C, D như sau :

b) Quan sát hình vẽ ta thấy hai vectơ  $\overrightarrow{AB}$ và $\overrightarrow{CD}$  ngược hướng nhau.

Bài tập 2 trang 45 Toán lớp 10 Tập 2:  Chứng minh rằng:

a) $\overrightarrow{a}$  = (4; −6) và $\overrightarrow{b}$  = (−2; 3) là hai vectơ ngược hướng.

b) $\overrightarrow{a}$ = (−2; 3) và $\overrightarrow{b}$  = (−8; 12) là hai vectơ cùng hướng.

c)  $\overrightarrow{a}$ = (0; 4) và  $\overrightarrow{b}$ = (0; −4) là hai vectơ đối nhau.

Lời giải:

a) Ta có: (4; −6) = −2.(−2; 3) ⇒ $\overrightarrow{a}$   = −2 $\overrightarrow{b}$ ⇒  $\overrightarrow{a}$ và  $\overrightarrow{b}$ ngược hướng.

Vậy $\overrightarrow{a}$  = (4; −6) và  $\overrightarrow{b}$ = (−2; 3) là hai vectơ ngược hướng.

b) Ta có: (−8; 12) = 4(−2; 3) ⇒ $\overrightarrow{b}$ = 4$\overrightarrow{a}$

⇒ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng.

Vậy $\overrightarrow{a}$ = (−2; 3) và  $\overrightarrow{b}$ = (−8; 12) là hai vectơ cùng hướng.

c) Ta có: (0; 4) = −1.(0; −4) ⇒ $\overrightarrow{a}$   = −$\overrightarrow{b}$

Mặt khác |$\overrightarrow{a}$ | = $\sqrt{0^2+4^2}$ = 4; | $\overrightarrow{b}$ | =  $\sqrt{0^2+{(-4)}^2}$ = 4.

Suy ra $\overrightarrow{a}$   = −$\overrightarrow{b}$  và |$\overrightarrow{a}$ | = | $\overrightarrow{b}$ | = 4. Do đó 2 vectơ đối nhau.

Vậy$\overrightarrow{a}$= (0; 4) và $\overrightarrow{b}$ = (0; −4) là hai vectơ đối nhau.

Bài tập 3 trang 45 Toán lớp 10 Tập 2:  Tìm tọa độ các vectơ sau:

a) $\overrightarrow{a}$ = 2$\overrightarrow{i}$ +7$\overrightarrow{j}$ ;

b) $\overrightarrow{b}$ = − $\overrightarrow{i}$ + 3$\overrightarrow{j}$ ;

c) $\overrightarrow{c}$ = 4$\overrightarrow{i}$ ;

d) $\overrightarrow{d}$ = −9$\overrightarrow{j}$ .

Lời giải:

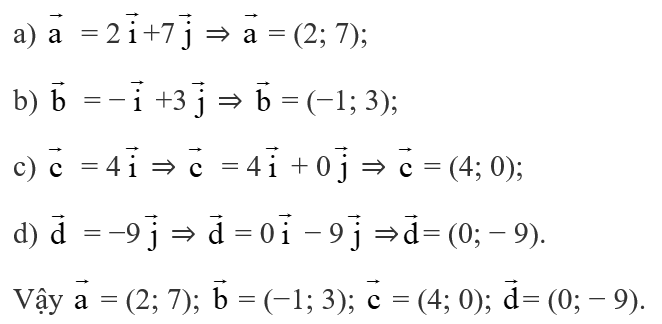
Bài tập 4 trang 45 Toán lớp 10 Tập 2:  Cho bốn điểm A(3; 5), B(4; 0), C(0; −3), D(2; 2). Trong các điểm đã cho, hãy tìm điểm:

a) Thuộc trục hoành;

b) Thuộc trục tung;

c) Thuộc đường phân giác của góc phần tư thứ nhất

Lời giải:

a) Điểm B(4; 0) có tung độ bằng 0 nên điểm B thuộc trục hoành.

b) Điểm C(0; −3) có hoành độ bằng 0 nên điểm C thuộc trục hoành.

c) Điểm D(2; 2) có hoành độ bằng tung độ nên điểm D thuộc đường phân giác của góc phần tư thứ nhất.

Vậy điểm B thuộc trục hoành, điểm C thuộc trục tung, điểm D thuộc đường phân giác của góc phần tư thứ nhất.

Bài tập 5 trang 45 Toán lớp 10 Tập 2:  Cho điểm M(x₀; y₀). Tìm tọa độ:

a) Điểm H là hình chiếu vuông góc của điểm M trên trục Ox;

b) Điểm M’ đối xứng với M qua trục Ox;

c) Điểm K là hình chiếu vuông góc của điểm M trên trục Oy;

d) Điểm M'' đối xứng với M qua trục Oy.

e) Điểm C đối xứng với điểm M qua gốc tọa độ.

Lời giải:

a)

a)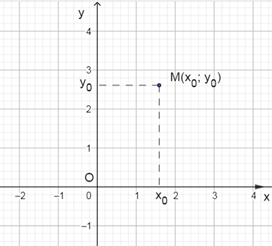

Do H là hình chiếu vuông góc của điểm M trên trục Ox nên điểm H có hoành độ bằng hoành độ của điểm M, và tung độ bằng 0.

⇒ H(x0; 0).

Vậy điểm H là hình chiếu vuông góc của điểm M trên trục Ox thì H(x0; 0).

b) M' đối xứng với M qua trục Ox ⇒ H là trung điểm của MM'

 $\left\{\begin{array}{l}{x}_H=\frac{x_M+x_{M\text{'}}}{2}\\ y_H=\frac{y_M+y_{M\text{'}}}{2}\end{array}\right.$⇔ $\left\{\begin{array}{l}{x}_0=\frac{x_0+x_{M\text{'}}}{2}\\ 0=\frac{y_0+y_{M\text{'}}}{2}\end{array}\right.$  ⇔ $\left\{\begin{array}{l}2x_0=x_0+x_{M\text{'}}\\ 0=y_0+y_{M\text{'}}\end{array}\right.$⇔ $\left\{\begin{array}{l}{x}_{M\text{'}}=x_0\\ y_{M\text{'}}=-y_0\end{array}\right.$

Vậy điểm M’ đối xứng với M qua trục Ox thì M’ có tọa độ là: M'(x0; −y0).

c) Do điểm K là hình chiếu vuông góc của điểm M trên trục Oy nên K có hoành độ bằng 0 và tung độ bằng tung độ của điểm M, tức là K(0; y0)

Vậy điểm K là hình chiếu vuông góc của điểm M trên trục Oy thì K có tọa độ là: K(0; y0).

d) M'' đối xứng với M qua trục Oy ⇒ K là trung điểm của MM''

 $\left\{\begin{array}{l}{x}_K=\frac{x_M+x_{M\text{'}\text{'}}}{2}\\ y_K=\frac{y_M+y_{M\text{'}\text{'}}}{2}\end{array}\right.$⇔ $\left\{\begin{array}{l}0=\frac{x_0+x_{M\text{'}\text{'}}}{2}\\ y_0=\frac{y_0+y_{M\text{'}\text{'}}}{2}\end{array}\right.$ ⇔ $\left\{\begin{array}{l}{x}_{M\text{'}\text{'}}=-x_0\\ y_{M\text{'}\text{'}}=y_0\end{array}\right.$

⇒ M''(−x0; y0).

Vậy điểm M'' đối xứng với M qua trục Oy thì M''(−x0; y0).

e) Vì C đối xứng với M qua gốc tọa độ O nên O là trung điểm của CM.

$\left\{\begin{array}{l}{x}_O=\frac{x_M+x_C}{2}\\ y_O=\frac{y_M+y_C}{2}\end{array}\right.$⇔$\left\{\begin{array}{l}0=\frac{x_0+x_C}{2}\\ 0=\frac{y_0+y_C}{2}\end{array}\right.$⇔ $\left\{\begin{array}{l}{x}_C=-x_0\\ y_C=-y_0\end{array}\right.$

⇒ C(−x0; −y0).

Vậy điểm C đối xứng với điểm M qua gốc tọa độ thì C có tọa độ là: C(−x0; −y0).

Bài tập 6  trang 45 Toán lớp 10 Tập 2:  Cho ba điểm A(2; 2); B(3; 5), C(5; 5).

a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

b) Tìm tọa độ giao điểm hai đường chéo của hình bình hành.

c) Giải tam giác ABC.

Lời giải:

a) Xét D(x; y). Ta có: $\overrightarrow{AB}$ = (1; 3); $\overrightarrow{DC}$ = (5 − x; 5 − y)

ABCD là hình bình hành ⇔ $\overrightarrow{AB}$ = $\overrightarrow{DC}$

⇔ $\left\{\begin{array}{l}1=5-x\\ 3=5-y\end{array}\right.$ ⇔ $\left\{\begin{array}{l}x=4\\ y=2\end{array}\right.$

Vậy D(4; 2).

b) Gọi M là giao điểm hai đường chéo của hình bình hành ABCD.

Khi đó M là trung điểm của BD

⇒ $\left\{\begin{array}{l}{x}_M=\frac{3+4}{2}=\frac{7}{2}\\ y_M=\frac{5+2}{2}=\frac{7}{2}\end{array}\right.$ ⇒ $M\left(\frac{7}{2};\frac{7}{2}\right)$

Vậy $M\left(\frac{7}{2};\frac{7}{2}\right)$ .

Bài tập 7 trang 45 Toán lớp 10 Tập 2: Cho tam giác ABC có các điểm M(2; 2), N(3; 4), P(5; 3) lần lượt là trung điểm của các cạnh AB, BC và CA.

a) Tìm tọa độ các đỉnh của tam giác ABC.

b) Chứng minh rằng trọng tâm của tam giác ABC và MNP trùng nhau.

c) Giải tam giác ABC.

Lời giải:

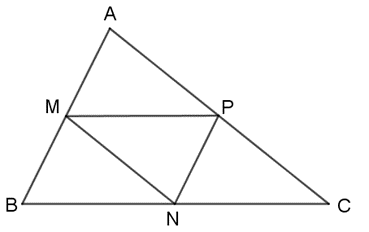
a) Ta có: $\overrightarrow{MP}$ = (3; 1); $\overrightarrow{BN}$ = (3 – xB; 4 – yB)

Có M là trung điểm cạnh AB, P là trung điểm cạnh AC nên MP là đường trung bình của tam giác ABC

⇒ MP // BC và MP = BN = $\frac{1}{2}$ BC ⇒ MPNB là hình bình hành.

Vậy A(4;1), B(0; 3), C(6; 5)

b) Gọi G là trọng tâm tam giác ABC, ta có: 

Vậy trọng tâm tam giác ABC trùng với trọng tâm tam giác MNP.

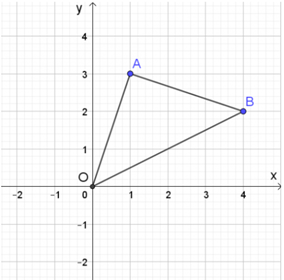
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB

b) Tính chu vi tam giác OAB.

c) Chứng minh rằng OA vuông góc với AB và từ đó tính diện tích tam giác OAB.

Lời giải: 

Bài tập 9 trang 45 Toán lớp 10 Tập 2:  Tính góc xen giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ trong các trường hợp sau:

a) $\overrightarrow{a}$ = (2; −3), $\overrightarrow{b}$ = (6; 4);

b) $\overrightarrow{a}$ = (3; 2); $\overrightarrow{b}$ = (5; −1);

c) $\overrightarrow{a}$ = (−2; $-2\sqrt{3}$ ), $\overrightarrow{b}$ = (3; $\sqrt{3}$ ).

Lời giải:

Bài tập 10 trang 45 Toán lớp 10 Tập 2:  Cho bốn điểm A(7; −3), B(8; 4), C(1; 5), D(0; −2). Chứng minh rằng tứ giác ABCD là hình vuông.

Lời giải:

Bài tập 11 trang 45 Toán lớp 10 Tập 2:  Một máy bay đang hạ cánh với vận tốc $\overrightarrow{v}$ = (−210; −42). Cho biết vận tốc của gió là $\overrightarrow{\text{w}}$ = (−12; −4) và một đơn vị trên hệ trục tọa độ tương ứng với 1 km. Tìm độ dài vectơ tổng hai vận tốc $\overrightarrow{v}$ và $\overrightarrow{\text{w}}$ .

Lời giải: