Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 5
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 10 Bài tập cuối chương 5 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài tập cuối chương 5. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài tập cuối chương 5
Bài tập
Bài 1 trang 102 Toán lớp 10 Tập 1: Cho ba vectơ đều khác vectơ . Các khẳng định sau đúng hay sai?
a) Nếu hai vectơ cùng phương với thì và cùng phương.
b) Nếu hai vectơ cùng ngược hướng với thì và cùng hướng.
Lời giải:
a) Hai vectơ và cùng phương nên (k1 ≠ 0).
Hai vectơ và cùng phương nên (k2 ≠ 0).
Khi đó .
Do đó hai vectơ và cùng phương.
Vậy khẳng định a đúng.
b) Hai vectơ và ngược hướng nên (k1 > 0).
Hai vectơ và ngược hướng nên (k2 > 0).
Khi đó với .
Do đó hai vectơ và cùng hướng.
Vậy khẳng định b đúng.
a) Tính độ dài của các vectơ .
b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng .
Lời giải:
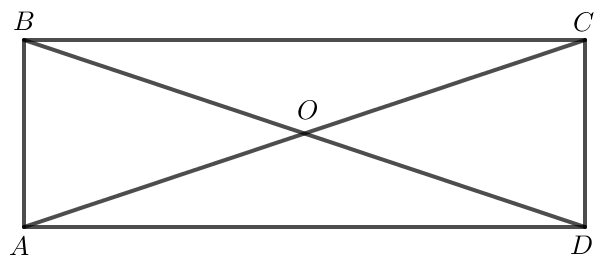
a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại B:
AC2 = AB2 + BC2
AC2 = a2 + (3a)2
AC2 = 10a2
AC = a (do AC là độ dài đoạn thẳng nên AC > 0)
Do ABCD là hình chữ nhật nên AC = BD = a.
Vậy .
b) Ta thấy = .
Do đó độ dài các vectơ đó bằng độ dài của AC và BD.
Vậy các cặp vectơ đối nhau và có độ dài bằng là: và ; và .
Lời giải:
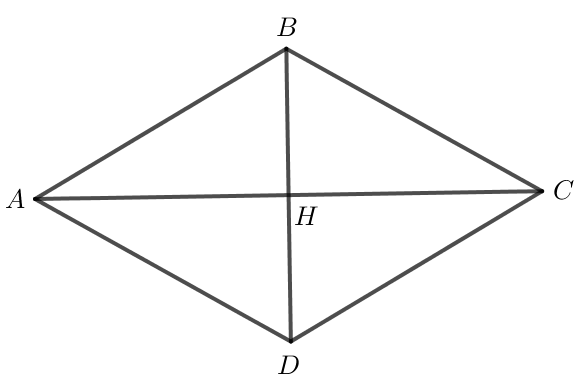
+) Tính :
Áp dụng quy tắc hình bình hành ta có .
Do đó .
Hình thoi ABCD có hai đường chéo AC và BD nên AC là tia phân giác của .
Do đó .
Tam giác ABC cân tại B nên .
Khi đó .
Áp dụng định lí côsin vào tam giác ABC ta có:
AC2 = AB2 + BC2 - 2.AB.BC.cos
AC2 = a2 + a2 - 2.a.a.cos 120o
AC2 = 2a2 + a2
AC2 = 3a2
AC = a (do AC là độ dài đoạn thẳng nên AC > 0)
Do đó .
+) Tính :
Ta có .
Do đó .
Tam giác ABD cân tại A có nên tam giác ABD đều.
Do đó BD = AB = a.
Do đó = a.
+) Tính :
Gọi H là giao điểm của AC và BD.
H là giao điểm hai đường chéo của hình thoi ABCD nên .
Do đó .
Khi đó .
Do đó .
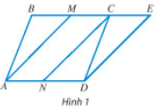
a) Tìm tổng của các vectơ và ; và ; và .
Lời giải:
M là trung điểm của BC nên BM = MC = BC.
N là trung điểm của AD nên AN = ND = AD.
Do ABCD là hình bình hành nên BC = AD.
Do đó BM = MC = AN = ND.
Do nên CE = AN.
Do đó BM = MC = AN = ND = CE.
Khi đó ta có AMCN, NCED là các hình bình hành.
a) +) Tính :
Ta có nên .
+) Tính :
Ta có nên .
+) Tính :
Ta có nên .
b) +) Tính :
Ta có .
+) Tính :
Ta có .
+) Tính :
Ta có nên .
c) Ta có và .
Do đó .
Lời giải:
a) thì .
Mà nên .
Do đó .
Vậy hai vectơ và cùng hướng.
b) thì .
Do là hai vectơ khác vectơ nên .
Do đó .
Vậy hai vectơ và vuông góc với nhau.
Bài 6 trang 103 Toán lớp 10 Tập 1: Cho . So sánh độ dài, phương và hướng của hai vectơ và .
Lời giải:
Do = 0 nên .
Trường hợp 1. Cả hai vectơ và đều là vectơ .
Khi đó hai vectơ và cùng hướng và có độ dài bằng nhau.
Trường hợp 2. Cả hai vectơ và đều khác vectơ .
Khi đó .
Do đó hai vectơ và cùng phương, ngược hướng và có độ dài bằng nhau.
Lời giải:
Phần thuận: thì trung điểm hai đoạn thẳng AD và BC trùng nhau.
Do nên hai vectơ , cùng hướng và AB = CD.
Do hai vectơ , cùng hướng nên ta có 2 trường hợp:
Trường hợp 1. Đường thẳng AB và CD trùng nhau, lại có AB = CD nên trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Trường hợp 2. Đường thẳng AB và CD song song với nhau.
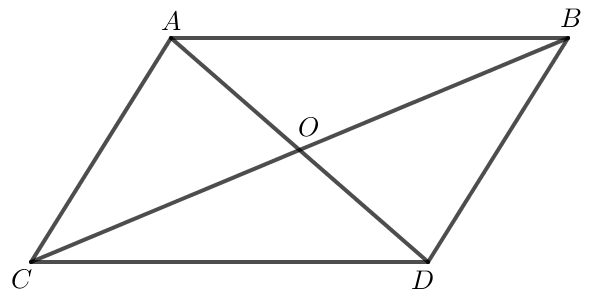
Đường thẳng AB và CD song song với nhau, lại có AB = CD nên ABDC là hình bình hành.
Khi đó tâm O của hình bình hành ABCD là giao điểm hai đường chéo AD và BC nên O là trung điểm của AD và BC tức trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Phần đảo: Trung điểm của hai đoạn thẳng AD và BC trùng nhau thì .
Trường hợp 1. Hai đường thẳng AD và BC trùng nhau.

Gọi trung điểm của AD và BC là O.
Do O là trung điểm của AD nên OA = OD.
Do O là trung điểm của BC nên OB = OC.
Do đó OB - OA = OC - OD hay AB = CD.
Ta thấy hai vectơ và cùng hướng và AB = CD nên .
Trường hợp 2. Hai đường thẳng AD và BC cắt nhau.
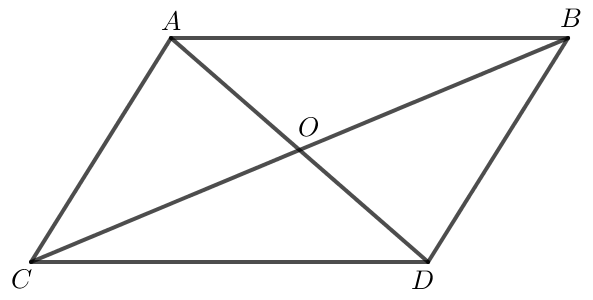
Hai đường thẳng AD và BC cắt nhau tại điểm O, điểm O là trung điểm của AD và BC nên ABDC là hình bình hành.
Do đó AB // CD và AB = CD.
Ta thấy hai vectơ và cùng hướng và AB = CD nên .
Lời giải:
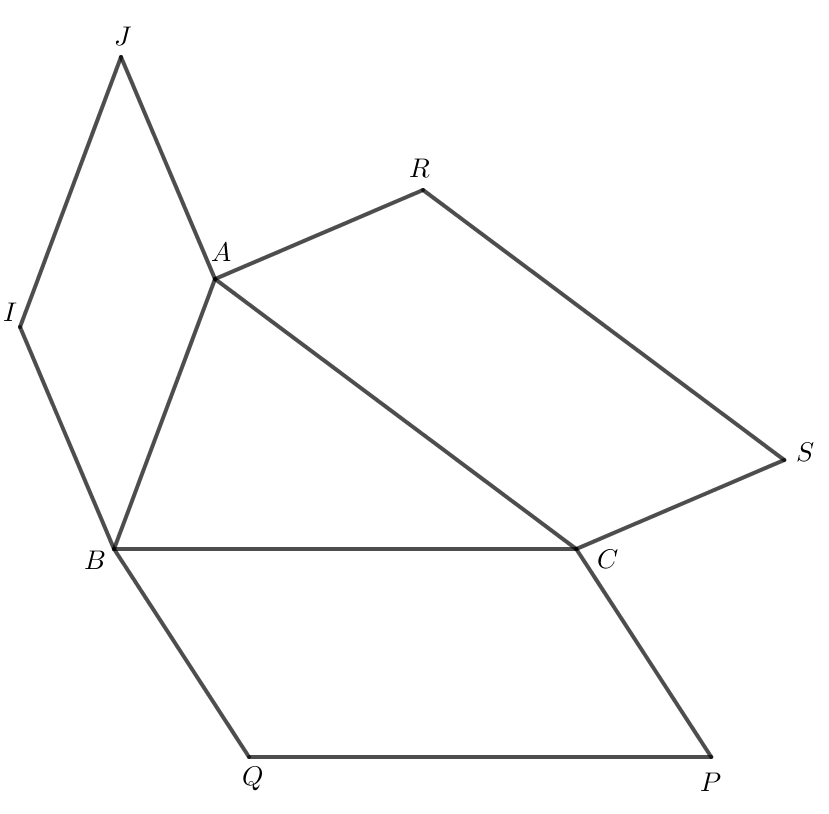
Ta có .
Do ABIJ là hình bình hành nên .
Do CARS là hình bình hành nên .
Do BCPQ là hình bình hành nên .
Do đó
.
Vậy .
Lời giải:
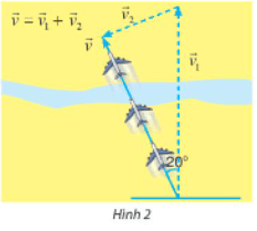
Trong hình trên ta có vectơ là tốc độ của máy bay bay về phía bắc, vectơ là tộc độ của máy bay so với mặt đất, vectơ là tốc độ của gió.
Khi đó độ dài ba vectơ và tạo thành độ dài ba cạnh của tam giác vuông.
Khi đó sin 20o = .
= 45 . sin 20o
≈ 15.
Vậy tốc độ của gió khoảng 15 m/s.
Lời giải:
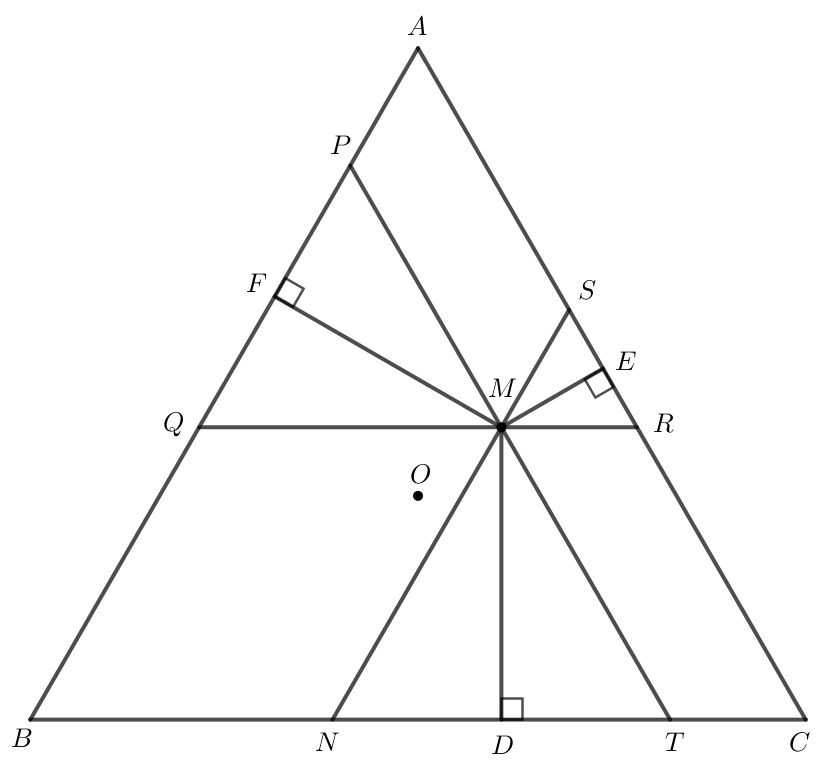
Tam giác ABC đều nên .
Qua M kẻ NS // AB, PT // AC, RQ // BC.
Do NS //AB nên và .
Do PT // AC nên và .
Do RQ // BC nên và .
Khi đó các tam giác MNT, MRS và MPQ là các tam giác đều.
Tam giác MNT đều có MD NT nên D là trung điểm của NT.
Tam giác MRS đều có ME RS nên E là trung điểm của RS.
Tam giác MPQ đều có MF PQ nên F là trung điểm của PQ.
Do D là trung điểm của NT nên .
Do E là trung điểm của RS nên .
Do F là trung điểm của PQ nên .
Do đó
Tứ giác MNBQ có MN // BQ và MQ // BN nên MNBQ là hình bình hành.
Tứ giác MTCR có MT // CR và MR // CT nên MTCR là hình bình hành.
Tứ giác MSAP có MP // AS và MS // AP nên MSAP là hình bình hành.
Khi đó áp dụng quy tắc hình bình hành ta có:
; ; .
Do đó .
Do O là trọng tâm của tam giác ABC nên hay
.
Do đó .
Lời giải:
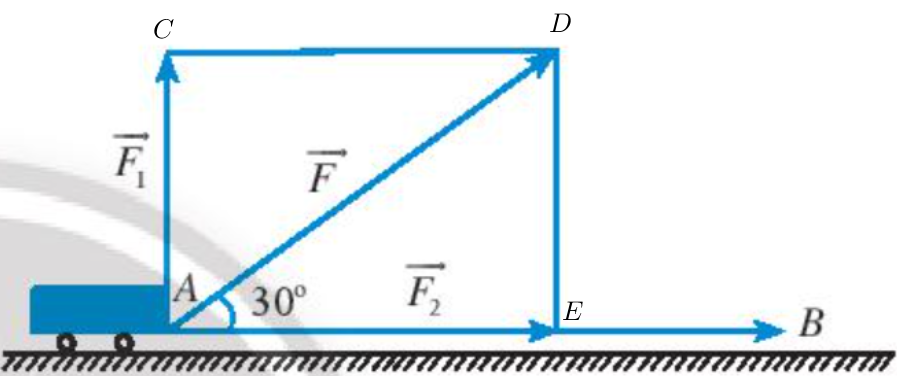
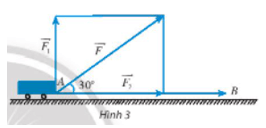
Đặt tên điểm đầu và điểm cuối của các vectơ như hình trên.
Tam giác ADE vuông tại E nên cos 30o =
AE = AD . cos 30o = 50 . = N.
Ta thấy nên J.
và là hai vectơ cùng hướng nên .
Khi đó = . 200 = J.
= 50 . 200 . = J.
Vậy công sinh bởi các lực và lần lượt là J, J, 0 J.
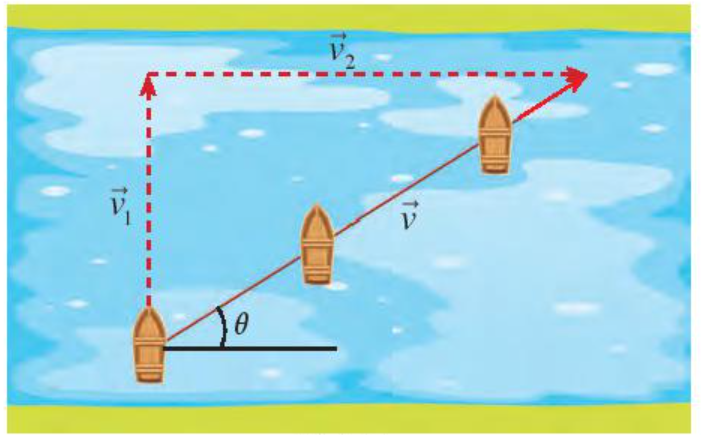
a) Tính độ dài của các vectơ .
b) Tốc độ dịch chuyển của thuyền so với bờ là bao nhiêu?
c) Hướng di chuyển của thuyền lệch một góc bao nhiêu so với bờ?
Lời giải:
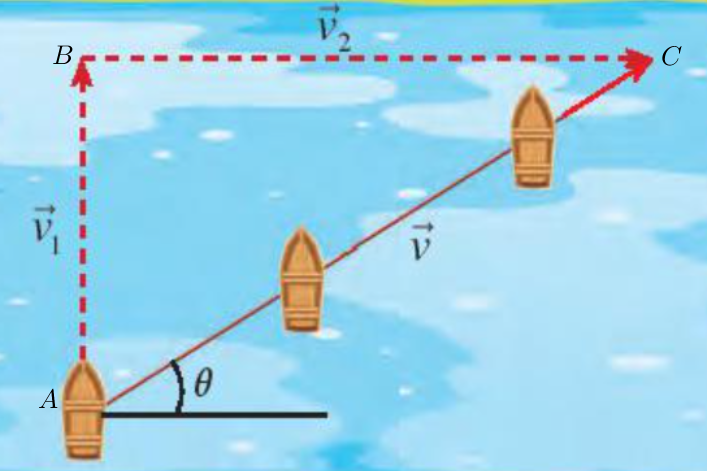
Đặt tên điểm đầu và điểm cuối của các vectơ như hình trên.
a) Ta có ; .
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:
AC2 = AB2 + BC2
AC = ≈ 1,4 (do AC là độ dài đoạn thẳng nên AC > 0)
≈ 1,4.
b) Khi đó tốc độ dịch chuyển của thuyền so với bờ khoảng 1,4 m/s.
c) Tam giác ABC vuông tại B nên .
≈ 32o
Ta có nên ≈ 32o.
Vậy hướng di chuyển của thuyền lệch một góc khoảng 32o so với bờ.