Giải bài tập Toán 10 Bài tập cuối chương 8 

Bài 1 trang 36 Toán lớp 10 Tập 2:

Một nhóm tình nguyện viên gồm 4 học sinh lớp 10A, 5 học sinh lớp 10B và 6 học sinh lớp 10C. Để tham gia một công việc tình nguyện, nhóm có bao nhiêu cách cử ra:

a) 1 thành viên của nhóm?

b) 3 thành viên của nhóm đang học ở ba lớp khác nhau?

c) 2 thành viên của nhóm đang học ở hai lớp khác nhau?

Lời giải:

a) Mỗi cách chọn 1 thành viên từ nhóm tình nguyên có 15 học sinh là một tổ hợp chập 1 của 15. Vậy có $C_{15}^1=15$  cách cử ra 1 thành viên của nhóm.

b) Có thể xem việc cử ra 3 thành viên của nhóm đang học ở ba lớp khác nhau là một công việc gồm 3 công đoạn:

Công đoạn 1: Cử ra 1 thành viên của lớp 10A có 4 cách chọn.

Công đoạn 2: Cử ra 1 thành viên của lớp 10B có 5 cách chọn.

Công đoạn 3: Cử ra 1 thành viên của lớp 10C có 6 cách chọn.

Áp dụng quy tắc nhân, có 4.5.6 = 120 cách cử ra 3 thành viên của nhóm đang học ở ba lớp khác nhau

c) Có thể xem việc cử ra 2 thành viên của nhóm đang học ở hai lớp khác nhau là một công việc gồm 3 phương án thực hiện:

Phương án 1 : Cử ra 1 thành viên lớp 10A và 1 thành viên lớp 10B, có 4.5 = 20 cách.

Phương án 2 : Cử ra 1 thành viên lớp 10A và 1 thành viên lớp 10C, có 4.6 = 24 cách.

Phương án 3 : Cử ra 1 thành viên lớp 10B và 1 thành viên lớp 10C, có 5.6 = 30 cách.

Áp dụng quy tắc cộng có 20 + 24 + 30 = 74 cách để cử ra 2 thành viên của nhóm đang học ở hai lớp khác nhau

Bài 2 trang 36 Toán lớp 10 Tập 2:

Một khoá số có 3 vòng số (mỗi vòng gồm 10 số từ 0 đến 9) như Hình 1. Người dùng cần đặt mật mã cho khoá là một dãy số có ba chữ số . Để mở khoá, cần xoay các vòng số để dãy số phía trước khoá trùng với mật mã đã chọn. Có bao nhiêu cách chọn mật mã cho khoá?

Lời giải:

Có thể coi việc tạo ra một dãy số mật mã có 3 chữ số là một công việc gồm 3 công đoạn. Mỗi công đoạn ứng với việc chọn 1 số trong 10 số cho mỗi vị trí của các vòng số.

Như vậy mỗi công đoạn có 10 cách chọn số

Theo quy tắc nhân, 3 công đoạn có 10.10.10 = 1000 cách chọn mật mã cho khoá.

Vậy có tất cả  1000 cách tạo mật mã.

Bài 3 trang 36 Toán lớp 10 Tập 2:

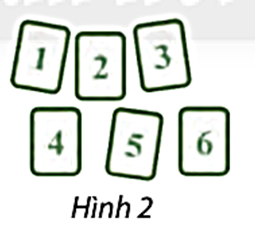
Từ 6 thẻ số như Hình 2, có thể ghép để tạo thành bao nhiêu:

a) Số tự nhiên có 6 chữ số?

b) Số tự nhiên lẻ có 6 chữ số?

c) Số tự nhiên có 5 chữ số?

d) Số tự nhiên có 5 chữ số lớn hơn 50 000?

Lời giải:

a) Mỗi số tự nhiên có sáu chữ số khác nhau được lập từ 6 chữ số lấy từ 6 tấm thẻ là 1; 2; 3; 4; 5; 6 là một hoán vị của sáu chữ số này. Do đó, số số tự nhiên lập được: P₆ = 6! = 6.5.4.3.2.1 = 720.

Vậy có 720 số tự nhiên lập thành từ các chữ số trên 6 tấm thẻ.

b) Việc tạo số tự nhiên lẻ có 6 chữ số là một công việc gồm 2 công đoạn:

Công đoạn 1: Chọn chữ số hàng đơn vị là chữ số lẻ, có 3 cách chọn (Chọn 1 hoặc 3 hoặc 5)

Công đoạn 2: Chọn 5 chữ số còn lại có: P₅ = 5! = 120 cách chọn

Vậy theo quy tắc nhân có: 3.120 = 360 số tự nhiên lẻ có 6 chữ số được tạo thành từ các chữ số đã cho.

c) Mỗi số tự nhiên có 5 chữ số được tạo thành từ việc ghép 5 thẻ số khác nhau. Do đó, mỗi số có 5 chữ số khác nhau được tạo thành từ 6 chữ số là một chỉnh hợp chập 5 của 6. Do đó, có thể lập được: $A_6^5=720$  (số).

Vậy có thể lập được 720 số thỏa mãn yêu cầu bài toán.

d) Việc sắp xếp các thẻ số tạo thành số tự nhiên có 5 chữ số lớn hơn 50000 là 1 công việc gồm 2 công đoạn:

Công đoạn 1: Chọn chữ số hàng chục nghìn, có 2 cách chọn (Chọn 5 hoặc 6)

Công đoạn 2: Ứng với chữ số hàng chục nghìn, chọn 4 chữ số từ 5 chữ số còn lại và sắp xếp các số vào các hàng tương ứng là một chỉnh hợp chập 4 của 5. Do đó có: $A_5^4=120$  cách chọn

Vậy có 120.2 = 240 cách ghép để tạo thành số tự nhiên có 5 chữ số lớn hơn 50000.

Bài 4 trang 36 Toán lớp 10 Tập 2:

Thực đơn tại một quán cơm văn phòng có 6 món mặn, 5 món rau và 3 món canh. Tại đây, một nhóm khách muốn chọn bữa trưa gồm cơm, 2 món mặn, 2 món rau và 1 món canh. Nhóm khách có bao nhiêu cách chọn?

Lời giải:

Có thể xem việc chọn các món án cho bữa trưa là một công việc gồm 3 công đoạn:

Công đoạn 1: chọn 2 món mặn, mỗi cách chọn 2 món mặn từ 6 món mặn là một tổ hợp chập 2 của 6 . Do đó, có $C_6^2=15$  cách chọn

Công đoạn 2: chọn 2 món rau, mỗi cách chọn 2 món rau từ 5 món rau là một tổ hợp chập 2 của 5 . Do đó, có $C_5^2=10$  cách chọn

Công đoạn 3: chọn 1 món canh, có 3 cách chọn

Áp dụng quy tắc nhân có 15.10.3 = 450 cách chọn thực đơn cho bữa trưa.

Vậy nhóm khách có 450 cách chọn thực đơn bữa trưa.

Bài 5 trang 36 Toán lớp 10 Tập 2:

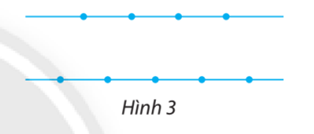
Cho 9 điểm nằm trên hai đường thẳng song song như Hình 3. Có bao nhiêu tam giác có các đỉnh là ba điểm trong các điểm đã cho ?

Lời giải:

Việc tạo thành hình tam giác từ 3 đỉnh là ba điểm trong 9 điểm nằm trên hai đường thẳng song song là một công việc có 2 phương án:

Phương án 1: Chọn 1 điểm thuộc đường thẳng trên và 2 điểm thuộc đường thẳng dưới có: 4. $C_5^2$  = 40 hình tam giác.

Phương án 2: Chọn 2 điểm thuộc đường thẳng trên và 1 điểm thuộc đường thẳng dưới có: 5. $C_4^2$ = 30 hình tam giác.

Vậy có thể tạo được 40 + 30 = 70 tam giác từ 9 điểm nằm trên 2 đường thẳng song song.

Bài 6 trang 36 Toán lớp 10 Tập 2:

Khai triển các biểu thức

a) ${\left(a-\frac{b}{2}\right)}^4$

b) (2x² + 1)⁵

Lời giải:

a) ${\left(a-\frac{b}{2}\right)}^4$ = $C_4^0{a}^4-C_4^1{a}^3.\frac{b}{2}+C_4^2{a}^2.{\left(\frac{b}{2}\right)}^2-C_4^{3}a.{\left(\frac{b}{2}\right)}^3+C_4^4{\left(\frac{b}{2}\right)}^4$

                  = a⁴ – 2a³b + $\frac{3}{2}$ a²b² – $\frac{1}{2}$ ab³ + $\frac{1}{16}$ b⁴.                         

b) (2x² + 1)⁵ = $C_5^0{\left(2x^2\right)}^5+C_5^1{\left(2x^2\right)}^4+C_5^2{\left(2x^2\right)}^3+C_5^3{\left(2x^2\right)}^2+C_5^4.2x^2+C_5^5$

                    = 32x¹⁰ + 80x⁸ + 80x⁶ + 40x⁴ + 10x² + 1.

Bài 7 trang 36 Toán lớp 10 Tập 2:

Hãy khai triển và rút gọn biểu thức :

(1 + x)⁴ + (1 – x)⁴

Sử dụng kết quả đó để tính gần đúng giá trị biểu thức 1,05⁴ + 0,95⁴

Lời giải:

Ta có: (1 + x)⁴ =  $C_4^0{x}^4+C_4^1{x}^3+C_4^2{x}^2+C_4^{3}x+C_4^4$ = x⁴ + 4x³ + 6x² + 4x + 1

(1 – x)⁴ = $C_4^0{x}^4-C_4^1{x}^3+C_4^2{x}^2-C_4^{3}x+C_4^4$ = x⁴ – 4x³ + 6x² – 4x + 1

Do đó: (1 + x)⁴ + (1 – x)⁴ = x⁴ + 4x³ + 6 x² + 4x + 1+ x⁴ – 4x³ + 6x² – 4x + 1

= 2x⁴ + 12x² + 2 (1).

Theo giả thiết ta có: 1 + x  = 1,05 và 1 – x = 0,95 suy ra x = 0,05

Thay x = 0,05 vào (1) ta có: 1,05⁴ + 0,95⁴ = 2.0,05⁴ + 12.0,05² + 2 ≈ 2,03.