Giải Toán 10 (Chân trời sáng tạo) Bài 4: Tích vô hướng của hai vectơ
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 10 Bài 4: Tích vô hướng của hai vectơ sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 4. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài 4: Tích vô hướng của hai vectơ
1. Góc giữa hai vectơ
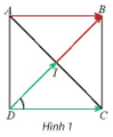
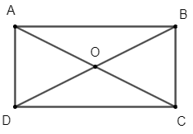
Khám phá 1 trang 98 Toán lớp 10 Tập 1: Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính .
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C.
c) Tìm hai vectơ cùng có điểm đầu là D và lần lượt bằng và .
Lời giải:
a) Hình vuông ABCD có tâm I nên IA = IB = IC = ID và AC BC tại I.
Do đó tam giác IDC vuông cân tại I.
Khi đó = 45o.
b) Vectơ có điểm đầu là D, điểm cuối là I là vectơ .
Vectơ có điểm đầu là D, điểm cuối là C là vectơ .
c) Vectơ có điểm đầu là D và bằng vectơ là vectơ .
Vectơ có điểm đầu là D và bằng vectơ là vectơ .
Lời giải:
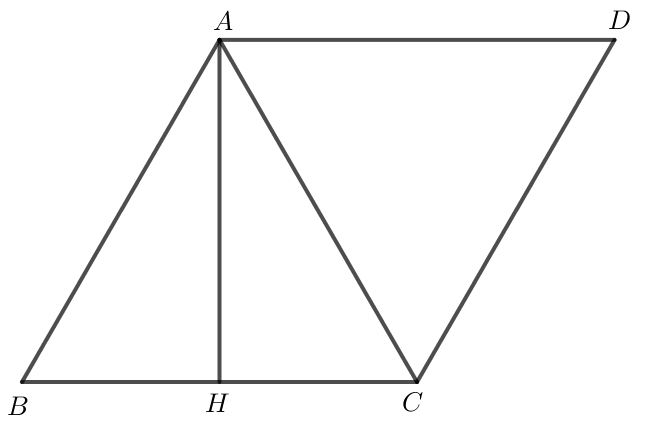
Dựng hình bình hành ABCD.
Do tam giác ABC đều nên = 60o, do đó = 60o.
Do ABCD là hình bình hành nên .
Do đó .
Do ABCD là hình bình hành nên .
Do đó = 180o - 60o = 120o.
Khi đó = 120o hay = 120o.
Tam giác ABC đều có H là trung điểm của BC nên AH vừa là đường trung tuyến, vừa là đường cao trong tam giác ABC.
Do đó AH BC nên = 90o.
Hai vectơ và cùng hướng nên = 0o.
Hai vectơ và ngược hướng nên = 180o.
2. Tích vô hướng của hai vectơ
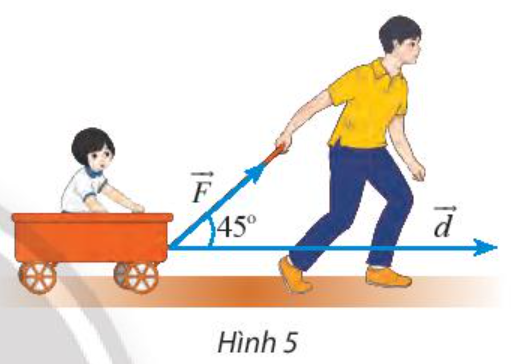
Lời giải:
Công sinh bởi lực bằng:
= 10 . 100 . cos 45o ≈ 707 J.
Vậy công sinh bởi lực khoảng 707 J.
Thực hành 2 trang 100 Toán lớp 10 Tập 1: Cho tam giác ABC vuông cân tại A, cạnh huyền bằng . Tính các tích vô hướng: .
Lời giải:
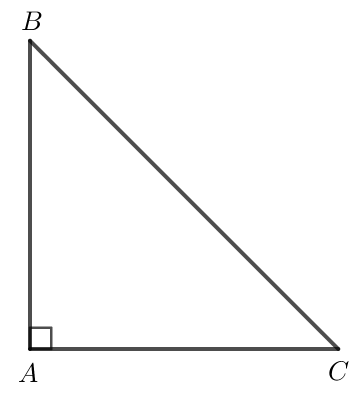
Do tam giác ABC vuông cân tại A nên AB AC.
Do đó .
Áp dụng định lí Pythagore vào tam giác ABC vuông cân tại A ta có:
AB2 + AC2 = BC2
2AB2 = 2
AB2 = 1
AB = 1 (do AB là độ dài đoạn thẳng nên AB > 0)
Tam giác vuông cân tại A nên = 45o.
Ta có .
= 1 . . cos = 1 . . cos 45o = 1.
Do đó = 1.
= 1 . . cos = 1 . . cos 45o = 1.
Do đó = 1.
Lời giải:
Ta có
3 . 8 .
= 45o.
Vậy góc giữa hai vectơ và bằng 45°.
Lời giải:
Do vật dịch chuyển cùng hướng với nên góc tạo bởi vectơ hướng di chuyển của vật và bằng 0o.
Khi đó công sinh bởi lực bằng:
20 . 50 . cos 0o = 1 000 J.
Vậy công sinh bởi lực bằng 1 000 J.
3. Tính chất của tích vô hướng
Thực hành 4 trang 101 Toán lớp 10 Tập 1: Cho hai vectơ vuông góc, cùng có độ dài bằng 1.
b) Cho . Tính tích vô hướng và tính góc .
Lời giải:
Do hai vectơ vuông góc nên .
a) Ta có = 12 + 2 . 1 . 1 + 12 = 4.
= 12 - 2 . 1 . 1 + 12 = 0.
= 12 - 12 = 0.
b) ; .
Do đó = 6 . 0 = 0.
Khi đó cos = 0 (do > 0 và > 0).
= 180o.
Lời giải:
Do nên .
Ta có
= 1,62 + 2 . 1,6 . 1,6 . cos 120o + 1,62
= 2,56
Do đó = 1,6.
Vậy độ dài của bằng 1,6 đơn vị.
Bài tập
Lời giải:
AC là độ dài cạnh huyền của tam giác vuông cân có cạnh bằng a nên
AC = .
Do ABCD là hình vuông nên AC = BD = .
Do AB AD nên do đó = a . a = a2.
Do đó = a2.
Tam giác ABC vuông cân tại B nên = 45o.
= a . . cos = a2 . cos 45o = a2.
Do đó = a2.
= - . a . cos = a2 . cos 45o = -a2.
Do đó = -a2.
Do ABCD là hình vuông nên AC BD.
Do đó nên = 2a2.
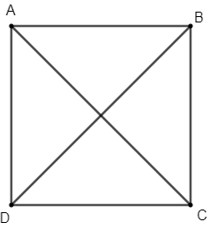
Bài 2 trang 101 Toán lớp 10 Tập 1: Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:
Lời giải:
a) AC là độ dài cạnh huyền của tam giác vuông có độ dài hai cạnh lần lượt là 2a và a.
Do đó AC = (do AC là độ dài đoạn thẳng nên AC > 0).
Hình chữ nhật ABCD có tâm O nên O là trung điểm của AC.
Do đó AO = AC = .
Tam giác ABC vuông tại B nên .
= 30o
= 2a . . cos = = 2a . . = a2.
Vậy .
b) Do AB AD nên do đó = 2a . a = 2a2.
a) Điểm O nằm ngoài đoạn thẳng AB;
b) Điểm O nằm trong đoạn thẳng AB.
Lời giải:
a)

Do O nằm ngoài đoạn thẳng AB nên hai vectơ và cùng hướng.
Do đó = 0o.
Khi đó = a . b . cos 0o = a.b.
b)

Do O nằm trong đoạn thẳng AB nên hai vectơ và ngược hướng.
Do đó = 180o.
Khi đó = a . b . cos 180o = -a.b.
Lời giải:
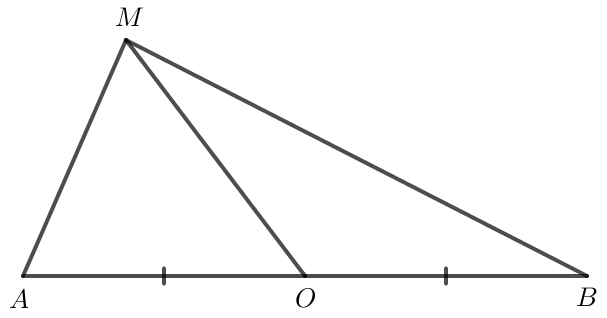
Do O là trung điểm của AB nên .
Khi đó
= MO2 - OA2.
Vậy = MO2 - OA2.
Lời giải:
Công sinh bởi lực bằng: 90 . 100 . cos 60o = 4 500 J.
Vậy công sinh bởi lực bằng 4 500 J.
Lời giải:
Gọi hai vectơ đó lần lượt là và .
Khi đó ta có = -6.
3 . 4 . = -6
= 120o.
Vậy góc giữa hai vectơ đó bằng 120o.